
- •2010 Г.
- •Глава 1. Элементы математической логики и теории
- •Глава 2. Элементы линейной алгебры
- •Глава 3. Векторная алгебра
- •Глава 4. Аналитическая геометрия на плоскости
- •Глава 5. Аналитическая геометрия в пространстве
- •Глава 1. Элементы математической логики и теории множеств
- •1.1. Аксиоматический метод
- •1.2. Алгебра высказываний
- •1.3. Логика предикатов
- •1.4. Множества и их элементы
- •1.5. Операции над множествами
- •1.6. Отображения множеств
- •1.7. Мощность множества
- •Глава 2. Элементы линейной алгебры
- •2.1. Системы линейных уравнений
- •2.2. Матрицы и действия над ними
- •2.3. Запись систем в матричной форме и их решение
- •2.4. Определители и их свойства
- •2.5. Правило Крамера
- •2.6. Решение системы линейных уравнений снеизвестными методом Гаусса
- •2.7. Теорема Кронекера-Капелли
- •2.8. Обратная матрица
- •2.9. Векторное пространство
- •Глава 3. Векторная алгебра
- •3.1. Система координат на прямой, на плоскости и в пространстве
- •3.2. Векторы и линейные операции над ними
- •3.3. Скалярное произведение векторов
- •3.4. Векторное произведение двух векторов
- •3.5. Смешанное произведение трех векторов
- •Глава 4. Аналитическая геометрия на плоскости
- •4.1. Уравнение линии в заданной системе координат
- •4.2. Различные формы уравнения прямой на плоскости
- •4.3. Основные задачи на прямую на плоскости
- •4.4. Окружность
- •4.5. Эллипс
- •4.6. Гипербола
- •4.7. Парабола
- •4.8. Классификация кривых второго порядка
- •4.9. Построение эллипса, гиперболы, параболы
- •4.10. Кривые второй степени и конические сечения
- •Глава 5. Аналитическая геометрия в пространстве
- •5.1. Поверхности и линии в пространстве
- •5.2. Уравнение плоскости в пространстве
- •5.3. Основные задачи о положении плоскости
- •5.4. Уравнения прямой в пространстве
- •5.5. Основные задачи о положении прямой
- •5.6. Задачи на взаимное расположение прямой и плоскости
- •5.7. Цилиндрические и конические поверхности
- •5.8. Поверхности вращения
- •5.9. Технические приложения геометрических свойств поверхности
Глава 3. Векторная алгебра
В последнем параграфе предыдущей главы мы познакомились с n-мерными линейными и евклидовыми пространствами. Важнейшими для практических приложений частными случаями n-мерных евклидовых пространств являются прямая, плоскость, трехмерное пространство, снабженные декартовыми системами координат. В этой главе мы будем изучать двух и трехмерные линейные пространства, элементами которых являются направленные отрезки, называемые векторами. Заметим, что исторически сначала в науке, исходя из запросов механики и физики возникло именно такое понятие вектора, и лишь потом с развитием линейной алгебры на безе представлений о векторе как о направленном отрезке воз-
никли понятия линейного и евклидового пространства.
3.1. Система координат на прямой, на плоскости и в пространстве
Разговор о векторах, как о направленных отрезках, начнем с обсуждения понятия отрезка и его длины.
Эти
понятия известны из элементарной
геометрии. Отрезок есть часть прямой,
ограниченная двумя точками. Длина
отрезка есть положительное число,
получаемое измерением этого отрезка с
помощью некоторого заранее выбранного
отрезка - единицы масштаба. Отрезок,
ограниченный точками
 и
и будем обозначать
AB или BA, его длину - │AB│ или │BA│.
будем обозначать
AB или BA, его длину - │AB│ или │BA│.
В математике, механике, физике часто важнейшую роль играет направление отрезка. Например, это принципиально важно, если с помощью отрезка характеризовать скорость движения материальной точки или силу, действующую на нее.
Чтобы охарактеризовать направление отрезка, одну из двух ограничивающих его точек принимают за начало отрезка, а другую - за его конец; направлением отрезка считают направление от начала к концу. Отрезок, на котором указано направление (т.е. сказано, какая из двух граничных точек считается началом и какая - концом) называется направленным отрезком или вектором.
Обозначать
направленный отрезок с началом в точке
 и концом в
точке
и концом в
точке будем
будем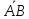 .
Заметим, что направленные отрезки
.
Заметим, что направленные отрезки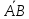 и
и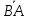 различны так, как их направления
противоположны.
различны так, как их направления
противоположны.
Если рассматривать направленные отрезки, расположенные на одной прямой, то их направления можно характеризовать знаками + и -. Для этого одно из них (все равно какое) назовем положительным, а другое - отрицательным. Положительное направление на чертеже будем отмечать стрелкой (на рисунке 3.1 направление слева направо принято за положительное).

Рис.3.1. Ось.
Прямая, на которой выбрано положительное направление называется осью.
Длина
направленного отрезка, расположенного
на оси, взятая с определенным знаком,
называется величиной
направленного отрезка оси
(в дальнейшем для краткости часто вместо
направленный отрезок оси будем говорить
отрезок
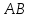 );
при этом знак выбирается положительным,
если направление отрезка совпадает с
положительным направлением оси;
отрицательным - в противном случае.
Так, величина направленного отрезка
);
при этом знак выбирается положительным,
если направление отрезка совпадает с
положительным направлением оси;
отрицательным - в противном случае.
Так, величина направленного отрезка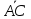 положительна, а величина отрезка
положительна, а величина отрезка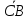 - отрицательная (рис.3.1). Очевидно, что
длина направленного отрезка равна
модулю его величины. Условимся
длину направленного отрезка
- отрицательная (рис.3.1). Очевидно, что
длина направленного отрезка равна
модулю его величины. Условимся
длину направленного отрезка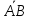 обозначать
обозначать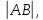 а его величину - символомвел(AB).
а его величину - символомвел(AB).
В дальнейшем нам потребуется и такой направленный отрезок, начало и конец которого совпадают. Направление этого отрезка можно выбирать произвольно. Длина, а следовательно и его величина равны нулю. Такие отрезки мы будем называть нулевыми.
Возьмем
на некоторой оси три точки
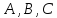 и выясним, чему равна сумма величин
направленных отрезков
и выясним, чему равна сумма величин
направленных отрезков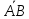 и
и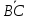 .
.
При любом расположении точек A,B,C на оси сумма величин
направленных
отрезков 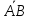 и
и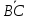 равнавел
равнавел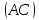 :
:
вел(AB) + вел(BC) = вел(AC), (3.1)
(т.е. сумма величин направленных отрезков, расположенных на оси так, что конец первого из них является началом второго, равна величине отрезка, у которого начало совпадает с началом первого из указанных отрезков, а конец - с концом второго из них).
Замечание 3.1. Если бы в равенстве (3.1) стояли бы не величины, а длины направленных отрезков, то оно было бы справедливо только в том случае, когда точка B лежит на отрезке AC и теряло бы силу при любом другом расположении точек.
Пользуясь
равенством (3.1), легко показать, что при
любом числе точек
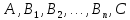 и произвольном их расположении на оси
мы будем иметь:
и произвольном их расположении на оси
мы будем иметь:
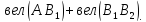 +…+
+…+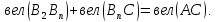
Посмотрим, как можно определить положение точки на прямой.
Возьмем на рассматриваемой прямой некоторую точку О (от латинского origo - начало), относительно которой будем определять положение всех остальных точек прямой. Ясно, что положение любой точки P, лежащей на этой прямой, будет вполне определяться направленным отрезком OP, так как каждой точке прямой соответствует определенный направленный отрезок с началом в точке O и концом в рассматриваемой точке P, и, обратно, каждому направленному отрезку с началом в точке O соответствует единственная точка P, являющаяся концом этого отрезка.
Установим теперь на рассматриваемой прямой положительное направление и выберем единицу масштаба m (на рис.3.2 положительное направление выбрано слева направо). Тогда положеие
 Рис.
3.2. Прямая с системой координат
Рис.
3.2. Прямая с системой координат
любой точки P на прямой можно будет задать величиной направленного отрезка оси OP. Это число, определяющее положение точки, называется ее координатой. Итак, величина направленного отрезка OP является координатой точки P на прямой линии. Обозначая координату точки P буквой x, имеем: x = вел (OP). Обратно, по заданной координате x можно построить единственную точку: она будет концом направленного отрезка, соединяющего точку O с точкой P, величина которого равна x.
Если на прямой отмечена некоторая точка O, указано положительное направление и, кроме того, выбрана единица масштаба, то мы будем говорить, что на прямой установлена система координат. Точка O, являющаяся началом рассматриваемых направленных отрезков, называется началом координат, а данная прямая осью координат.
В тексте условимся координату точки писать в скобках рядом с буквой, обозначающей эту точку: P(x).
Дадим теперь понятие о методе координат на плоскости, т.е. укажем способ, позволяющий определять положение точки на плоскости с помощью чисел.

Рис. 3.3. Система координат на плоскости
Возьмем две взаимно перпендикулярные прямые и на каждой из них установим положительное направление. В качестве начала координат на каждой из них возьмем точку их пересечения. Оси обычно располагают так, как это указано на рисунке 3.3: одну из них горизонтально и положительное направление на ней выбирают слева направо, а другую - вертикально и положительное направление на ней - снизу вверх. Одна из осей (обычно горизонтальная) называется осью абсцисс (ось Ox), а другая - осью ординат (ось Oy). Точка пересечения осей называется началом координат. На рисунке 3.3 начало координат обозначено буквой O. Выберем единицу масштаба (мы всегда будем предполагать, что на обеих осях координат выбрана одна и та же единица масштаба). Теперь мы можем сказать, что на плоскости установлена система координат. Оси абсцисс и ординат называются осями координат.
Положение любой точки на плоскости, имеющей систему координат, можно определить числами - координатами этой точки. Действительно, каждой точке M плоскости соответствуют на осях координат две точки P и Q, являющиеся ее проекциями на эти оси и наоборот, зная точки P и Q на осях координат, можно построить единственную точку M на плоскости, для которой P и Q являются проекциями на эти оси. Проекцией точки M на ось называется основание перпендикуляра, опущенного из M на эту ось.
Проекцией
отрезка 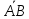 на ось
на ось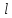 ,
называется величина отрезка
,
называется величина отрезка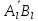 ,
где
,
где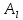 и
и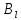 - проекции точек A и B на ось
- проекции точек A и B на ось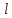 ,
обозначать такую проекцию будем
,
обозначать такую проекцию будем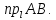
Таким
образом, определение положения точки
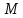 на плоскости сводится к определению
положения ее проекций
на плоскости сводится к определению
положения ее проекций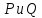 на координатные оси. Но мы уже знаем,
что положение точки на оси координат
вполне определяется ее координатой.
Пусть
на координатные оси. Но мы уже знаем,
что положение точки на оси координат
вполне определяется ее координатой.
Пусть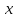 – координата точки
– координата точки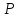 на оси абсцисс (
на оси абсцисс (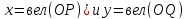 - координата точки Q на оси ординат.
Числа
- координата точки Q на оси ординат.
Числа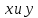 полностью определяют положение точки
полностью определяют положение точки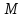 на плоскости и называютсякоординатами
точки,
при этом
на плоскости и называютсякоординатами
точки,
при этом
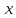 называетсяабсциссой
точки
называетсяабсциссой
точки
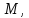 y - ординатой.
y - ординатой.
Абсциссой
точки
называется величина направленного
отрезка оси
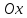 ,
началом которого является начало
координат, а концом - проекция точки на
эту ось;ординатой
точки
называется величина направленного
отрезка оси
,
началом которого является начало
координат, а концом - проекция точки на
эту ось;ординатой
точки
называется величина направленного
отрезка оси
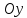 ,
началом которого является начало
координат, а концом проекция точки на
ось ординат.
,
началом которого является начало
координат, а концом проекция точки на
ось ординат.
Координаты
точки условимся писать в скобках рядом
с буквой, обозначающей эту точку, ставя
на первое место абсциссу точки и на
второе - ее ординату и разделяя их точкой
с запятой:
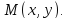 Начало
координат имеет нулевые абсциссу и
ординату.
Начало
координат имеет нулевые абсциссу и
ординату.
Оси
координат делят плоскость на четыре
части, называемые четвертями или
квадрантами. Часть плоскости,
заключенная между положительными
полуосями
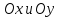 называется первым квадрантом. Дальше
нумерация квадрантов идет против
часовой стрелки.
называется первым квадрантом. Дальше
нумерация квадрантов идет против
часовой стрелки.
Рассмотренная система координат называется прямоугольной, или декартовой, по имени математика и философа Декарта, заложившего в 1637 году основы аналитической геометрии.
Из описанного метода координат вытекает решение двух основных задач.
1. По данной точке найти ее координаты. Решение этой задачи подробно было рассмотрено ранее.
2.
Зная координаты
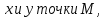 построить эту точку. Отложим по оси
построить эту точку. Отложим по оси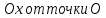 отрезок длиной
отрезок длиной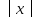 единиц вправо, если
единиц вправо, если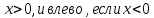 .
Конец этого отрезка -
.
Конец этого отрезка -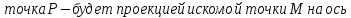 абсцисс. По оси ординат откладываем от
точки
абсцисс. По оси ординат откладываем от
точки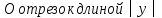 единиц (в соответствующую сторону),
получим точку
единиц (в соответствующую сторону),
получим точку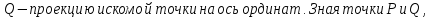 легко построить по ним как по проекциям
искомую точку
легко построить по ним как по проекциям
искомую точку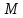 .
.
Для определения положения точки на плоскости кроме декартовой часто используется полярная система координат.
Рассмотрим
на плоскости некоторую точку
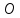 (назовем ееполюсом)
и проходящую через нее ось
(назовем ееполюсом)
и проходящую через нее ось
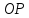 (полярную
ось).
Пусть на этой оси указана единица
масштаба.
(полярную
ось).
Пусть на этой оси указана единица
масштаба.
Полярным
радиусом
точки плоскости
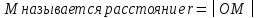 от нее до полюса,полярным
углом точки
от нее до полюса,полярным
углом точки
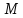 - угол
- угол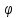 между полярной осью и направлением
отрезка
между полярной осью и направлением
отрезка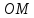 (рис. 3.4).
(рис. 3.4).
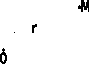
Рис.3.4. Полярная система координат
Условимся
угол 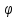 брать в пределах -
брать в пределах -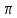 <
<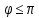 .
Тогда каждой точке плоскости соответствует
единственная пара чисел
.
Тогда каждой точке плоскости соответствует
единственная пара чисел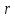 ,
,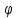 (исключением является полюс, для которого
(исключением является полюс, для которого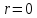 ,
а
,
а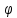 -
любое). Обратно, каждой паре чисел
-
любое). Обратно, каждой паре чисел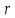 и
и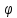 (
(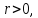 -
-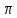 <
<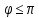 ) соответствует единственная точка
плоскости, для которой
) соответствует единственная точка
плоскости, для которой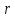 является
полярным радиусом, а
является
полярным радиусом, а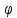 - полярным углом. Полярный радиус и
полярный угол будем называтьполярными
координатами.
Записывать их будем в скобках после
буквы, обозначающей точку:
- полярным углом. Полярный радиус и
полярный угол будем называтьполярными
координатами.
Записывать их будем в скобках после
буквы, обозначающей точку:
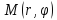 .
.
Установим
связь между декартовыми и полярными
координатами одной и той же точки.
Совместим полюс полярной системы с
началом координат декартовой, а полярную
ось направим по оси абсцисс (рис. 3.5).
Пусть точка
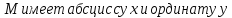 ,
а ее полярные координаты равны
,
а ее полярные координаты равны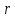 и
и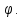
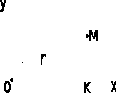
Рис.3.4. Связь между полярной и декартовой системами координат
Из
прямоугольного треугольника OKM найдем
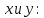
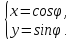 (3.2)
(3.2)
Формулы (3.2) выражают декартовые координаты точки через ее полярные координаты.
Найдем полярные координаты точки, зная ее декартовы координаты. По теореме Пифагора из треугольника OKM находим, что
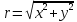 (3.3)
(3.3)
Из равенств же (3.2) получаем:
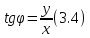
По
формуле (3.4) определяется тангенс
полярного угла 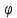 ,
при этом для него получаются два
значения (напомним, что -
,
при этом для него получаются два
значения (напомним, что -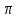 <
<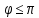 ), лежащие в разных четвертях. Так как
), лежащие в разных четвертях. Так как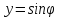 ,
то из этих двух значений надо выбрать
то, для которого синус имеет тот же
знак, что и
,
то из этих двух значений надо выбрать
то, для которого синус имеет тот же
знак, что и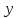 .
.
Пример
3.1.
Найти полярные координаты точек
M(1;-1) и N(-1;1). Эти точки имеют одинаковые
полярный радиусы
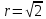 и тангенс полярного угла, равный -1. В
интервале от -
и тангенс полярного угла, равный -1. В
интервале от -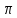 <
<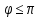 тангенс равен -1 при
тангенс равен -1 при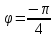 и
и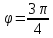 .
Итак, полярные координаты точки M:
.
Итак, полярные координаты точки M: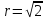 ,
,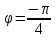 ;
точки N:
;
точки N: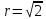 ,
,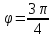 .
.
Вводя
полярные координаты, мы предполагали,
что r>0 и - 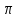 <
<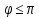 .
В дальнейшем мы будем считать что
полярные координаты могут принимать
любые значения от
.
В дальнейшем мы будем считать что
полярные координаты могут принимать
любые значения от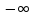 до
до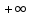 .
В этом случае построение точки по ее
полярным координатам условимся
производить следующим образом.
.
В этом случае построение точки по ее
полярным координатам условимся
производить следующим образом.
Проведем
через полюс O ось под углом 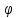 к полярной оси (делая в случае
необходимости несколько полных оборотов)
и отложим от полюса отрезок OM длиною
│r│ в положительном направлении
построенной оси, если r>0, и в отрицательном
при r<0. Конец M этого отрезка и
будет искомой точкой. Отметим, что
формулы (3.2) остаются справедливыми и
для рассмотренного случая. При нахождении
r по формуле (3.3) радикал можно брать с
любым знаком, причем
к полярной оси (делая в случае
необходимости несколько полных оборотов)
и отложим от полюса отрезок OM длиною
│r│ в положительном направлении
построенной оси, если r>0, и в отрицательном
при r<0. Конец M этого отрезка и
будет искомой точкой. Отметим, что
формулы (3.2) остаются справедливыми и
для рассмотренного случая. При нахождении
r по формуле (3.3) радикал можно брать с
любым знаком, причем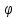 выбирается так, чтобы
выбирается так, чтобы имел тот же знак, что и
имел тот же знак, что и так
как
так
как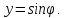
Подобно случаю для плоскости, вводится прямоугольная система координат в пространстве.
Проведем через некоторую точку O пространства три взаимно перпендикулярных оси Ox, Oy, Oz оси координат, относительно которых будем определять положение точек пространства. Оси координат обычно располагают так как это указано на рисунке 3.6а (правая система координат):

Рис.3.6а. Декартова система координат в пространстве.
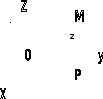
Рис.3.6б. Цилиндрическая система координат.
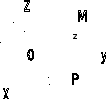
Рис.3.6б. Сферическая система координат.
ось Ox (абсцисс) горизонтально вперед (в сторону читателя), ось Oy (ординат) горизонтально слева направо, ось Oz (аппликат) вертикально снизу вверх. Теперь положение любой точки пространства можно задать тремя числами - ее координатами: проекциями точки на координатные оси.
Наряду с рассмотренной прямоугольной системой координат в пространстве иногда используются цилиндрическая и сферическая системы координат.
Цилиндрические
координаты
представляет собой соединение полярных
координат с обычной декартовой
осью аппликат (рис.3.6б). Координатами
точки M в этой системе являются числа
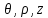 ,
где
,
где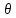 и
и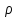 полярные координаты проекции точки M
на плоскость Oxy и z - аппликата точки M.
Формулы, связывающие цилиндрические
координаты с декартовыми имеют вид:
полярные координаты проекции точки M
на плоскость Oxy и z - аппликата точки M.
Формулы, связывающие цилиндрические
координаты с декартовыми имеют вид:
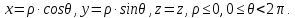
Сферические координаты связаны с декартовыми формулами:
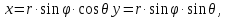 x=r
x=r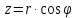 ,
,
где
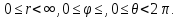
Геометрический
смысл сферических координат должен
быть ясен из рисунка 3.6в: r есть радиус-вектор
OM, соединяющий начало (полюс) с данной
точкой M; 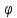 - угол, образуемый этим радиусом-вектором
с осью Oz (полярной осью);
- угол, образуемый этим радиусом-вектором
с осью Oz (полярной осью);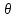 - угол, составляемый с осью Ox проекцией
OP=
- угол, составляемый с осью Ox проекцией
OP=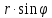 радиуса-вектора OM на плоскость Oxy
(перпендикулярную к полярной оси).
радиуса-вектора OM на плоскость Oxy
(перпендикулярную к полярной оси).
Отметим,
не вдаваясь в подробности, что так же
как и в случае с полярной системой
координат на плоскости (там при 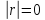 угол
угол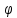 мог
принимать любые значения) для рассмотренных
цилиндрической и сферической систем
координат нарушается взаимная
однозначность их соответствия декартовой
системе. Но это, как правило, не мешает
использовать рассмотренные системы
при решении практических задач.
мог
принимать любые значения) для рассмотренных
цилиндрической и сферической систем
координат нарушается взаимная
однозначность их соответствия декартовой
системе. Но это, как правило, не мешает
использовать рассмотренные системы
при решении практических задач.
Остановимся на вопросе о переходе от одной декартовой системы координат в пространстве к другой.
1.
Рассмотрим две системы координат Oxyz и
O'xyz, отличающиеся только своим началом
(соответствующие координатные оси этих
систем имеют одинаковые направления
и масштабы). Пусть начало координат O'
системы O'xyz имеет координаты
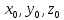 в системе Oxyz.
в системе Oxyz.
Если
точка M в системе Oxyz имеет координаты
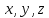 ,
то в системе O'xyz она будет иметь координаты
,
то в системе O'xyz она будет иметь координаты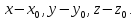
2. Пусть системы координат Oxyz и O'xyz имеют одинаковое начало и пусть направления их соответствующих осей совпадают. Если одна единица масштаба системы Oxyz содержит b единиц масштаба системы O'xyz, и точка M имеет в системе Oxyz координаты x, y, z, то в системе O'xyz эта точка будет иметь координаты bx, by, bz (мы здесь предполагаем, что для всех осей системы выбраны одинаковые единицы масштаба).
3. В общем случае для перехода от одной системы координат к другой надо знать координаты направляющих ортов одной системы в другой. Пусть i, j, k - направляющие орты координатных осей системы Oxyz, i', j', k' - направляющие орты в системе O'xyz. Пусть
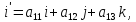
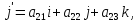
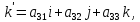
Если в системе O'xyz точка M имеет координаты (x',y',z'), то с системе Oxyz ее координаты (x,y,z) определяются по формулам:
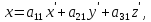
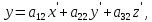
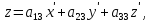
Если обозначит
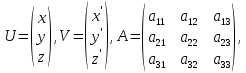
то
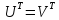 ,
отсюда
,
отсюда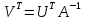 .
.
