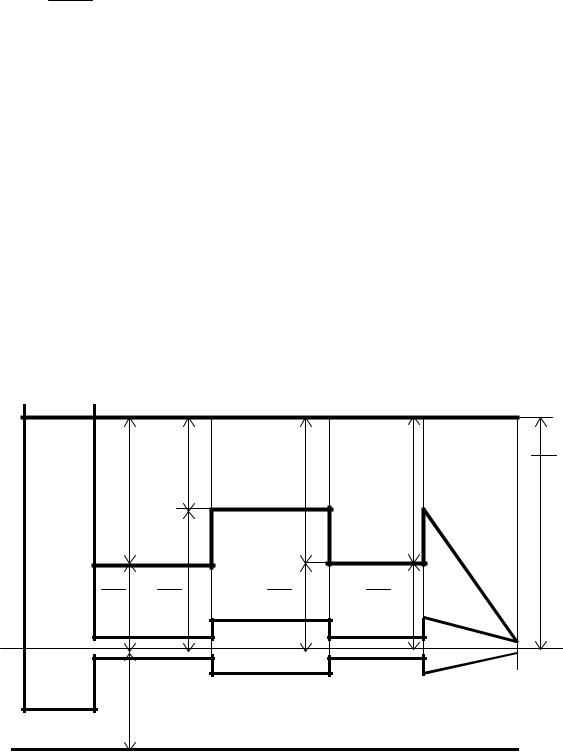
Рис.13 . Диаграмма Бернулли для потока идеальной жидкости

-33-

Принципы построения те же, что и для струйки идеальной жидкости, с учетом дополнительного слагаемого h1-2 в правой части уравнения.

¾Для всех сечений геометрический напор постоянен и равен z1. Если горизонтальная плоскость отсчета потенциальной энергии положения 0-0 совпадает с осью трубы, все z=0. Расстояние от оси трубы до пьезометрической линии равно пьезометрическому напору р/ρg, здесь под давлением р подразумевается манометрическое давление. Расстояние от пьезометрической линии до напорной равно скоростному напору ϑ2/2g.

¾В начальном сечении н-н скорость равна нулю, манометрическое давление равно нулю и полный напор равен геометрическому - высоте жидкости в сосуде. Полный напор постоянен по всей длине трубы и напорная линия горизонтальна.

¾Пусть известна скорость в сечении 1 и равна ϑ1. Отложим вниз от напорной линии в масштабе графика скоростной напор ϑ12/2g (отрезок ab) и получим пьезометрический напор в этом сечении р1/ρg. При постоянном диаметре на участке трубы между сечениями 1 и 2 скорость и скоростной напор, и, следовательно, р/ρg сохраняют постоянное значение. Этому будет соответствовать участок пьезометрической линии в виде горизонтальной прямой bc.

¾В сечении 2 в связи с резким увеличением диаметра трубы скорость резко уменьшается, а давление резко возрастает (уменьшение скорости в горизон-

тальной трубе приводит к увеличению давления - следствие из уравнения Бернулли!). Поэтому пьезометрическая линия здесь резко возрастает - участок cd, далее до сечения 3 изображается горизонтальной прямой de (диаметр трубы не меняется!).

¾В сечении 3 диаметр трубы резко уменьшается и все происходит наоборот: скорость возрастает, давление падает и пьезометрическая линия круто опускается вниз (участок ef).

¾Между сечениями 3 и 4 пьезометрическая линия изображается горизонтальной прямой (участок fg). В сечении 4 диаметр трубы резко возрастает и на участке 4-5 постепенно уменьшается. При этом давление в сечении 4 резко возрастает ( пьезометрическая линия имеет скачок вверх gh. далее абсолютное давление постепенно снижается до атмосферного, а манометрическое до нуля. Конечная точка k пъезометрической линии лежит на оси трубы.

Принципы построения диаграммы для реальной жидкости

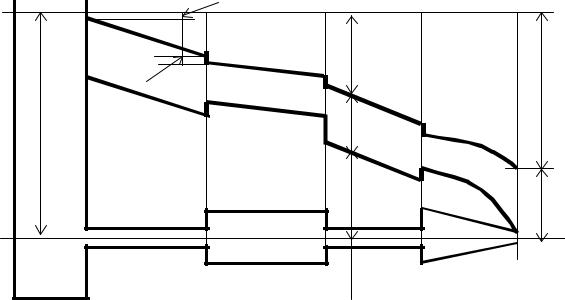
¾Первой строится напорная линия. В начальном сечении н-н напор равен: H=z+p/ρg+ϑ2/2g=H0+0+0=H0 - высоте уровня жидкости в резервуаре. Здесь под давлением р понимается манометрическое давление. В сечении 1 отложим от уровня жидкости вертикально вниз отрезок ab, равный потере напора на входе в трубу ( это местные потери в сечении1). На участке трубы между сечениями 1 и 2 имеет место потеря напора на трение по длине. Пусть она

равна hдл1-2. Тогда для получения точки напорной линии в конце участка 1-2 вычитаем из напора HB эту величину и получаем точку с. Так как диаметр

-34-

трубы на этом участке постоянен, угол наклона напорной линии к горизонту тоже будет постоянным (угол наклона ~ скорости движения). Напорная линия на этом участке будет иметь вид прямой линии bc. Аналогично: в сечениях 3 4 напорная линия имеет скачки вниз на величину местных потерь, на участках постоянного диаметра 2-3 и 3-4 напорная линия имеет вид наклонных прямых ce и fg. На участке 4-5 диаметр трубы увеличивается и скорость к концу трубы возрастает. Это приводит к увеличению потерь на трение и напорная линия имеет вид кривой gm.

¾Пьезометрическая линия - построение начинается с конца трубы. Так как манометрическое давление в точке k равно нулю, это и будет начальная точка пьезометрической линии. Величина km равна скоростному напору в сечении 5. Далее идем справа налево по трубе и из ординат напорной линии вычитаем отрезки, соответствующие скоростным напорам. Соотношение между скоростными напорами (или скоростями) определяется из уравнения постоянства расхода. Там, где диаметр трубы больше, скорость меньше и наоборот. На участках 1-2, 2-3 и 3-4 скорости по длине не меняются. При этом напорная и пьезометрическая линии параллельны.

abcdefghm - напорнаялиния

Рис.14. Диаграмма Бернулли для реальной жидкости