Гидравлика для студентов / метод.указ по гидродинамике

12.Почему с увеличением расхода жидкости любая гидравлически гладкая труба становится гидравлически шероховатой?

13.Почему с уменьшением расхода жидкости любая гидравлически шероховатая труба становится гидравлически гладкой?

14.Почему при ламинарном режиме потери напора на трение по длине пропорциональны скорости в первой степени?

15.Почему при развитом турбулентном режиме (Re>105) потери напора на трение по длине пропорциональны скорости во второй степени?

41

5 ЛАБОРАТОРНАЯ РАБОТА № 4 «ПОТЕРИ НАПОРА НА ВНЕЗАПНОМ РАСШИРЕНИИ»

Местные сопротивления вызываются фасонными частями, арматурой и другим оборудованием трубопроводных, сетей, которые приводят к изменению величины или направления скорости движения жидкости на отдельных участках трубопровода (при расширении или сужении потока, в результате его поворота, при протекании потока через диафрагмы, задвижки и т. д.), что всегда связано с появлением дополнительных потерь напора.

В водопроводных магистральных трубах потери напора на местные сопротивления обычно весьма невелики (не более 10— 20% потерь напора на трение). В воздухопроводах вентиляционных и пневмотранспортных установок, в дутьевых установках котельных потери на преодоление местных сопротивлений часто значительно больше потерь напора на трение. Местные сопротивления являются весьма существенными и при расчете паро-

проводов.

Потери напора, затраченного на преодоление какого-либо местного сопротивления, принято оценивать в долях скоростного напора, соответствующего скорости непосредственно за рассматриваемым местным сопротивлением, т. е. определять их из формулы Вейсбаха:

hм 2

2 g

где — так называемый коэффициент местного сопротивления.

Коэффициенты разных местных сопротивлений находят, как правило, опытным путем; таблицы значений этих коэффициентов (или эмпирические кривые и формулы для них) содержатся во всех инженерных справочниках и руководствах по гидравлике. Для некоторых практически важных случаев значения коэффициентов местных сопротивлений удалось получить также теоретическим путем.

Иногда местные потери напора выражают в виде эквивалентной длины lэ прямого участка трубопровода, сопротивление трения которого по величине равно рассматриваемым местным потерям напора, т. е. из условия

или

42

Коэффициент гидравлического трения , как уже было выяснено, зависит от числа Рейнольдса и относительной шероховатости, поэтому одному и тому же значению

эквивалентная длина заданного местного сопротивления постоянна.

Основные виды местных потерь напора можно условно разделить на следующие группы:

-потери, связанные с изменением сечения потока (или, что то же, его средней скорости). Сюда относятся случаи внезапного расширения, сужения, а также постепенного расширения и сужения потока;

-потери, вызванные изменением направления потока. Сюда относятся различного рода колена, угольники, отводы, используемые на трубопроводах;

-потери, связанные с протеканием жидкости через арматуру различного типа (вентили,

краны, обратные клапаны, сетки, отборы, дроссель-клапаны и т. д.);

- потери, связанные с отделением одной части потока от другой или слиянием двух потоков в один общий. Сюда относятся, например, тройники, крестовины и отверстия в боковых стенках трубопроводов при наличии транзитного расхода.

5.1 Внезапное расширение трубопровода. Вывод теоремы Борда.

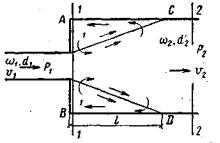
Рассмотрение местных сопротивлений целесообразно начать со случая, который часто встречается на практике, когда трубопровод внезапно расширяется от диаметра d1 до диаметра d2 (рисунок 5.1).

Рисунок 5.1 – К выводу теоремы Борда Как показывают наблюдения, поток, выходящий из узкой трубы, не сразу заполняет все

поперечное сечение широкой трубы; жидкость в месте расширения отрывается от стенок и дальше движется в виде свободной струи, отделенной от остальной жидкости поверхностью

43

раздела. Поверхность раздела неустойчива, на ней возникают вихри, в результате чего транзитная струя перемешивается с окружающей жидкостью. Струя постепенно расширяется,

пока, наконец, на некотором расстоянии l от начала расширения не заполняет все сечение ши-

рокой трубы.

В кольцевом пространстве между струей и стенками трубы жидкость находится в вихревом движении: жидкость из этой зоны вовлекается в центральную струю; с другой стороны, жидкость из центральной струи попадает в вихревую зону. Благодаря отрыву потока и связанному с ним вихреобразованию на участке трубы между сечениями 1 и 2

теряются значительные потери напора.

Найдем величину этих потерь. Обозначим средние скорости потока в сечениях 1 и 2 через и

υ1 и υ2 , а давления — через р1 и р2. Давление на торцовой стенке АВ, как показывает опыт,

практически равно давлению на выходе из узкой части трубы, т. е. р1.

По уравнению Бернулли потери напора между сечениями 1 и 2 равны (если положить

α1= α2 1):

Из теоремы импульсов для тех же двух сечений можно получить

Из теоремы импульсов для тех же двух сечений можно получить

или

44

h1 2 ( 1 2 )2 (5.5)

Отсюда следует, что потери напора при внезапном расширении равны скоростному напору от потерянной скорости. Этот результат называется теоремой или формулой Борда.

Формулу (5.5) можно привести к виду

Таким образом, в рассматриваемом случае

Если отнести коэффициент местного сопротивления к скорости в широкой трубе, то

где

Формула (5.6) хорошо подтверждается опытами в случае турбулентного движения,

если сечение 2 берется достаточно далеко за местом расширения, т. е. там, где устанавливается нормальное распределение скоростей по сечению.

5.2 Проведение лабораторной работы

Цель: экспериментальное изучение закономерностей потерь напора и распределения давлений в местных сопротивлениях.

Лабораторная работа проводится на модуле М2 «Потери напора на внезапном расширении» (приложение А).

Порядок выполнения измерений:

1.Перейти от показаний ротаметров к расходу жидкости (смотри градуировочную характеристику ротаметров приложение Б);

2.Включить насос Н1 на панели управления (смотри рисунок 1.1);

3.Установить необходимый расход с помощью вентиля В2, В1 и выходного вентиля модуля В4 (смотри рисунок 1.2);

4.При достижении установившегося режима снять показания по ротаметрам Р1 и Р2 (приложение Б);

45

5. Произвести замеры по показаниям пьезометров (смотри рисунок 1.1).

Обработка опытных данных:

Расчетными соотношениями для определения коэффициента местного сопротивления по экспериментальным данным являются следующие. Применительно к рисунку, из уравнения Бернулли для сечения 1 и 2 следует:

где hвн.р – искомые потери на внезапном расширении.

Здесь сечение 2 выбирается на расстоянии достаточном для расширения потока на

Контрольные вопросы

1.Виды местных сопротивлений.

2.Вывод формулы Борда.

46

Список используемой литературы

1.Раинкина Л.Н., Санина Г.И. Определение коэффициента гидравлического трения:

Методические указания. –Ухта: УГТУ, 2000, - 25с.:, ил.

2.Раинкина Л.Н. Демонстрация уравнения Бернулли и его практическое применение:

Методические указания. – Ухта: УГТУ, 2002, - 36с., ил.

3.Альтшуль А.Д., Киселев П.Г. Гидравлика и аэродинамика (Основы механики жидкости). Учебное пособие для вузов. Изд. 2-е, перераб. и доп. М., Стройиздат, 1975. 323 с.

47

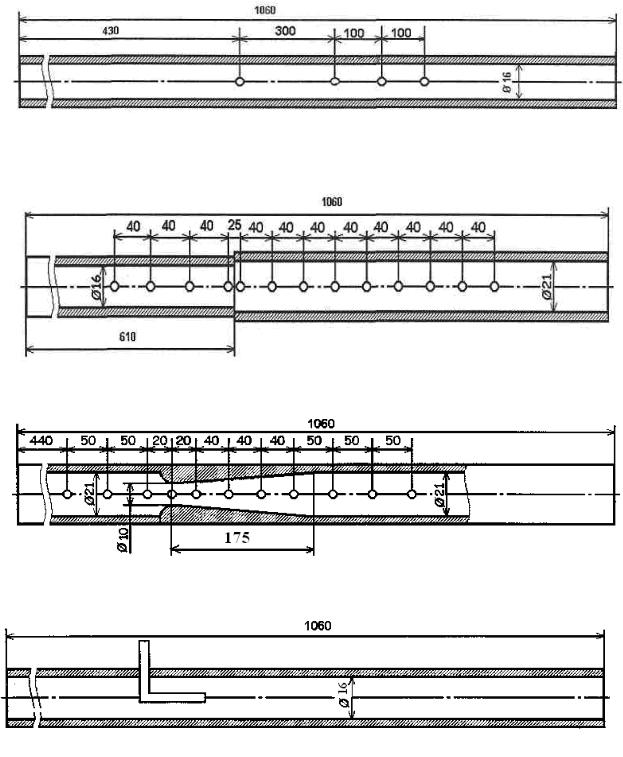
ПРИЛОЖЕНИЕ А

(справочное)

Геометрические характеристики модулей М1 «Потери напора по длине в круглой трубе»

М2 «Потери напора на внезапном расширении»

М3«Диаграмма Бернулли»

М4 «Режимы течения»

48

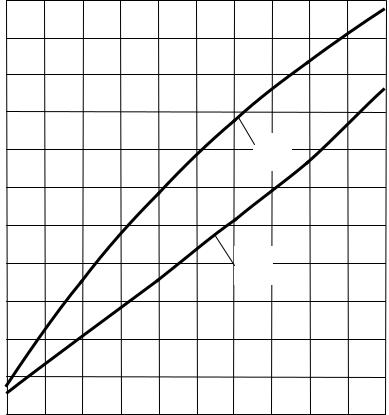
ПРИЛОЖЕНИЕ Б

Градуировка ротаметров

Q,

л/ч

1600

2

1200

400

Отметка шкалы

Для ротаметра № 558.8.85 (1)

Для ротаметра № 84.1.86 (2)

49

ПРИЛОЖЕНИЕ В

Значение эквивалентной шероховатости для различных труб

50