Гидравлика для студентов / метод.указ по гидродинамике

- показаний пьезометров Тр4 (смотри рисунок 1.1).

Обработка опытных данных.

1.Перейти от показаний ротаметров к расходу (смотри градуировочную характеристику ротаметров приложение Б).

2.По результатам измерений следует вычислить скорость в каждом i-ом сечении трубы Вентури:

где Q – расход, м3/с;

Si – площадь каждого i-го сечения трубы Вентури.

3. Вычислить скоростной напор в каждом i-ом сечении трубы Вентури.

где i - скорость в каждом i-ом сечении трубы Вентури, м/с; g – ускорение свободного падания, 9,81 м/с2.

Построение диаграммы Бернулли (построение выполнить на масштабно-

координатной бумаге):

1.Профиль трубы Вентури в масштабе (положение плоскости сравнения совпадает с осью трубы);

2.Пьезометрические напоры для каждого i-го сечения, откладывая их от оси трубы получить пьезометрическую линию;

3.Скоростные напоры, суммируя их с ординатами пьезометрической линии в соответствующих сечениях. Провести напорную линию;

4.Провести напорную плоскость (горизонтальную прямую) на уровне ординаты линии энергии первого пьезометра и обозначить потери напора

(энергии) между этим сечением и другим, расположенным ниже по течению

(по указанию преподавателя).

Результаты измерений и вычислений свести в таблицу 3.1, 3.2.

Таблица 3.1 - Результаты измерений

31

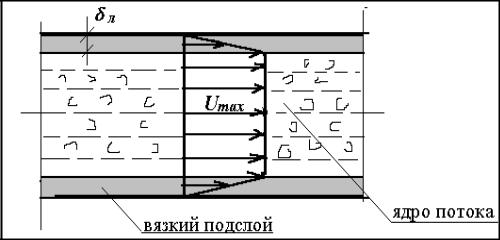
При движении жидкости по трубопроводу вблизи стенок скорость течения мала, а

на самой стенке равна нулю вследствие наличия сил межмолекулярного взаимодействия между жидкостью и твердым телом. Поэтому в пределах очень тонкого слоя,

примыкающего к стенке, развитие локальных возмущений, вызванных силами инерции,

становится невозможным. Здесь пульсационные перемешивания частиц не могут преодолеть сил вязкости жидкости и движение всегда остается ламинарным.

Следовательно, в турбулентном потоке не вся жидкость движется турбулентно. У

стенки всегда сохраняется тонкий пристенный слой, в котором жидкость движется ламинарно. Этот слой называется вязким подслоем и толщина его л измеряется долями миллиметра (рисунок 4.1).

Рисунок 4.1 - К понятию структуры турбулентного потока.

Толщина вязкого подслоя обратно пропорциональна числу Re и уменьшается с

возрастанием скорости движения жидкости.

Твердые стенки, ограничивающие поток жидкости, имеют неровности, которые называются шероховатостью. Она зависит от материала стенок и способа изготовления труб. В большинстве реальных трубопроводов шероховатость стенок неравномерная, что создает трудности при учете ее влияния на потери давления. В практику гидравлических расчетов вводится понятие “эквивалентная шероховатость” э. Это такая воображаемая равномерная шероховатость, при которой потери давления такие же,

как и для данной реальной шероховатости при прочих равных условиях. Значение э

определяется экспериментально и приводится в справочной литературе (приложение В).

На характер гидравлических сопротивлений оказывает существенное влияние соотношение между толщиной вязкого подслоя л и величиной эквивалентной шероховатости э. В гидравлике принято условно разделять трубы на гидравлически гладкие и гидравлически шероховатые.

34

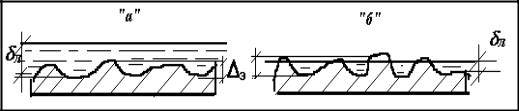
Если ламинарный подслой покрывает шероховатость, то есть л > э, такую трубу называют гидравлически гладкой (рисунок 4.2 ”а”). Ядро турбулентного потока при этом будет соприкасаться не с выступами шероховатости, а с ламинарным подслоем жидкости, скользя по его поверхности, как по гладкой трубе. В этом случае коэффициент гидравлического трения не зависит от шероховатости, скрытой в ламинарном подслое, а

зависит только от числа Re.

Если эквивалентная шероховатость больше толщины вязкого подслоя ( л < э), то такую трубу называют гидравлически шероховатой (рисунок 4.2 “б”).

Рисунок 4.2 - Схема к определению гидравлически гладких и гидравлически шероховатых труб.

Для гидравлически шероховатых труб выступы шероховатости не покрыты ламинарным подслоем, они “вклиниваются” в турбулентное ядро потока, увеличивая беспорядочность движения. Шероховатость при этом существенно влияет на величину потерь давления.

Толщина ламинарного подслоя определяется из условия, что число Рейнольдса,

определяемое по средней скорости в этом слое, меньше или равно критическому:

Re 2300 .

Из этого соотношения следует, что, чем больше средняя скорость движения жидкости в трубопроводе, тем больше средняя скорость в ламинарном слое υ и тем меньше при этом будет толщина слоя.

При увеличении скорости движения толщина ламинарного слоя уменьшается и,

наоборот, при уменьшении скорости движения толщина ламинарного слоя увеличивается. Одна и та же труба в зависимости от скорости движения может быть и гидравлически гладкой, и гидравлически шероховатой.

При нагревании жидкости, когда вязкость и, соответственно, толщина ламинарного слоя уменьшаются, гидравлически гладкая труба также становится гидравлически шероховатой.

Отметим, что при ламинарном режиме все трубы являются гидравлически гладкими, так как ламинарный режим имеет место по всему сечению трубы.

35

Экспериментальные данные Г.А. Мурина на промышленных трубах представлены на рисунке 4.3.

Рисунок 4.3 - Экспериментальные данные Г. А. Мурина.

Из рассмотрения графика можно сделать следующие выводы.

1. В области ламинарного режима в логарифмических координатах, все опытные точки, отвечающие различным шероховатостям, практически совпадают с прямой линией

1-2, построенной по формуле:

Следовательно, здесь зависит только от числа Re и не зависит от шероховатости.

2. В области турбулентного режима (Re>2300) имеется целое семейство кривых,

расположенных правее прямой линии 3-4. Здесь коэффициент гидравлического трения зависит от двух параметров - числа Re и относительной шероховатости. Результаты экспериментов удовлетворительно описываются универсальной формулой Альтшуля:

3. В области турбулентного режима при небольших значениях Re опытные точки практически совпадают с прямой 3-4, построенной по формуле Блазиуса:

Это зона гидравлически гладких труб, где коэффициент трения не зависит от шероховатости, так как она покрыта ламинарным подслоем. Отметим, что чем больше шероховатость, тем при меньших Re (больших значениях толщины ламинарного слоя)

исчезает зависимость от шероховатости.

4. При увеличении скорости движения (числа Re) опытные точки начинают отклоняться от прямой линии 3-4 и укладываются на семейство кривых между линиями

3-4 и А-B. Физически это означает, что бугорки шероховатости выступают в турбулентное ядро потока и относительная шероховатость оказывает практически такое же влияние на

36

коэффициент трения, как и число Re. Это зона гидравлически шероховатых труб, где

коэффициент трения определяется по формуле (4.5):

0,11 ( 68Re dэ )0,25

5.При больших значениях числа Re коэффициент трения перестает зависеть от

Re, опытные точки располагаются на прямых, параллельных оси Re и подчиняются формуле Шифринсона:

Физически это означает, что при больших скоростях движения толщина ламинарного слоя очень мала, все бугорки шероховатости находятся в турбулентном ядре,

являются источниками образования вихрей и полностью определяют величину сопротивления трубопровода.

Это зона абсолютно шероховатых труб. Вследствие того, что здесь

коэффициент трения не зависит от числа Re (скорости движения), в формуле Дарси-

Вейсбаха (4.3) потери давления пропорциональны квадрату скорости.

Зону абсолютно шероховатых труб часто называют зоной квадратичных сопротивлений, а зону шероховатых труб - доквадратичной.

При выполнении практических расчетов коэффициент гидравлического трения в области турбулентного режима во всех случаях можно определять по формуле Альтшуля

(4.5). Слагаемое (68/Re или э/d), которое в данной ситуации незначительно влияет на коэффициент трения, дает и незначительный вклад в его величину.

4.2. Определение экспериментального значения коэффициента трения

Из уравнения (4.1) потери давления p1-2 равны:

В случае отсутствия местных сопротивлений между сечениями 1-1 и 2-2 потери давления равны потерям по длине потока:

37

Следовательно, измерив разность давлений между сечениями, расход жидкости

(для определения скоростей) и зная геометрию трубопровода, можно вычислить экспериментальное значение потерь по длине, а из формулы (4.9) - коэффициент гидравлического трения э.

В частном случае, для горизонтального трубопровода постоянного диаметра

(z1=z2, υ1=υ2) и при отсутствии местных сопротивлений вместо уравнения (4.9) получим:

Входящая в формулу (4.11) разница давлений может быть определена с помощью приборов для измерения давления: пьезометров, манометров или дифференциального манометра.

Внимание!

Формула (4.11) справедлива для частного случая движения жидкости в

горизонтальном трубопроводе постоянного диаметра.

4.3Проведение лабораторной работы

Цель:

1.Экспериментальная иллюстрация формулы, определяющей связь потерь механической энергии потока жидкости по длине трубы с параметрами трубы и сечения.

2.Определение теоретического и экспериментального значения коэффициента трения

.

3.Построение графиков зависимости Т (Re), э (Re).

Работа выполняется на модуле М1 «Потери напора по длине» (приложение А).

Для выполнения работы необходимо:

1.Включить насос Н1 на панели управления (смотри рисунок 1.1);

2.Установить необходимый расход с помощью вентилей В2, В1 и выходного вентиля В4 (смотри рисунок 1.2);

3.Снять показания по ротаметрам Р1 и Р2 (смотри рисунок 1.1) и внести данные в таблицу 4.1;

38

4.Снять показания пьезометров (смотри рисунок 1.1) и внести данные в таблицу 4.1.

5.После достижения установившегося режима изменить расход с помощью вентиля В4 (смотри рисунок 1.2) повторить все измерения.

6.Для надежной серии опытов рекомендуется произвести измерения для трех расходов.

Обработка опытных данных:

1)По результатам измерений вычисляются следующие величины:

1.Перейти от показаний ротаметров к расходу (смотри градуировочную характеристику ротаметров приложение Б)

2.Потери напора по длине:

hg h1 h2 ;

3.Средняя скорость потока в трубе:

4 Q ;

d 2

Геометрические характеристики модуля (d, L) представлены в приложении А.

4. Экспериментальный гидравлический коэффициент трения по формуле:

5. Число Рейнольдса:

Re d ,

Жидкость вода: воды = 1000 кг/м3; коэффициент динамической вязкости воды =1.10-3 Па.с.

6. Теоретический гидравлический коэффициент трения (смотри формулы 4.4 - 4.7).

2)Результаты измерений внести в таблицу 4.1. Результаты полученных вычислений внести в таблицу 4.2.

Таблица 4.1 – Результаты измерений. Лабораторная работа № 3.

Таблица 4.2 – Результаты вычислений. Лабораторная работа № 3.

№ режима Расход, м/с Потери Скорость, υ, э Число Re Т напора, hg, м м/с

39