84. Расчет тр/проводов, трансп-их неньютон-е жид-ти.

Рассмотрим трубопровод со стационарным движением по нему неньютоновской жидкости имеющей неразрушен­ную структуру в форме цилиндрического ядра, состоящего, на­пример, из парафинистой нефти. Первый член уравнения Шведова–Бингама характеризует движение неньютоновской жидкости, а второй член – минимальное предель­ное напряжение сдвига, превышение которого вызывает начало движению неньютоновской жидкости; μ*– кажущаяся (эффективная) вязкость неньютоновской жидкости, т. е. вязкость, зависящая от градиента скорости dv/dr. Совместное движение неньютоновской жидкости и ядра воз­можно при условии τ > τ₀, т. е. в том случае, если касательное напряжение τ всегда будет больше минимального предельного напряжения сдвига т₀. Уравнение равновесия сил давления и сил трения для произ­вольной части потока имеет вид πr²Δp=2πτℓτ,откуда τ =rΔp/(2ℓ). Подставим в ур-е Ш-Б. и получим: rΔp/(2ℓ)=-μ* dv/dr+ τ₀ (1.1). (1.2). Интегрируя последнее, получим выражение для скорости ньютоновской жидкости в след. виде: (1.3). Постоянную интегрирования находим уз условия, что r=R, v=0, т.е. (1.4). Подставим последнее в (1.3) получим: (1.5).

Данное ур-е справедливо для кольцевого пространства жид-ти, заключенной м/у стенкой трубы и цилиндрич. ядром, т.е. r₀≤r≤R₀. Скорость движ-я ядра найдем из выр-я (1.5), подставляя в него вместо r→r₀, а вместо v→v₀: (1.6). Суммарный расход неньютон. жид-ти по трубе опр-тся из расхода ядра Q₀ и расхода ламинарного слоя Q_л. Расход ядра потока .

Расход ламинар. кольца потока жид-ти опр-тся из выражения:

Суммарный расход составит: (1.7).

Подставляя данное ур-е выражения (1.6) и (1.5) и интегрируя, получим:

(1.8).Подставляя в полс. ур-е вместо r₀ выр-е и вместоперепад давления, при котором данная неньютоновская ж-ть начинает «страгиваться», получим окончательно:

(1.9).

Представим в посл. уравнении отношение в след. виде:

(1.10)

и после подстановки его в выр-е (1.9) получим след. формулу: 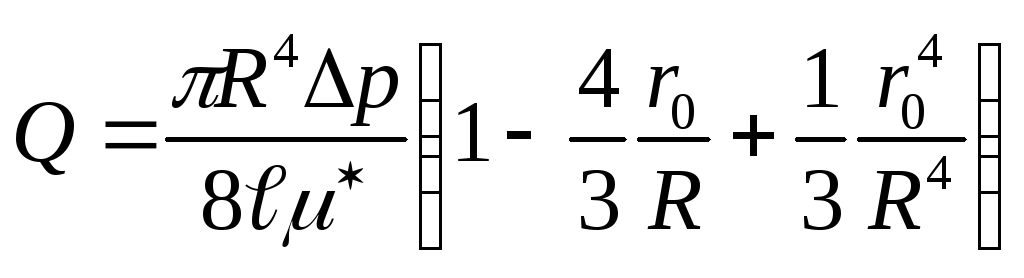(1.11).

Средняя скорость потока неньютон. жид-ти опр-ся так:

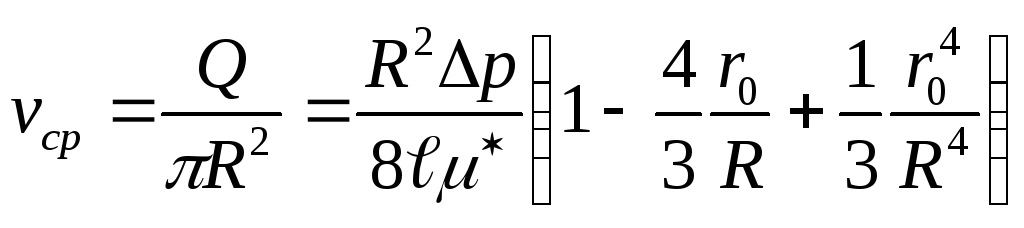(1.12). Заменяя в (1.11) r₀/R на , получим:(1.13).

Вместо подставими решим последнее ур-е отн-но, получим:(1.14).

Заменяя в (1.14) R на D/2 , расход жид-ти Q на среднюю скорость потока , получим:(1.15).

В последнем ур-ии первый член характеризует потери напора при ламинарном режиме движ-я ньютоновской жид-ти, а второй – увел-е гидравлических потерь за счет пластических свойств неньютон. жид-ти. При =0, выр-е (1.15) принимает вид формулы Пуайзеля:.

85.Основная расчетная формула газопровода высокого давления. Три основные расчетные задачи простого газопровода.

Три основные расчетные задачи простого газопровода:

1. Qат ; D Найти P

2. P ; D Найти Qат

3. Qат ; P Найти D

- для несжимаемой жидкости

; ;;;

; ;

;

;

основная формула

где: λ – коэффициент гидродинамических сопротивлений;

К – шероховатость поверхности труб.

Определение среднего давления в газопроводе.

Рассмотрим газопровод длинной L, диаметром D с начальным давлением Pн и конечным Pк. Требуется определить давление в любой точке, например М, на расстоянии x от начала газопровода. Уравнение расхода для участка АМ запишется так:

;

А для участка МВ

Учитывая постоянство расхода по длине газопровода, приравняем правые части этих уравнений, тогда:

.

Кривая, описываемая этим уравнением, является параболой. Из характера этой кривой видно, что при длинне газопровода градиент давления постоянно увеличивается, что свидетельствует о непостоянстве гидравлического уклона. В начале газопровода, когда давление и плотность газа высокие, удельный объём газа мал и скорость незначительная, потери давления в газопроводе небольшие, т.е градиенты давления малы. По мере удаления от начала трубопровода давление падает, а удельный объём газа увеличивается, что приводит к увеличению скорости движения газа и, соответственно, к росту потерь давления на трение, пропорциональных квадрату скорости.

Примем , тогда

, тогда

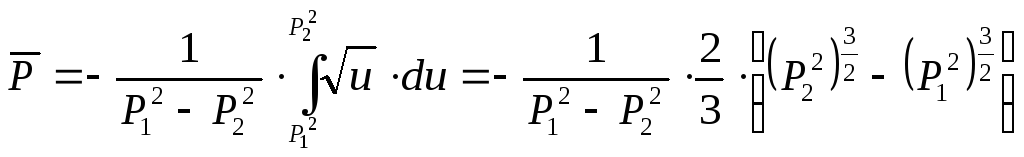
После преобразования:

.