82.Гидравлический расчет простого напорного трубопровода при изотермическом режиме течения жидкости.
Принимаем,
что движется однофазная ж-ть. Гидравлич.
Расчет сводится к определению: диаметра,
нач.давления Р1,
пропускной способности Q.
В основе гидравлических расчетов лежит
уравнение Бернулли.
Каждый
член ур-я имеет размерность высоты: z1
– положение линии тока над плоскостью
сравнения;
- пьезометрическая (статическая) высота;
- динамическая высота (скоростной напор).
Эти напоры расходуются на преодоление сил трения - hтр, и местных сопротивлений - hмс в трубопроводах (задвижки, отводы)
Потери напора на трение.
Для трубопровода круглого сечения ф-ла Дарси-Вейсбаха:
;
hтр – потери напора на преодоление сил трения; λ – коэф.гидравлич. сопротивления; l – длина труб, м; D – диаметр труб, м; ρ – плотность ж-ти, кг/м3; υ – средняя скорость течения ж-ти, м/с; Q – расход ж-ти, м3/с; g – ускорение свободного падения, м/с2;γ – функция Рейнольдса, Δ (γ=f(Re,Δ)) ;Δ – абс.шероховатость трубы, мм.
Если
течение ламинарное (Re<2300),
то λ=64/Re;
;
;
Q
– расход ж-ти, м3/с;
- площадь сечения трубы, м2;
ν – кинематическая вязкость ж-ти, м2/с,
сСт; D
– внутр диам, м; μ – дин вязкость ж-ти,
Па·с.
При
турбулентном течении ж-ти (Re>2300)
для определения λ применяют несколько
экспериментальных формул:1.Для переходного
периода от ламинарного к турбулентному;
2.Для смешанного режима; 3.Для квадратичного.
Однако без ущерба для точности в интервале
Re
от 2300 до 105
λ можно определить по формуле Блаузиуса:
,
и для квадратичного режима λ опр-ся по
формуле Шифринсона:
Потери напора на местные соротивления.
Местные
сопротивления возникают: в закруглениях
труб; на резких поворотах; в отводах,
задвижках, кранах и т.д. Местные
сопротивления необходимо учитывать
при расчете всасывающих линий насосов
и компрессоров. При больших длинах
напорных трубопроводов, уд. вес местных
сопротивлений невелик и им пренебрегают.
υ
– ср.скорость движ.ж-ти за местным
сопротивлением; ξ – коэф.местного сопр.,
кот. зависит от формы МС,от Re
и шероховатости, а для запорных устройств
и от степени их открытия. Удобно определять
местные сопротивления по эквивалентной
длине. Экв. длина (lэ)
– длина прямого уч-ка трубопровода
данного d,
из усл-я, если hтр=hмс.
lэ
можно найти по ф-ле Дарси-Вейсбаха
;
В
“рельефных” (не гориз-х) труб-х перепад
давл считают след обр:
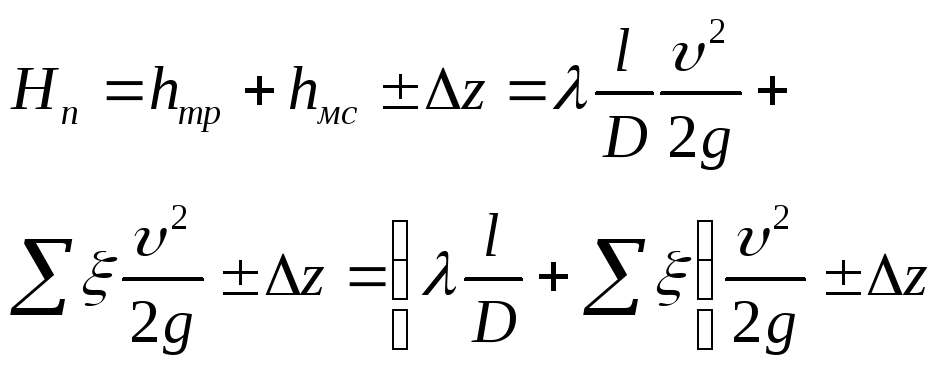;Δz=zн-zк
Короткие трубо-ды (всасывающие линии насосов) рассчитываются также по этой ф-ле (вместо Δz – разность уровня вала насоса и ж-ти в резервуаре).
83.Гидравлический расчет сложного напорного трубопровода при изотермическом режиме течения жидкости.
Принимаем,
что движется однофазная ж-ть. Гидравлич.
Расчет сводится к определению: диаметра,
нач.давления Р1,
пропускной способности Q.
В основе гидравлических расчетов лежит
уравнение Бернулли.
Каждый
член ур-я имеет размерность высоты: z1
– положение линии тока над плоскостью
сравнения;
- пьезометрическая (статическая) высота;
- динамическая высота (скоростной напор).
Эти напоры расходуются на преодоление сил трения - hтр, и местных сопротивлений - hмс в трубопроводах (задвижки, отводы)
Потери напора на трение.
Для трубопровода круглого сечения ф-ла Дарси-Вейсбаха:
;
hтр
– потери напора на преодоление сил
трения; λ – коэф.гидравлич. сопротивления;
l
– длина труб, м; D
– диаметр труб, м; ρ – плотность ж-ти,
кг/м3;
υ – средняя скорость течения ж-ти, м/с;
Q
– расход ж-ти, м3/с;
g
– ускорение свободного падения, м/с2;γ
– функция Рейнольдса, Δ (γ=f(Re,Δ))
;Δ – абс.шероховатость трубы, мм. Если
течение ламинарное (Re<2300),
то λ=64/Re;
;
;
Q
– расход ж-ти, м3/с;
- площадь сечения трубы, м2;
ν – кинематическая вязкость ж-ти, м2/с,
сСт; D
– внутр диам, м; μ – дин вязкость ж-ти,
Па·с.
При
турбулентном течении ж-ти (Re>2300)
для определения λ применяют несколько
экспериментальных формул:1.Для переходного
периода от ламинарного к турбулентному;
2.Для смешанного режима; 3.Для квадратичного.
Однако без ущерба для точности в интервале
Re
от 2300 до 105
λ можно определить по формуле Блаузиуса:
,
и для квадратичного режима λ опр-ся по
формуле Шифринсона:
Потери напора на местные соротивления.
Местные
сопротивления возникают: в закруглениях
труб; на резких поворотах; в отводах,
задвижках, кранах и т.д. Местные
сопротивления необходимо учитывать
при расчете всасывающих линий насосов
и компрессоров. При больших длинах
напорных трубопроводов, уд. вес местных
сопротивлений невелик и им пренебрегают.
υ
– ср.скорость движ.ж-ти за местным
сопротивлением; ξ – коэф.местного сопр.,
кот. зависит от формы МС,от Re
и шероховатости, а для запорных устройств
и от степени их открытия. Удобно определять
местные сопротивления по эквивалентной
длине. Экв. длина (lэ)
– длина прямого уч-ка трубопровода
данного d,
из усл-я, если hтр=hмс.
lэ
можно найти по ф-ле Дарси-Вейсбаха
;
В
“рельефных” (не гориз-х) труб-х перепад
давл считают след обр:
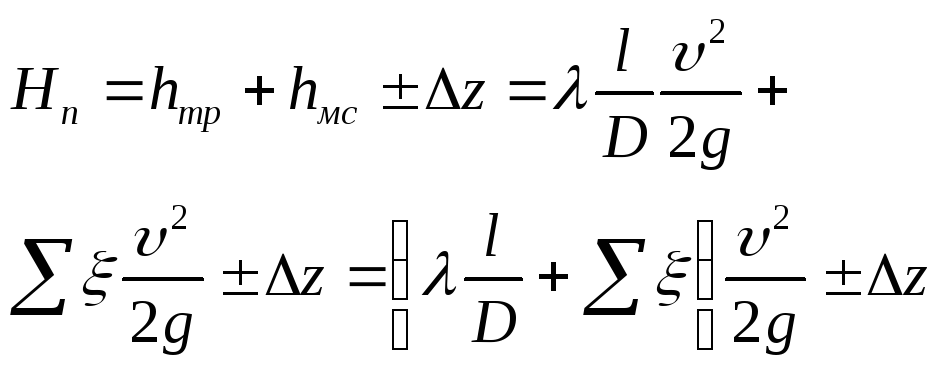;Δz=zн-zк
Короткие трубо-ды (всасывающие линии насосов) рассчитываются также по этой ф-ле (вместо Δz – разность уровня вала насоса и ж-ти в резервуаре).
Пример.
Газопровод с параллельными нитками
В отд. случаях д/увеличения надежности работы газосборной сети прокладывают 2 или несколько параллельных ниток.
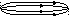
Рис.1. Расчетная схема газопровода с параллельными нитками
Рассмотрим серию газопроводов, проложенных параллельно, имеющих одинаковую длину и работающих с одинаковыми начальными и конечными давлениями.
Для каждого из газопроводов можно записать:
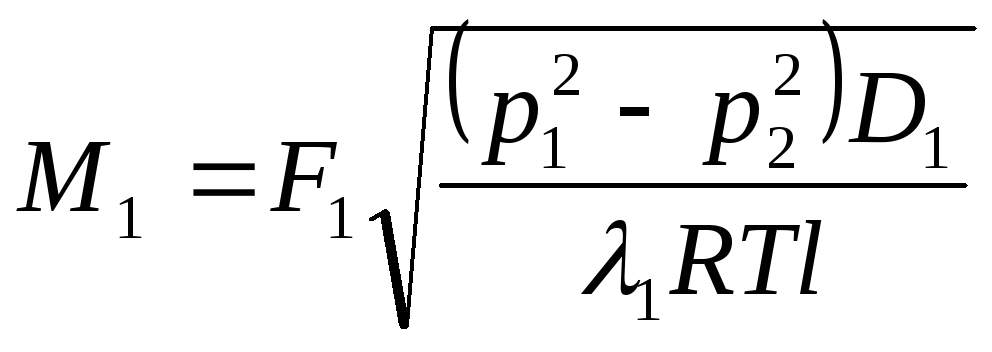
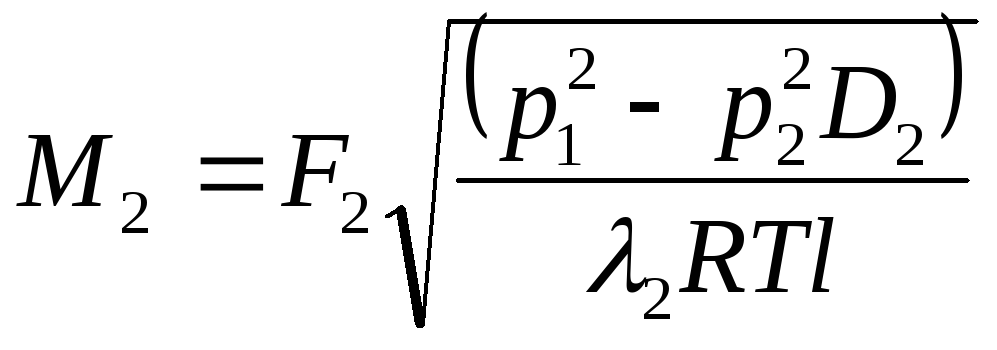
Тогда
пропускная способность всей серии
газопроводов
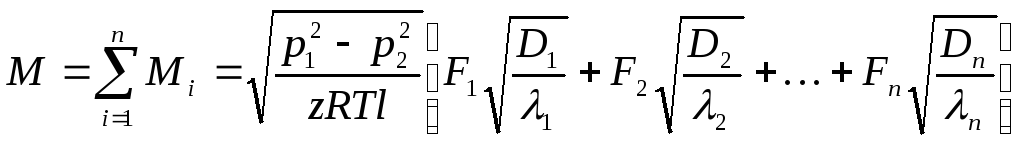
В
частном случае, часто встречающемся на
практике, диаметры параллельных ниток
одинаковы, тогда
где n-число парал. ниток.
Используя
понятие эквивалентного диаметра
газопровода, т.е. диаметры, имеющего
такую же пропускную способность, имеем
Окончательно
получим
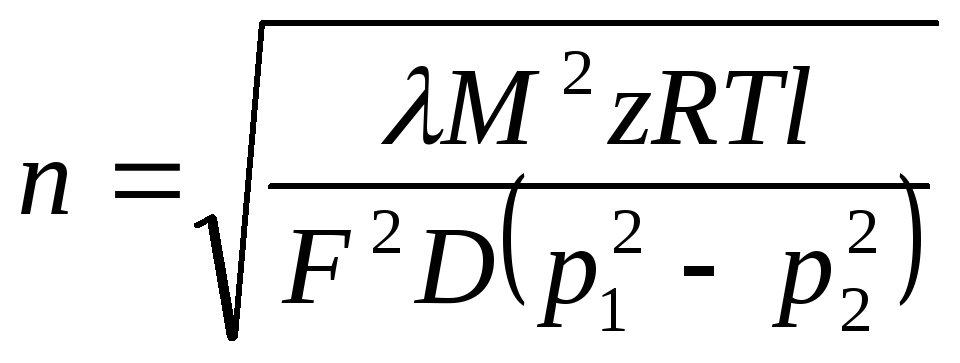
Задача решается таким же образом относительно диаметра каждй из ниток, если задано их число.