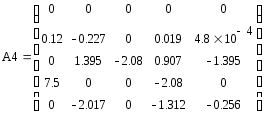
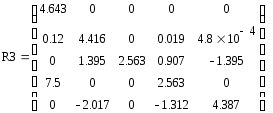
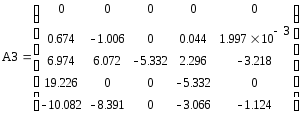
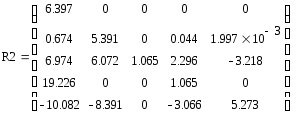
Итерация 1:

Итерация 2:

Итерация 3:

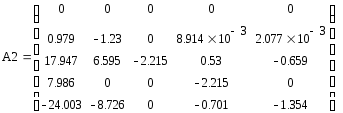
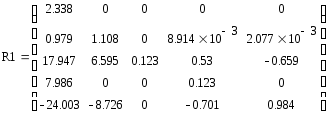
Итерация 4:

Итерация 5:

Поскольку элементы матрицы R_0 равны нулю, вычисления были выполнены верно.

Характеристический полином системной матрицы А:

Тогда передаточная матрица равна:

Рассчитаем матричную передаточную функцию:

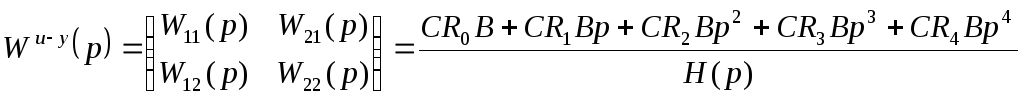
В результате были получены следующие канальные функции:

Для сравнения представлены ПФ, найденные в пункте 2.2 раздела 2 данной курсовой работы:

Итак, полученные разными путями ПФ практически (до третьего знака после запятой) совпадают.

5.4 Исследование и преобразование матрично-векторных ММ УОУ

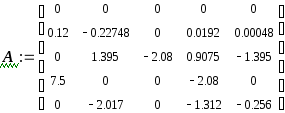
Системная матрица А:

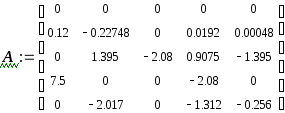
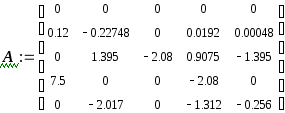
Матрица управления В:

Матрица наблюдений С:

5.5 Исследование фундаментальных свойств уоу по его матрично-векторной мм

В данном пункте приводится оценка управляемости и наблюдаемости. Эти свойства исследуются как по отдельным входам и выходам, так и в целом для объекта (файлы с расчётами OcenkaUpr.mcd и OcenkaNabl.mcd прилагается).

5.5.1 Исследование управляемости УОУ и его каналов воздействия на выходные переменные

Управляемость – свойство динамической системы, при которой её можно перевести из любого начального состояния x₀ в любое конечное за конечный промежуток времени.

Для построения и оценки матриц управляемости и наблюдаемости используется пакет MathCAD.

Свойство управляемости оценивается матрицей управляемости:

.

Динамическая система является вполне управляемой, если ранг матрицы равен. Система не вполне управляема, если ранг матрицыменьшеи больше 0. Система является полностью неуправляемой, если ранг матрицы управляемостиравен нулю.

Формула для нахождения матрицы управляемости:

,

где A – системная матрица, B – входная матрица, С – матрица наблюдения.

n=5 – порядок системы.

Оценка управляемости уоу по входу u1:

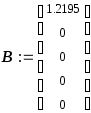
Вывод: система вполне управляема по входу u₁, т. к. ранг матрицы равен порядку системы, т.е. равен 5.

Оценка управляемости уоу по входу u2:

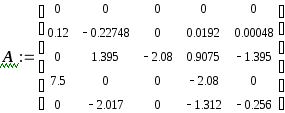
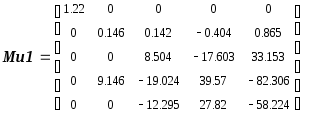
Вывод: система не вполне управляема по входу u₂, т. к. ранг матрицы равен 3, т.е. меньше порядка системы и больше 0.

Дефект d = n – r(Mu) = 5 – 3 = 2.

Оценка управляемости системы в целом:

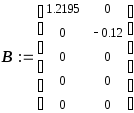
Вывод: в целом система вполне управляема, т. к. ранг матрицы равен порядку системы, т.е. равен 5.

5.5.2 Исследование наблюдаемости УОУ и его каналов измерения выходных переменных

Динамическая система считается наблюдаемой, если путём наблюдений выходной переменной y система за сколь угодно малый промежуток времени t от t₀ до t₁, где t₁>t₀ наблюдается вектор входных механизмов u и, зная математическую модель динамической системы, можно восстановить истинное состояние вектора состояния в момент t₀.

Для оценки наблюдаемости динамической системы существует критерий наблюдаемости:

Система является вполне наблюдаемой, если ранг матрицы наблюдаемости равен порядку этой системы. Система является частично наблюдаемой, если ранг матрицы наблюдаемости меньше и больше нуля. Система является полностью ненаблюдаемой, если ранг матрицы наблюдаемости равен нулю.