4.4. Сравнительная оценка синтезированных сау

В результате применения операторного метода и метода отождествления высших производных при синтезе закона управления объектом были получены САУ, удовлетворяющие в обоих случаях критериальной стратегии.

Однако, несмотря на данное преимущество каждый из этих методов имеет свои существенные недостатки:

1. Операторный метод синтеза ЗУ приводит к получению трудно реализуемого управляющего устройства высокого порядка.

2. Метод отождествления высших производных приводит к формированию АСУ с ЗУ, содержащим производные высших порядков, вплоть до (n-1)-й, что делает закон практически нереализуемым.

5 Построение и исследование матрично-векторных форм математических моделей (мм) уоу и выработка ксс синтеза зу состоянием уоу в одномерном и многомерном варианте

5.1 Построение матрично-векторной формы (МВ) ММ УОУ

Для построения МВ-формы ММ неполных и многомерных УОУ используется прямой способ построения МВ ММ по структурной схеме УОУ. Если считать, что исследуемая в работе схема соответствует реальной физической или технической структуре объекта, МВ-форму легко получить, приняв за переменные состояния (ПС) выходные переменные всех входящих в схему динамических звеньев. Также для удобства построения матрично-векторной ММ УОУ введем условные промежуточные переменные.

На рисунке 5.1 представлена структурная схема УОУ с указанием на ней переменных состояния, промежуточных переменных, входных и выходных переменных, передаточных функций звеньев.

Рисунок 5.1 - Схема УОУ с обозначением переменных состояния

Поскольку все ДЗ схемы имеют первый порядок, то последовательная запись их ДУ в систему в форме Коши, в которой входной сигнал звена представлен с учетом полной структуры его формирования из ПС и входных воздействий, позволяет получить МВ форму ММ.

Для составления дифференциальных уравнений (ДУ) воспользуемся следующими преобразованиями:

Для , получим:.

Для , получим:.

Для , получим:, где k₀=b₁; k₁=b₀–a₀k₀.

В результате система ДУ будет иметь следующий вид:

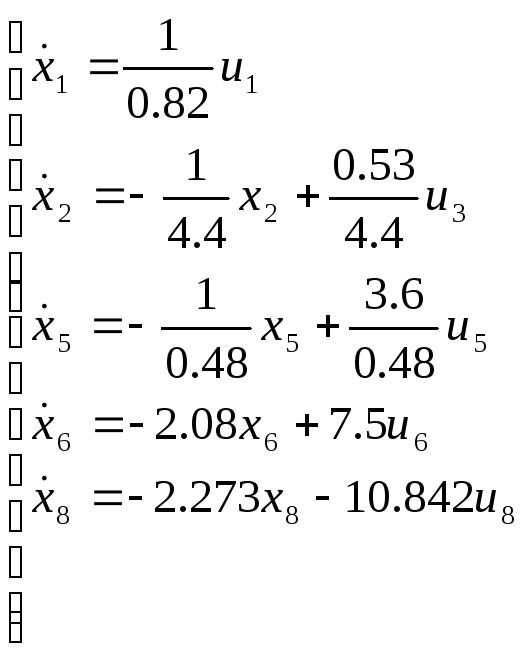
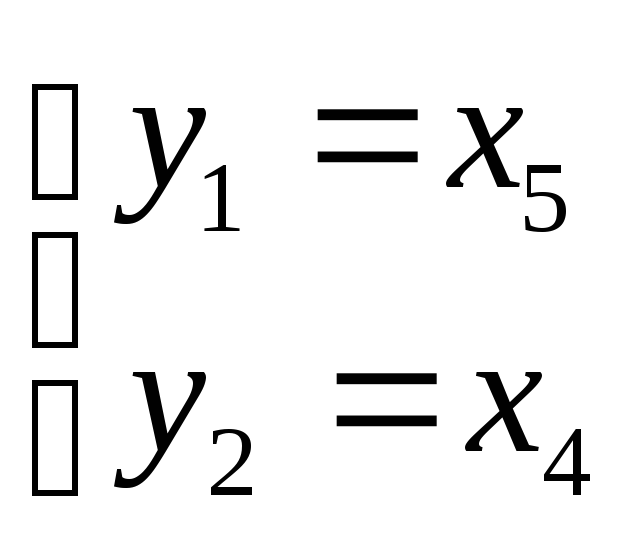
Вычислим коэффициенты k_i:

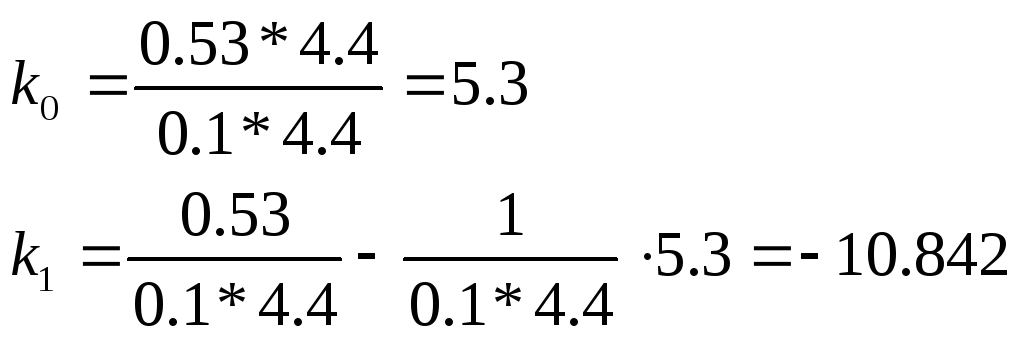
Выведем значения переменных, введённых для упрощения преобразований:

Таким образом, значения временных переменных равны:

Подставим эти значения в ДУ:

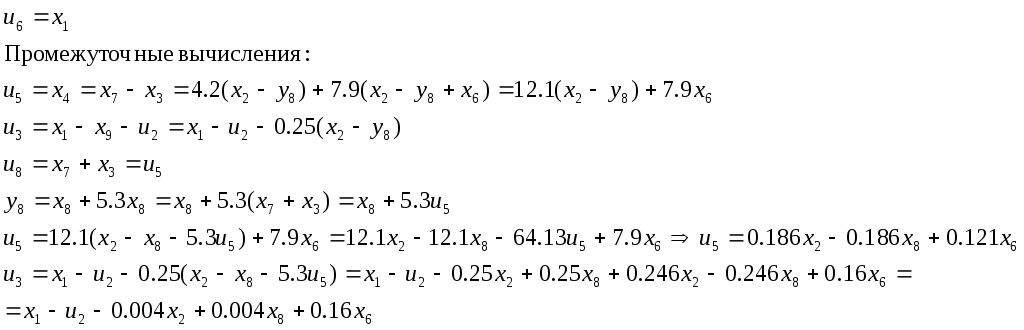Применив элементарные преобразования, получим:

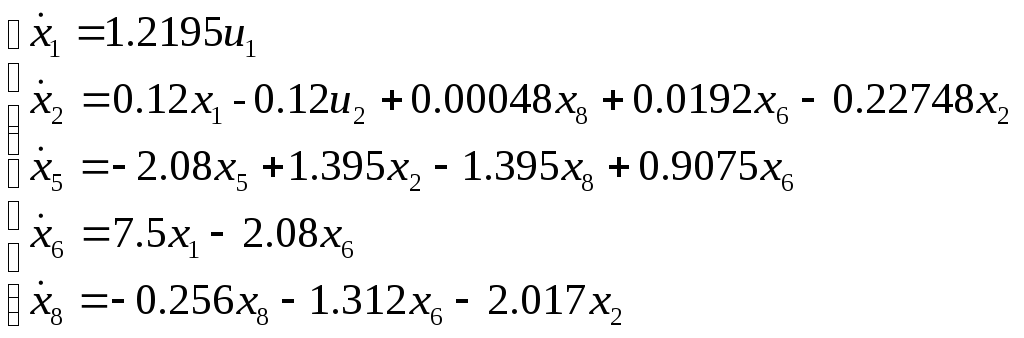
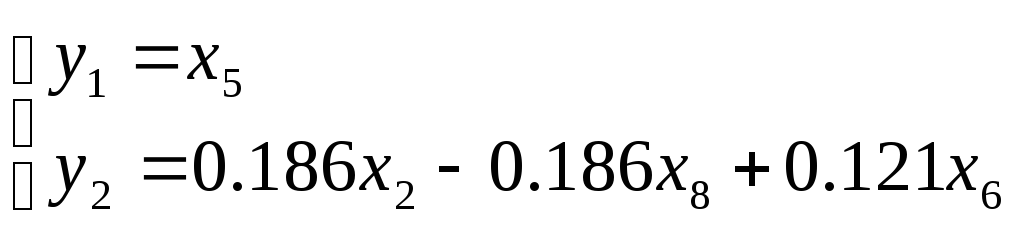
5.2 Проверка эквивалентности вход-выходной и матрично-векторной ММ

По системе ДУ, образующих МВ модель, построим структурную схему объекта (рисунок 5.2) и исследуем его в системе Classic (файл 5.MDL прилагается).

В основе построения структурной схемы по МВ описанию лежат правила:

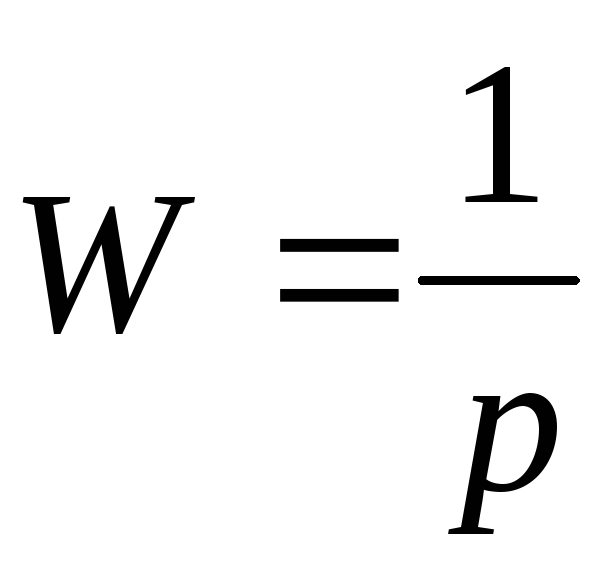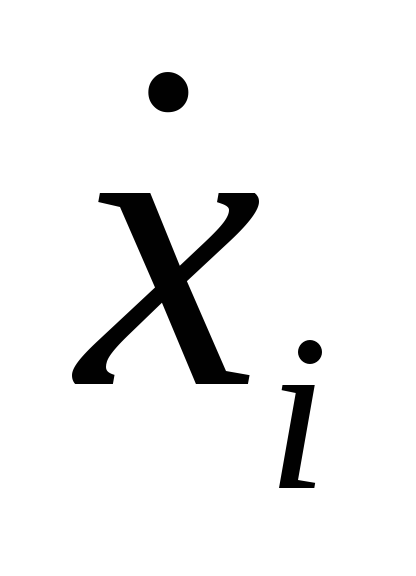• для каждого ДУ в схему добавляется интегратор (звено с ), входным сигналом которого является производная переменной состояния (), а выходным – сама переменная состояния;

• в соответствии с ДУ на вход интегратора через усилительные звенья подаются входные воздействия и переменные состояния;

• выходные сигналы формируются по уравнению наблюдения как сумма переменных состояния.

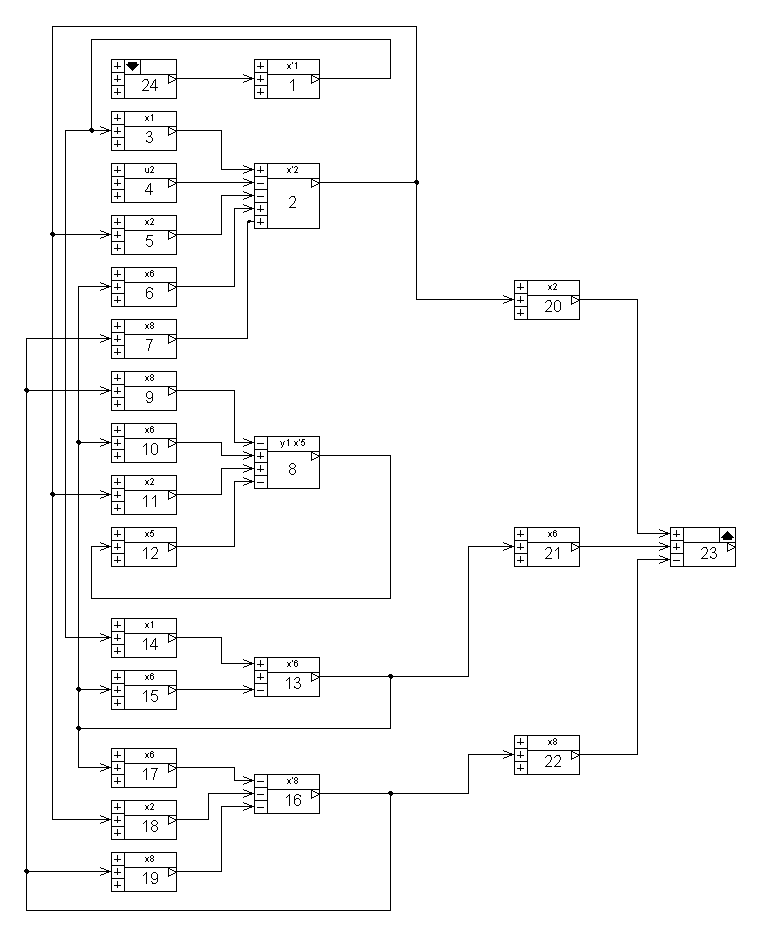
Рисунок 5.2 - Модель ДУ в пакете Classic

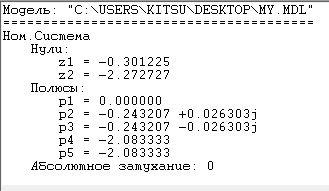
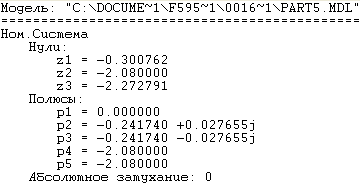
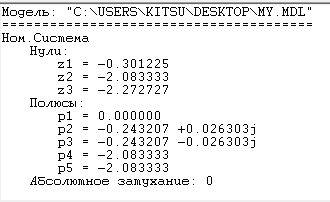
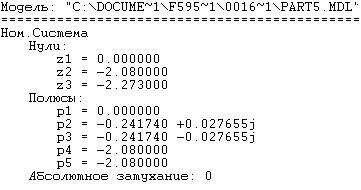
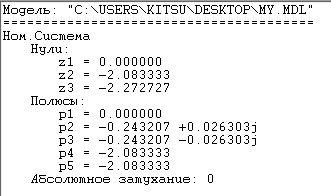
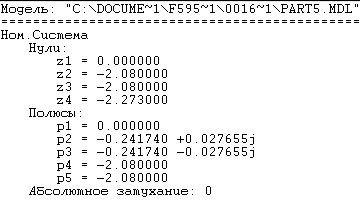
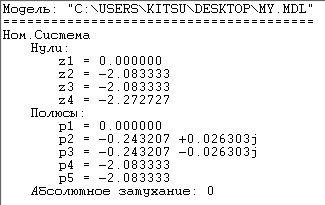
Для проверки идентичности схемы вход-выходной ММ и схемы МВ ММ найдем нули и полюса УОУ (таблица 5.1).

Таблица 5.1 – Нули и полюсы УОУ

Схема моделирования МВ формы ММ	Схема моделирования вход-выходной ММ
U1-Y1
U1-Y2
U2-Y1

Продолжение таблицы 5.1

U2-Y2

Значения нулей, полученные по матрично-векторной ММ и вход-выходной ММ, практически совпадают. Следовательно, преобразования были выполнены корректно.

5.3 Построение передаточной матрицы УОУ по МВ ММ

Запишем модель объекта в матрично-векторной форме. Вычислим далее передаточную матричную функцию многомерной системы с помощью алгоритма Леверье – Фадеева.

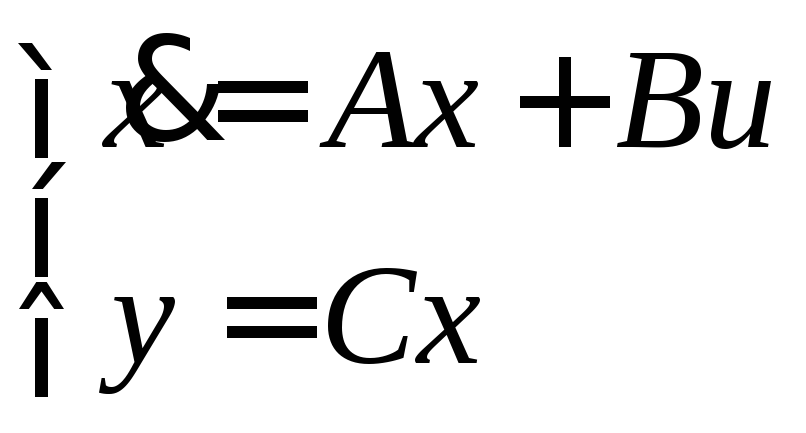
где

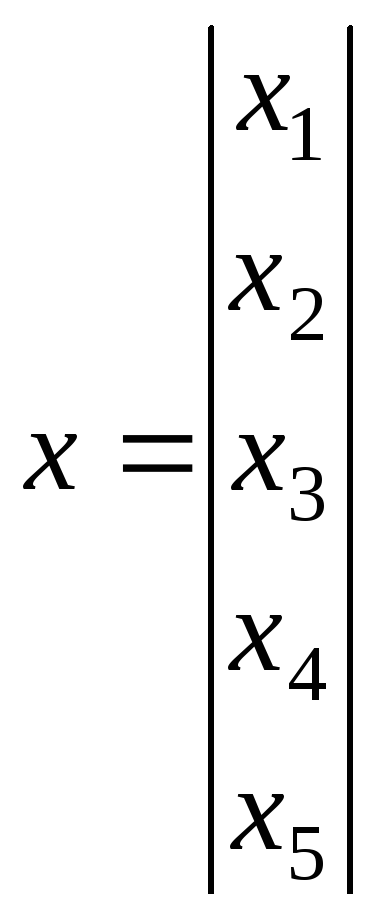- вектор переменных состояния,

- вектор входных значений

- вектор выходных воздействий

Системная матрица А:

Матрица управления В:

Матрица наблюдений С:

Матрицу , задающую связь между векторами выходаи входаназывают передаточной матричной функцией многомерной системы. Её построение проще осуществляется с использованием алгоритма Леверье – Фадеева, который состоит в следующем:

представим передаточную матричную функцию как отношение двух полиномов:

где

–характеристический полином

–некоторый матричный полином

Коэффициенты и матрицыможно вычислить по следующим формулам:

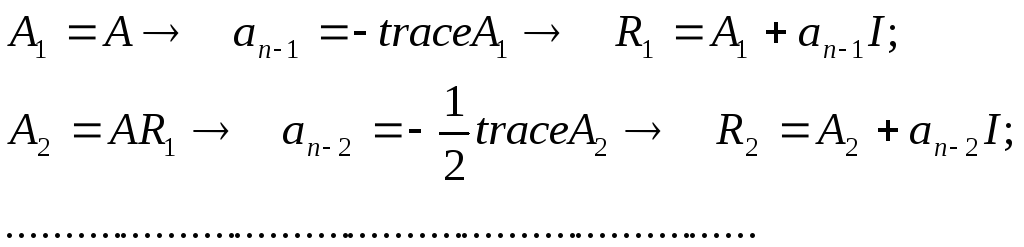
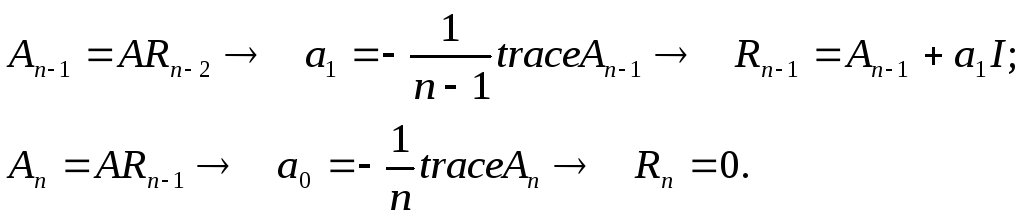
Окончательно

Этот алгоритм для УОУ данного варианта реализуем с помощью Mathcad 14 (файл 5 часть, п. 5.mсd прилагается):