
- •Введение
- •1. Сущность сейсморазведки
- •2. История возникновения сейсморазведки
- •Часть 1. Физические и геологические основы сейсморазведки
- •1. Упругие волны в безграничной среде
- •1.1 Основы теории упругих волн
- •1.2 Продольные и поперечные волны
- •1.4. Принципы геометрической сейсмики
- •1.5. Поверхностные волны
- •1.6. Распространение сейсмических волн
- •2. Отражение и преломление на границе раздела двух сред
- •2.1. Образование вторичных волн
- •2.2. Законы отражения
- •2.3. Закон преломления
- •2.4. Образование головных (преломленных) волн
- •3. Волны в многослойных средах
- •3.1. Кратные волны
- •3.2. Преломленные и отраженные волны в слоистых средах
- •4. Криволинейные границы
- •4.1. Отраженные волны от криволинейных границ
- •4.2. Дифракция волны
- •4.3. Особенности отраженных волн от шероховатых границ
- •4.4. Рефрагированные волны
- •4.5.Структура волнового поля
1.4. Принципы геометрической сейсмики
Процесс распространения сейсмических волн в упругих средах подчиняется ряду важных для теории и практики принципам (постулатам).
Согласно принципу Ферма, время движения волны по лучу минимально. На основе этого принципа сравнительно просто определить форму сейсмических лучей. В однородной изотропной среде, где V=const сейсмические лучи представлены прямыми линиями. В неоднородных изотропных средах V=grad, т.е. в средах, упругие константы которых зависят от координат пространства, форма сейсмического луча существенно усложняется, поскольку они становятся криволинейными. Поиск траектории таких лучей осуществляется на основе принципа Ферма и математически сводится к решению вариационной задачи на определение минимума времени пробега волны между двумя точками А и В:
t
=
 ,
(1.17)
,
(1.17)
где ds – элемент длины дуги, соединяющей точки А и В.
В соответствии с
принципом
Гюйгенса –
любая точка,
взятая на поверхности изохроны,
соответствующей фронту волны, является
элементарным источником колебаний.
Принцип
Гюйгенса
в простейшей форме можно использовать
для определения положения фронтов волн
для разных моментов времени. Пусть фронт
волны в некоторый момент времени t=t![]() представлен
линией 1
(рис.1.9). Согласно этому принципу, форма
фронта волны 2
в момент времени t
представлен
линией 1
(рис.1.9). Согласно этому принципу, форма
фронта волны 2
в момент времени t![]() =
t
=
t![]() +∆t
будет
представлять собой огибающую к
элементарным фронтам волн радиуса
∆r=∆t
+∆t
будет
представлять собой огибающую к
элементарным фронтам волн радиуса
∆r=∆t![]() .
.
Р ис.1.9.
Схема построения фронта волны:1-
положение исходной изохронны на 1
момент
времени t
ис.1.9.
Схема построения фронта волны:1-
положение исходной изохронны на 1
момент
времени t![]() ;
2 – положение
фронта волны в момент времени t
;
2 – положение
фронта волны в момент времени t![]()
На этом принципе основана группа способов решения прямых и обратных задач сейсморазведки, условно называемая методом полей времен, который широко применяется для интерпретации волновых полей.
Френель на основе принципа Гюйгенса первым сформулировал количественный подход к оценке размеров части среды, активно участвующей в передаче волны от источника к точке наблюдения. Если задать плоскость и построить линию перпендикулярную к ней и соединяющую источник О и точку приема М, то на этой плоскости можно построить зоны Френеля (рис. 1.10) – систему концентрических колец такой ширины, чтобы при переходе от внутреннего контура к внешнему, время прихода колебаний в точку М изменялось бы на половину периода.
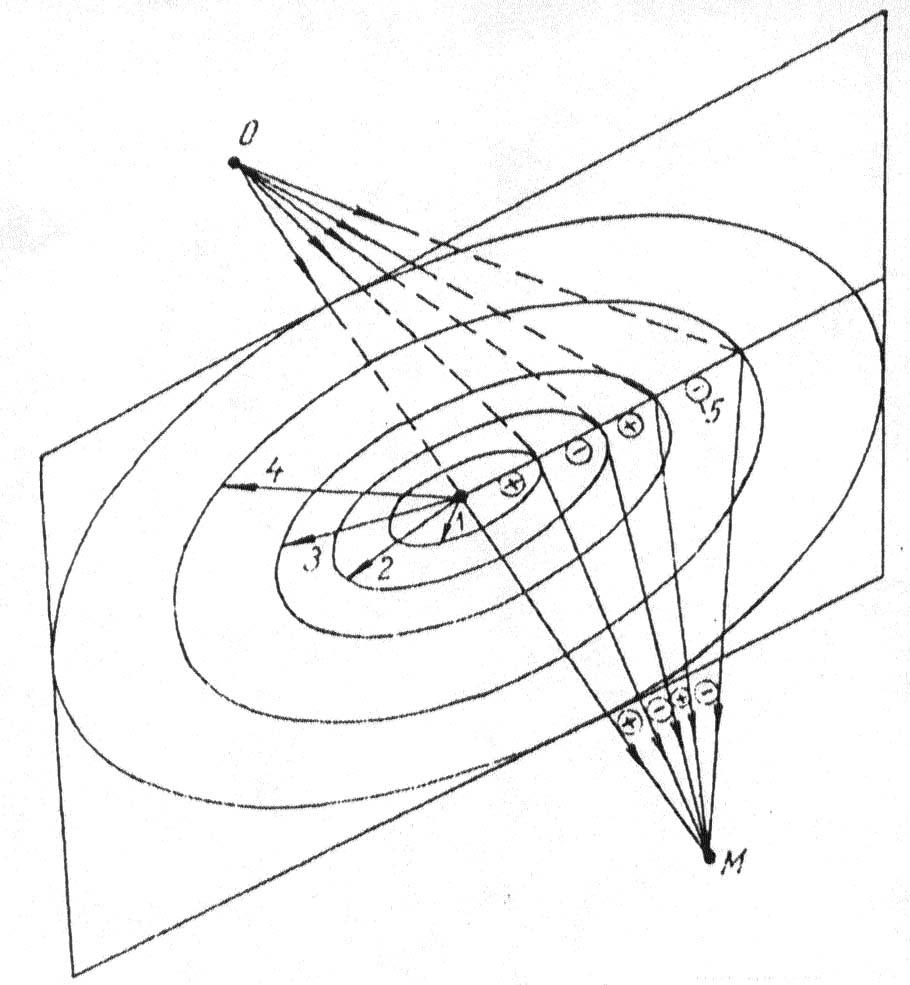
Рис.1.10. Схема расположения зон Френеля: 1, 2, 3, 4 – радиусы зон;
5 – знак зон Френеля ( «+» или «–»)
Таким образом, можно считать, что каждая из зон порождает в точке М знакопеременные колебания. При сложении эффектов от всех зон получается знакопеременный ряд с постоянно убывающими по абсолютной величине членами. Структура этого ряда близка к бесконечной геометрической прогрессии, сумма которой приблизительно равна половине величины первого слагаемого. Поэтому результирующий эффект в точке М будет равен примерно половине воздействия от первой (центральной) зоны Френеля. Радиус круга, площадь которого равна половине площади первой зоны Френеля, будет определяться формулой
R![]() =
=![]() ,
(1.18)
,
(1.18)
где r – расстояние от источника до рассматриваемой плоскости; l – расстояние от рассматриваемой плоскости до точки наблюдения; λ – преобладающая длина волны.
Максимального
значения величина R![]() в однородной среде достигает в середине
пути от источника до приемника:
в однородной среде достигает в середине
пути от источника до приемника:
R![]() =
=![]() .(1.19)
.(1.19)
Именно эта формула позволяет оценить максимальный размер зоны, формирующей передачу энергии относительно плоскости отражения.
