§3. Групповое ранжирование объектов по Парето.

В §2 рассматривался однокритериальный случай сравнения объектов.

Если объекты оцениваются по нескольким разным критериям, то простое ранжирование по каждому критерию приводит к абсурду. Переходим к групповому ранжированию, используя понятие оптимальности по Парето.

Объект O_iстрого предпочтительнейO_k(, доминирует его), если оценкаO_iхотя бы по одному критерию превосходит оценкуO_k, а по всем остальным критериям не хуже оценокO_k. Тогда оптимальным по Парето объектом будет тот, для которого не существует доминирующих объектов. Множество всех таких объектов называетсяпаретооптимальным множеством.

Групповое ранжирование объектов по Парето осуществляется в несколько этапов:

1. На первом этапе выделяется паретооптимальное множество, которому присваивается ранг 1.

2. На втором этапе определяют паретооптимальное подмножество, на множестве, из которого удалена группа объектов первого ранга и этому подмножеству присваивается ранг 2 и т. д., пока не исчерпаем всё исходное множество объектов.

Пример:

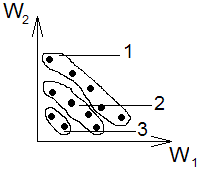
Поскольку ранги объектов определяются не абсолютными, а относительными оценками, то для реализации алгоритма достаточно иметь информацию о типе отношений внутри каждой пары объектов, то есть фактически надо лишь знать для каждой пары, объектов доминирует ли один другого или нет.

Поэтому вводят булеву переменную a_ij=

Пример группового ранжирования по Парето.

Пусть в очереди ОС есть 9 задач, решаемых на ЭВМ. Каждая характеризуется тремя ресурсными показателями W₁,W₂,W₃, гдеW₁– время использования канала ввода/вывода;W₂– время решения задач;W₃– объём занимаемойRAM. Будем считать, что чем больше ресурс, требуемый для решения задачи, тем более срочной является задача (то есть её надо решать раньше).

Требуется ранжировать все 9 задач по «групповой срочности»: группу 1 решать в первую очередь и т.д.

Исходные данные (в условных единицах) приведены в таблице 1.

Таблица 2. - булева матрицаNN.

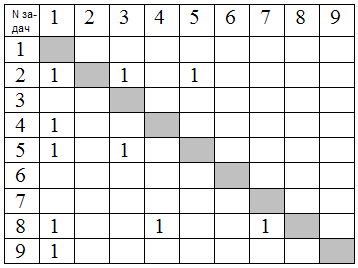
Пустые клетки – «0».

W₁,W₂,W₃max

«1» в некоторой i-й строке определяют объектыO_j, которые объектO_i доминируют, поэтому если вj-ом столбце стоят одни «0», то не существует объекта, который бы доминировал объектO_jи множество всех объектов с «0»-ми столбцами и будет паретооптимальным множеством.

Ранг 1: {2,6,8,9}

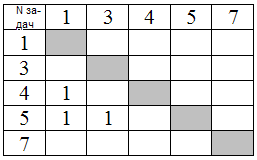
Ранг 2: {4,5,7}

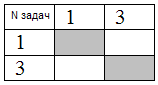
Ранг 3: {1,3}

В первую очередь надо решать задачи {2,6,8}, во вторую {4,5,7}, и в последнюю очередь {1,3}.

§4 Проверка непротиворечивости результатов парных сравнений объектов, проведённых экспертом в шкале отношений и построение вектора приоритетов.

4.1. Собственные векторы и собственные значения матрицы.

,

- в матричном виде.

- вектор-столбец неизвестных;

;

- вектор-столбец правых частей;

;

Квадратная матрица коэффициентов:

А – линейный оператор.

.

Собственный вектор квадратной матрицы А- это такой ненулевой векторW, который удовлетворяет уравнению:(1), т.е. матрицей линейного преобразования он преобразуется в коллинеарный вектор.

Величина , соответствующая такому преобразованию, называетсясобственным значением (числом) матрицы А.

Перенесём в левую часть: (1’)

- единичная матрица.

Система (1’) представляет собой однородную систему линейных уравнений, которая всегда имеет тривиальное решение (W=0). Следовательно, по определению, собственный вектор матрицы А, это такой векторW, который является нетривиальным решением системы (1’).

Из линейной алгебры известно, что для существования нетривиального решения однородной системы линейных уравнений необходимо, чтобы матрица её коэффициентов была вырожденной, т.е. чтобы её определитель был равен нулю.

В данном случае, чтобы выполнялось: (2) – характеристическое уравнение матрицы А. Левая часть – характеристический полином матрицы А.

Имеет место следующее утверждение:ЕслиWкакой-то вектор матрицы А, то любой коллинеарный ему векторесть тоже собственный вектор матрицы А.

Часто, чтобы из этого бесконечного множества собственных векторов выбрать какие-то конкретные в качестве базисных, их нормируют (нормализуют), т.е. делят на какое-то одно и то же число. Часто таким числом выбирают модуль вектора , а для А>0:.

Собственные векторы обладают, среди прочего, одним замечательным свойством:если вn-мерном векторном пространстве выбрать в качестве базиса систему, состоящую изnсобственных векторов, то матрица А линейного преобразования получит следующий диагональный вид:

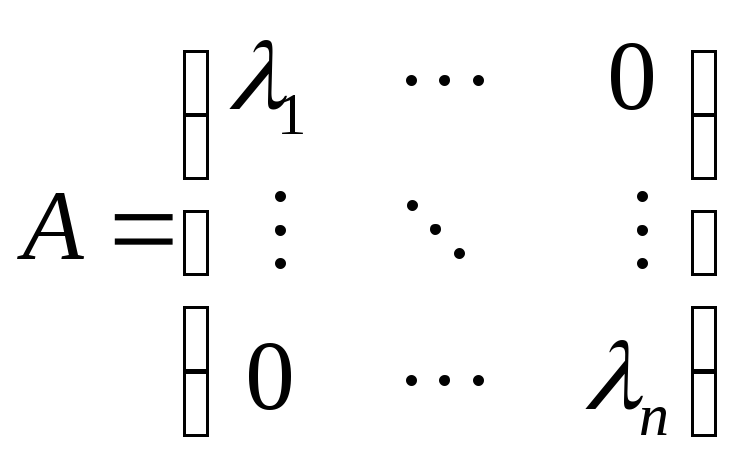(3), где- соответствующие этим собственным векторам собственные числа матрицы А.

Следом матрицы Аназывается сумма её диагональных элементов

(4)

С учётом (3) след можно представить как

(5)

Можно показать, что след k-й степени матрицы А равен

(6).