А . В. Критерій Найквіста у логарифмічній формі
4.8
Критерій Найквіста у логарифмічній формі
В2 |
|
|
|
і |
Пдповідно |
до критерію Найквіста |
про |
стійкість |
|
^замкнутої |
системи можна судити |
не |
тільки за |
\'І»\ розімкнутої системи, а й за взаємним розташуванням амплітуд- ної і ф.і юної частотних характеристик відповідної розімкнутої систе- мі іиичайно при цьому використовують логарифмічні характеристи- і и амплітудну Доз) і фазову ф(со), що пояснюється простотою їх по-
інчиї, Стосовно логарифмічних характеристик критерій стійкості
IIіпі міста (формулюється так:
І»и іц.) ( истема стійка в розімкнутому стані, то для стійкості замкнутої системи не-
•••чідно і достатньо, щоб логарифмічна амплітудна характеристика (ЛАХ) перети- | м піп нісь абсцис раніше, ніж фазова характеристика в останній раз перетинає
'•її(їм» ті, іншими словами, на частоті зрізу со3, яка відповідає /.(со) = 0, фаза за мо- м/мсм має бути меншою за я;
•<і. що с истема нестійка в розімкнутому стані і має к коренів у правій півплощині, і• • для ( пйкості замкнутої системи необхідно і достатньо, щоб при додатній ЛАХ мт,м< іь перетинів фазовою характеристикою рівня -я знизу доверху була на/с/2 і».» і більшою за кількість перетинів у зворотному напрямі.
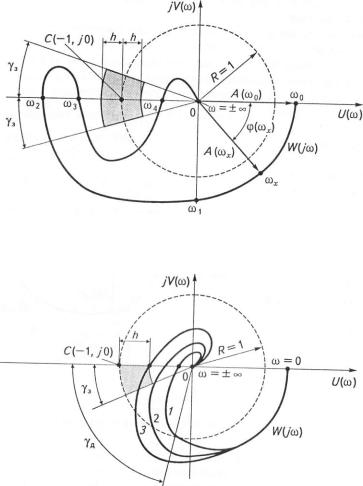
Перше формулювання пояснюється характеристиками, наведе- н и м и і із рис. 4.22. На цьому рисунку зображені ЛАХ Дсо)і чотири варі пі і и фазової характеристики ф(со). Фазові характеристики / і 4 відіі. читають стійкій замкнутій системі, причому характеристика 4 від-
|
інчч і а ( |
АФХ на рис. 4.17, б. Якщо |
|
|
фатма |
|
характеристика має вигляд |
|
|
|
іо |
іамкнута система |
перебуває |
|
|
н і межі ст ійкості, а характеристи- |
|
|
і а |
і иідповідає нестійкій замкну- |
|
|
I НІ системі. |
|
|
|
|
І рафіки характеристик, зобра- |
|
|
жай на рис. 4.23,(3, відповідають |
|
|
мін пі замкнутій системі при к = 1 |
|
|
і І |
' перет ину), а на рис. 4.23 ,5 — |
|
|
нри к |
|
1 (один перетин). |
|
|
|
І ач |
використання |
критерію |
|
|
Н аіїї ик та в логарифмічній формі |
|
|
II н і і.і |
нмі ги будувати ЛАХ і ЛФХ |
Рис. 4.22. |
|
(фанжу) частотні характеристики. |
|
|

Глава 4 |
СТІЙКІСТЬ НЕПЕРЕРВНИХ ЛІНІЙНИХ СИСТЕМ |
|
|
|
|
АВТОМАТИЧНОГО КЕРУВАННЯ |
|
|
|
|
|
|
|
|
|
і |
Ф< |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
СО |
|
|
|
|
0 |
|
Ідсо3]\ |
Ідсо |
|
|
|
|
|
і |
х |
\\ |
|
|
|
|
|
1 |
|
|
3 |
|
|
1 ^^ |
|
|
|
1 |
|
^ |
|
|
|
—71 |
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 423 |
При побудові ЛАХ розімкнутої системи немає сенсу знаходити амплітудну характеристику Дсо) системи і будувати залежність 201§У4(Ш) ВІД 1§(ОО). Я К Щ О система зведена до одноконтурної, то вона складається з ланцюжка послідовно з'єднаних ланок, для яких справедливими є такі співвідношення:
|
( 4 . 3 9 ) |
ф ( Ш ) = Х Ф , ( Ш ) , |
( 4 . 4 0 ) |
де Ц (ш) і фДоо) — відповідно ЛАХ і ЛФХ окремих ланок.
Отже, логарифмічні частотні характеристики розімкнутої системи можна отримати підсумовуванням ординат характеристик окремих ланок. Для побудови ЛАХ розімкнутої системи її передаточну функцію слід подати у вигляді добутку елементарних співмножників, порядок яких не перевищує другий, наприклад у вигляді
Щр) = |
к(Т2р+ |
1) |
р(Т1р+\)(Т3р+ І)(Т42Р2 |
( 4 . 4 1 ) |
|
+ Т5р + 1) |
і скористатися таблицею логарифмічних частотних характеристик елементарних співмножників передаточних функцій (табл. 4.5).
ЛАХ розімкнутої системи зазвичай будують одразу без побудови ЛАХ окремих ланок. Для цього спочатку знаходять точку з координатами Дш)= 201 1 (І£ш= 0), де к — коефіцієнт передачі ро-

А . В. Критерій Найквіста у логарифмічній формі
ЧМІ нутої системи. Потім через знайдену точку проводять пряму з
|
|
|
|
|
н І Ч І М О М |
20(/?7 - г) дБ/дек, де т — кількість диференціювальних ла- |
іі і |
/ |
кількість інтегрувальних ланок. Після |
цього на осі абсцис |
пий |
і,шлють значення частот сполуки |
де |
Т{ — сталі часу еле- |
• і. її іарипх співмножників. Для коливальної ланки це стала часу при
Поряд із значенням 1^(1/7]) |
на осі абсцис зручно вказувати зна- |
п иіім |
частот оо, = 1/7]. Потім |
пряму, яка проходить через точку |
/і« о |
?[) І^/с, со=1, продовжують до найменшої частоти сполуки. В |
ІІІІ з цією частотою змінюють нахил прямої лінії відповідно до ти- м « н-мен гарного співмножника, стала часу якого визначає цю час- > -1 \ ( полуки. Так само характеристика продовжується в бік зростаннм час ют и, зазнаючи послідовні злами на кожній частоті сполуки. За н- «іГімлиості побудовану ЛАХ уточнюють шляхом урахування попра-
• "і |
міч коливальних ланок. |
|
|
|
|
|
|
|
ІФХ визначається як сума фазових характеристик елементарних |
ііінмпожників. Наприклад, для |
передаточної функції (4.41) |
ро- |
і |
«і нуіої системи фазова характеристика будується за рівнянням |
|
|
1 |
|
2 |
|
|
|
5 со |
|
|
|
|
|
|
Т |
|
|
Ф((о) |
-ті/2 - агсі§Г |
со+ агсї§Г |
|
ооагс^Т^ооагсі£ |
1 - Г4 оо . |
|
|
І.<н підження стійкості системи за критерієм Найквіста в лога- |
ічіфмгпііп |
формі виконується в такій послідовності. |
|
|
|
|
і Досліджувана система зводиться до одноконтурного вигляду. |
|
! Записується передаточна функція розімкнутої системи у |
ви- |
і « і її аобутку елементарних співмножників. Співмножники другого
м• ч'•'акV вигляду Т2р2 + Т2р+ 1 або —— |
будуть елементар- |
Т2р |
+ Т2р + 1 |
ними, якщо виконується умова Т2/27] < 1. Якщо ця умова не викопу-
• 11 < |
і, і о співмножник другого порядку слід подати у вигляді добутку |
їй |
івмножників першого порядку: |
|
|
|
|
Т2р2 |
+ |
Т2р + |
1 |
= (ТАр + |
1)(Твр + |
1); |
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Т2р2 |
+ |
|
Т2р+ |
1 |
(ТАр+ |
1)(Твр + |
1)' |
/їм
т1 Л, В - - Т і ї 0 Ш -4Г'2
Глава 4 |
СТІЙКІСТЬ НЕПЕРЕРВНИХ ЛІНІЙНИХ СИСТЕМ |
|
АВТОМАТИЧНОГО КЕРУВАННЯ |
Для розкладання співмножників третього порядку 7]3р2, |
+ Т2р2 + |
+ Т3р + 1 або 1/(Т^р3 + Т2р2 + Т3р+ 1)на елементарні треба |
будь - яким |
із відомих способів (наприклад, за формулами Кардана або способом наближеного розв'язку рівнянь високого порядку) визначити корені рівняння
Г,У + ТІР2 + ТіР+ 1 = 0.
Якщо корені рівняння дійсні та різні (рх =-Х)-,р2 = -Х2 ; р} = -Х3), то співмножник третього порядку подається у вигляді трьох елемен-
тарних співмножників першого |
порядку: |
|
7]У + Т2 р2 +Т,р+ 1 = |
р+ 1 |
р+\ |
р + 1 |
V*. |
ч х 2 |
ЧХ3 |
|
|
1 |
|
Т\ Р + Т2 Р + 7 > + 1 |
Р+1 |
/>+1 |
Р+1 |
|
Якщо ж рівняння має один дійсний корінь р{ = -X! і два ком плексних р2 = -а + /?3 = -ос - то співмножник третього порядку подається у вигляді добутку двох співмножників — першого і другого порядку:
7] У + Т2 р2 + Тгр + 1 |
_1_ р+1 |
1 |
У + |
2 а |
-/>+1 |
|
|
а 2 + |
р - |
а 2 + р |
|
717» + ТгР + 1 |
|
1 |
|
2 а |
|
V А : |
|
а 2 + р: У + а 2 |
+Р : |
|
Аналогічно можна розкласти на елементарні також співмножники більш високих порядків. У цьому разі задача ускладнюється, оскільки виникає необхідність знаходити корені рівнянь більш високих порядків. Такі співмножники можна отримати у разі приведення складних багатоконтурних систем з перехресними зворотними зв'язками до одноконтурних. Тому для дослідження таких систем критерій Найквіста в логарифмічній формі, як правило, не застосовують.
4.8.Критерій Найквіста у логарифмічній формі
3.Перевіряється стійкість розімкнутої системи на основі рекомендацій, наведених при викладенні методики дослідження стійкості критерієм Найквіста у звичайній формі. Якщо розімкнута система нестійка, то визначається кількість коренів у правій напівплощині. Оскільки попередньо передаточна функція розімкнутої системи подана у вигляді добутку елементарних співмножників, то при дослідженні стійкості розімкнутої системи ускладнень не виникає.
4.Будується ЛАХ розімкнутої системи за раніше викладеними правилами і за даними табл. 4.5.
5.Записується рівняння фазової характеристики у вигляді суми фазових характеристик елементарних співмножників, обчислюються значення ф(оо)за різних частот со, будується фазова характеристика.
При розрахунках фазових характеристик для співмножників другого порядку досить часто припускаються помилок при визначенні кутів, які перевищують за абсолютною величиною 90°. Щоб уникнути можливих помилок, необхідно мати на увазі, що для коливальної ланки з передаточною функцією \/(Т2р2 +Т2р+ 1) фазова характеристика розраховується за формулою
Г9со
ф= - а г с 1 8 " Г ^ -
Уразі збільшення частоти від 0 до 1/7] значення ф(со) змінюється від 0 до -90°. При частоті со > 1/7] вираз Г2са/(1 - 7]2со2 )стає від'ємним і
Ф = +агсі£ |
Г7 со |
1 - 7 > 2 |
У цьому разі значення кутів слід вибирати не в першій чверті (від 0 до +90°) , а в третій (від -90° до -180°). Наприклад, якщо
^ - 0,364, 7]2со2 - 1
чому відповідає кут у першій чверті а = 20°, то ф(со)слід визначати за формулою
Ф(со) = — 180° + а = -160°.
Для співмножника Т2Р2 + Т2Р+ 1 фазова характеристика
ф(со) = +агсі£ |
Т2 со |
1 - 7]2со2 |
Н Теорія а в т о м а т и ч н о г о к е р у в а н н я |
225 |
|

Глава 4 |
СТІЙКІСТЬ НЕПЕРЕРВНИХ ЛІНІЙНИХ СИСТЕМ |
|
АВТОМАТИЧНОГО КЕРУВАННЯ |
При 0 < со< 1/7] значення кутів треба вибирати в першій чверті в інтервалі від 0 до +90°, а при ш> 1/7], коли
7| ю - 1
— у другій чверті в межах від +90° до +180°. Нехай Г2со/(7]2со2 - 1) =
= 0,364, тоді ф(ш)= +180° |
- 2 0 ° |
=+160°. |
Якщо ЛАХ і ЛФХ побудовано правильно, то граничне значення |
фазової характеристики |
при |
має відповідати граничному на- |
хилу амплітудної. Отже, якщо граничний нахил амплітудної характеристики (п - т)20 дБ/дек, то граничне значення фазової характеристики (п - тде /7, т — порядки поліномів відповідно знаменника і
чисельника передаточної функції розімкнутої системи.
Наприклад, якщо граничний нахил ЛАХ дорівнює -60 дБ/дек, то граничне значення фазової характеристики має становити -270°.
6. За взаємним розташуванням ЛАХ і ЛФХ розімкнутої системи робиться висновок про стійкість замкнутої системи.
• П р и к л а д 4.6. Передаточна функція розімкнутої системи має вигляд
Щр) = №л(р)]Ув{р))¥с(р) =
40(0,02 р+ 1)(0,1/;+ 1)(0,5/;+ 1)
~ (0,04/У + 0,2/;+ 0(2,5/;+ 0(0,05/;+ 1)'
Дослідити стійкість системи за допомогою критерію Найквіста в логарифмічній формі.
Р о з в ' я з а н н я . Визначимо, чи є поліном другого порядку у знаменнику передаточної функції елементарним. Коренями поліному 0,04/;2 + 0,2/; + 1 є р{ 2 = - 2,5 ± у'4,33. Вони комплексні, тому співмножник 1/(0,04/г + 0,2/; + 1) є елементарним і вираз передаточної функції розімкнутої системи залишається без змін. ЛАХ розімкнутої системи будуємо у такій послідовності.
1. Через точку з координатами Дсо) = 20 1§ 40 = 32 дБ, 1§ ш = 0(оо = 1) проводимо горизонтальну лінію (нахил 0), тому що розімкнута система не містить інтегрувальних і диференціювальних ланок (передаточна фу-
нкція |
розімкнутої системи не містить співмножників р і 1 /р). |
2. |
Розраховуємо логарифми частот сполуки: |
А . В. Критерій Найквіста у логарифмічній формі
18033 = 1^ = 0,3; |
1^ = 1 8 - ^ |
= 0,7; |
І8оз5 = І 8 ^ = -0,4; |
18 со6 = |
= 1,3 |
і підкладаємо їх на осі абсцис.
|
|
|
|
|
3. |
Продовжуємо побудовану в п.1 |
пряму до найнижчої частоти |
сполуки со5 |
= 1/2,5. Стала часу 2,5 належить елементарному співмножни - |
ку 1/(2,5/; + |
1), тому в точці зламу нахил ЛАХ змінюється на - 2 0 д Б / д е к і |
і і а п о в и т ь |
0 + (—20) = —20 д Б / д е к . Лінія |
з нахилом - 2 0 д Б / д е к |
прово - |
щіться |
паралельно прямій, що з'єднує точку Дсо) = 20 дБ на осі |
орди- |
п.і г { |
кіпцем першої декади. На частоті оо3 = 1/0,5 відбувається другий |
імам характеристики. Її нахил становитиме - 2 0 + 20 = 0 д Б / д е к , бо статі часу 0,5 належить співмножнику (0,5/; + 1). Наступний злам відбува-
< |
н.си на частоті со, = |
1/0,2, яка визначається співмножником 1/(0,04/^ + |
і |
0,2/;+ 1) = 1/(0,22/г + |
0,2/;+ 1), тому |
нахил характеристики змінюється |
па - 4 0 д Б / д е к і становить 0+ (-40) = |
- 4 0 д Б / д е к . |