Teoriya avtomatichnogo keruvannya

3 . 1 3 . Гоафи та їх використання в теорії автоматичного керування

Ліквідувавши перехрещення зворотних зв'язків, нескладно спро- ( і и ї й одержані структурні схеми за раніше викладеними правилами і наведеними формулами.

3.13

Графи та їх використання

втеорії автоматичного керування

Загальні відомості про графи. Математичну модель си- і іеми автоматичного керування можна дістати також за допомогою орієнтованих графів.

У загальному випадку під графом розуміють деяку множину то- чок М, які називають вершинами, і множину непересічних кривих — ребер К, що відповідають умовам:

•кожне ребро К має рівно дві точки множини М, які є граничними точками ребра (ребро в цьому разі називають незамкнутим);

•замкнуте ребро має тільки одну точку з множини М (граничні точки збігаються);

•ребра Я не мають інших спільних точок, окрім тих, які входять

умножину М.

Якщо на ребрах вказано напрям переміщення, то відповідний

іраф називають орієнтованим, а ребро орієнтованого графа — дугою.

Іраничні точки ребра є вершинами. Вважають, що саме ребро К шцидентне кожній з вершин, а кожна вершина інцидентна цьому ребру.

Узагальному вигляді граф позначається буквою Сабо (/?, А/), де і< множина ребер; М — множина вершин.

Якщо якийсь граф = /(А/,, К{), де М\ та К{ входять до множин М і /?, з яких складається граф С, то граф С^ називають підграфом ірафа С (або підграфом (7), який, своєю чергою, називають надграфом графа С1 (або надграфом 0{).

Граф зі скінченною кількістю вершин і ребер називають скінченним. На кожній дузі є початкова і кінцева вершини.

Згідно з викладеним орієнтований граф є сукупністю множин вершин і дуг. Дуги називають паралельними, якщо вони мають

• пільні початкові і кінцеві вершини. З'єднання дуг, за якого кінцева

151

вершина кожної дуги є початковою вершиною для наступної дуги, називають орієнтованим маршрутом. Якшо кінцева вершина останньої дуги збігається з початковою вершиною першої, то такий марш-

рут називають замкнутим.

Орієнтований маршрут, в якому всі дуги різні, називають шляхом від початкової до кінцевої вершини (при незамкнутому стані). Якщо цей маршрут замкнутий, то його називають контуром або орієнтованим циклом.

Основні властивості графів САК іметодика їх побудови.

Граф системи автоматичного керування є орієнтованим графом, що має такі властивості:

•кожна дуга відображає ланку системи з відповідним математичним зображенням;

•якщо до вхідної (початкової) вершини деякої дуги приєднуються (входять в неї) кілька дуг, то відповідна вхідна змінна є сумою вихідних величин цих дуг. При одній приєднуваній дузі змінна, що їй відповідає, є вхідною змінною наступної дуги (її вершини);

•якщо з кінцевої вершини виходять кілька дуг, то вхідна величина всіх дуг є однаковою.

Граф САК легко побудувати, якщо відома структурна схема системи. Якщо відомий граф, то нескладно побудувати структурну схему відповідної системи. Вершини графа зображуються колами.

При побудові графа за структурною схемою необхідно виконати такі перетворення.

1.Зобразити схему таким чином, щоб у суматорах усі вхідні величини мали знак плюс.

2.Кожний суматор замінити вершиною з вхідною величиною, що дорівнює вихідній вершині цього суматора.

3.Кожну ланку структурної схеми замінити дугою з оператором (передаточною функцією), який дорівнює оператору цієї ланки.

4.Кожній змінній, в тому числі й збуренню, поставити у відповідність свою вершину.

5.Додаткове зображення (якщо це потрібно) вершини однієї з дуг на загальному вході деякої дуги провести з урахуванням одиничної передаточної функції.

152

3.13. Гоафи та їх використання в теорії автоматичного керування

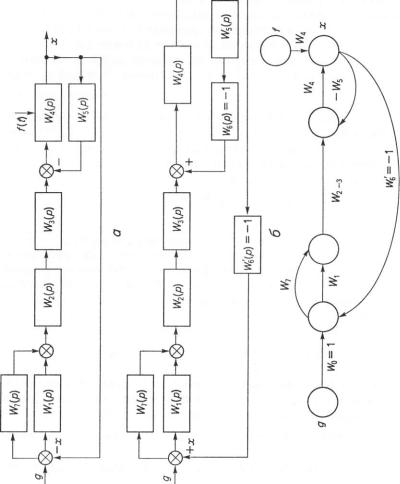
Деяку вихідну структурну схему слідкувальної САК показано на рік 3.39, о, а змінену структурну схему згідно з п. 1 — наведено на

рис 3.39, б.

Кінцевий результат — відповідний граф САК, наведено на

рис. 3.39, в.

Мри побудові графів можливе їх спрощення, яке досягається за рахунок того, що паралельні дуги можна замінити однією дугою з передаточною функцією, яка дорівнює сумі передаточних функцій цих дуі І Іростий шлях (якщо немає не належних до нього дуг, інцидентних його проміжним вершинам) можна замінити дугою з передаточ- ною функцією, що дорівнює добутку передаточних функцій дуг цьоіо шляху.

Знаходження передаточної функції САК за допомогою і/юрмулиМейсона. Формула Мейсона використовується для спрощення графа та знаходження передаточної функції замкнутої системи ппоматичного керування за відомим графом системи.

Формулу записують у вигляді

де £ — вхідна, а х — вихідна величини системи (графа); \¥1 (р)— передаточна функція /-го простого шляху від вершини £ до вершини х, що дорівнює добутку передаточних функцій дуг, які належать цьому шляху (контуру); т — кількість таких шляхів (для спрощення запису передаточних функцій далі не писатимемо знак оператора р)\ А — визначник графа.

Записується визначник графа у вигляді

А = 1 - + З Х о Л " . . . ,

Мі хі

ае \¥{)] — передаточна функція у-го простого контуру, яка дорівнює добутку передаточних функцій всіх дуг даного контуру. Перший член є сумою всіх подібних простих контурів. Другий член

V М/[)іН/()к — сума пар контурів у та к, що не стикаються з іншими /,А

і оптурами (И/Г0к — результуюча передаточна функція контуру /с, по-

сума добутків передаточних функцій відповідних контурів; їх дода

153

"Н

Ої

"і

о

со о.

154

3 . 1 3 . Гоафи та їх використання в теорії автоматичного керування

пні. по трійці контурів, що не стикуються. Аналогічно можна обчис- тим пі й інші члени, якщо вони є в даному складному графі. При н ь о м у треба мати на увазі, що контурами, що не стикуються, назива- но і. і акі два контури, які не мають спільних дуг або вершин. Трійка, ч»' і нірка і так далі контурів вважається такою, що не стикується, як- що будь-яка пара контурів цієї трійки (четвірки і т. д.), своєю чер- пни, не стикується; Д/ — детермінант підграфа, який можна дістати з і о мовного (вихідного) графа при виключенні дуг і вершин /-го прос- ино шляху, а також дуг і вершин, інцидентних цим вершинам.

Запишемо передаточну функцію системи автоматичного керуиаііня за завданням £ згідно з формулою Мейсона відповідно до риє 3.39 (при цьому вважатимемо / = 0). З рис. 3.39, в видно, що від першини £ до вершини х є два (І і II) прості шляхи з такими переда- І О Ч П П М И функціями:

IVі =Ж0Ж1И/2_3Ж4 =И/РК2_3Ж4;

ЖП = ^ 0 ^ 7 ^ 2 - 3 ^ 4 = ^ 7 ^ 2 - 3 ^ 4 - Крім цього, у вихідному графі є три контури (позначимо їх 1,

\передаточні функції яких

11 ар і контурів, що не стикуються, граф не має, тому його визнач-

ник

І Іідграфи, які відповідають простим шляхам від вершини £ до х, іамкнутих контурів не мають, тому

Якщо погрібно знайти передаточну функцію за збуренням, то враховують, що £ = 0 . При цьому від вершини / до і маємо лише

155

має замкнутих контурів і його визначник дорівнює одиниці: Д, = 1. Передаточна функція за Мейсоном матиме вигляд

3.14

Багатовимірні системи та метод змінних стану

Багатовимірні системи і загальні відомості про метод змінних стану. В САК у загальному випадку можна одночасно керувати кількома величинами. Як було зазначено раніше, такі системи

називають багатовимірними.

Багатовимірні системи називають також системами багатозв'язного керування. Ці терміни переносять і на відповідні об'єкти (наприклад, багатовимірний об'єкт). Класичним прикладом багатовимірного об'єкта є паровий котел, в якому одночасно автоматично керують температурою і тиском пари.

Лінійними багатовимірними системами називають системи авто-

матичного керування, в яких усі елементи мають лінійні характеристики і їхні динамічні властивості описуються лінійними диференціальними рівняннями. Якщо коефіцієнти цих рівнянь незмінні, то таку систему називають стаціонарною (в противному разі — неста-

ціонарною).

Рівняння багатовимірної системи в загальному випадку можна записати у вигляді системи рівнянь в операторній формі:

156

3.14. Багатовимірні системи та метод змінних стану

+ САР)А + • • • + с„к (р)/к.

V компактнішій формі це рівняння можна записати так:

1(1 (/'), (/?)> с, (/?) — поліноми від р зі сталими коефіцієнтами при відповідних регульованих змінних х{,..., хп\ щ,..., ит — керуючі сигпани; /,, ... ,/* — збурення.

Для багатовимірних систем найпоширенішою є матрична форма єн і псу рівнянь, згідно з якою в даному разі введемо такі матриці:

І Іри цьому вихідну систему рівнянь багатовимірної системи можна записати у вигляді

А(р)х = В(р)и + С{р)і.

•Приклад 3.4. Деяка двовимірна система описується рівняннями

( 7 > + 1)х, + (Т2р+ \)Х2 = Ь0ри{ + Ь{и2;

Записати рівняння цієї системи в матричній формі.

Р о з в ' я з а н н я . Рівняння цієї системи в матричній формі матиме вигляд

157

Передаточною функцією за деяким /-м параметром та к-м виходом називають відношення зображення за Лапласом Хк (з) вихідного параметра хк до зображення І]Д^) вхідної величини иі за нульових початкових умов. Згідно з цим

вд

Обчислити цю передаточну функцію можна, якщо знехтувати у вихідній системі рівнянь зображеннями всіх сигналів і параметрів керування, крім И{ (я).

Аналогічно можна знайти також передаточну функцію за збуренням відповідно до цього виходу (параметра хк)\

ЗД

Для повного описання багатовимірних систем потрібно мати пхт передаточних функцій за керуванням і пх к передаточних функцій за збуренням, які в загальному вигляді можна записати як матриці:

IVй (5) =

и а д ...

де IV"(з) — матриця передаточних функцій за керуванням (або передаточна матриця); IV/ (з) — передаточна матриця за збуренням.

Зображення керованого параметра х через передаточні матриці матиме вигляд

Х(з) = №и(з)и(з) + Ц^/(з)Р(з).

Розглянемо спосіб визначення передаточних матриць, що базується на відомих співвідношеннях, які наведемо без доведення:

IVй(з) = Л1 (*) В(з)\ IV'(з) = А'1 (з)С(з).

При нульових початкових умовах А(р) = А(з); В(р)=В(з);

С(р) = С(з).

158

3.14. Багатовимірні системи та метод змінних стану

ііідио з положеннями вищої алгебри обернену матрицю визна-

Знак т означає операцію транспонування.

І Іроілюструємо викладене за допомогою простого прикладу.

и П р и к л а д 3.5. Маємо двовимірну систему, поведінка якої визначається двома диференціальними рівняннями

р2хх + рх{ + = щ + Уі; рх{ + х, + рх2 = и2 + /2.

Необхідно знайти передаточні матриці за керуванням и і збуренням /

Р о з в ' я з а н н я . Запишемо наведені вище рівняння в формі зображення Лапласа:

(л- о в д + зХ2(з) = 1/2(з)+Г2(з).

Ця система в матричній формі матиме вигляд

>Ф)Х(у) = В(з)ЩЗ) + С(З)¥(З),

де

Знайдемо визначник матриці

1) = з2(з + 1) - (5 + \) = (з2-з)(з + 1).

Переставивши по діагоналі складові матриці А(з) та змінивши знаки елементів із непарною сумою індексів, дістанемо

5-(5+1)"

-1 5 2 + 5

IVЙ (З) = Ц"(5) = А-\З) =

159