3.Найти основные периоды для периодических функций

2. Предел функции

В математическом анализе рассматриваются функциональные зависимости двух или более переменных. Особый интерес представляет изучение поведения функции при упорядоченном изменении независимой переменной, т.е. предельный переход, который является одной из основных операций математического анализа. Понятие предела является базой, на которой строится классическое учение о функциях. Выясним сначала это понятие применительно к числовым последовательностям.

2.1. Числовая последовательность. Предел числовой последовательности

а) Рассмотрим некоторую функцию натурального аргумента, а именно функцию f(n), определенную на множестве всех натуральных чисел.

1, 2, 3, 4, ..., N, ...

Определение. Всякая функция у=f(п), заданная на множестве всех натуральных чисел, называется (бесконечной) числовой последовательностью.

Закон соответствия f сопоставляет каждому натуральному числу п определенное значение функции f(п)

f(1), f(2), f(3), ..., f(п), ...

Значение функции удобно обозначать одной буквой, снабженной индексом (значком), указывающим, какому натуральному числу соответствует взятое значение функции f(п)

у₁= f(1), у₂=f(2), у₃=f(3), ..., у_п=f(п), ...

Числа у₁, у₂, у₃, ..., у_п, ... называют членами последовательности, член у_п, стоящий в последовательности на п-ом месте, называется п-ым ее членом.

Числовую последовательность обозначают символом {y_n}.

Графиком числовой последовательности является множество изолированных точек.

Чаще всего последовательность задается аналитическим способом, т.е. при помощи формулы у_п=f(п).

Примеры числовых последовательностей.

1)

Члены последовательности

2)

Члены последовательности

б) Виды числовых последовательностей.

Определение. Числовая последовательность {y_n} называется монотонно возрастающей, если при всех натуральных значениях n выполняется неравенство

y_n+1>y_n

У монотонно возрастающей последовательности каждый последующий член больше предыдущего.

Определение. Числовая последовательность {y_n} называется монотонно убывающей, если при всех натуральных значениях п выполняется неравенство

y_n+1<y_n

Определение. Последовательность {y_n} называется ограниченной, если можно указать такое положительное число М, что при всех натуральных значениях п имеет место неравенство

|y_n|<M

Определение. Последовательность называется неограниченной, если для любого положительного числа М имеет место неравенство

|y_n|>M

в) Предел числовой последовательности.

Рассмотрим последовательность:

Изобразим члены последовательности точками прямой

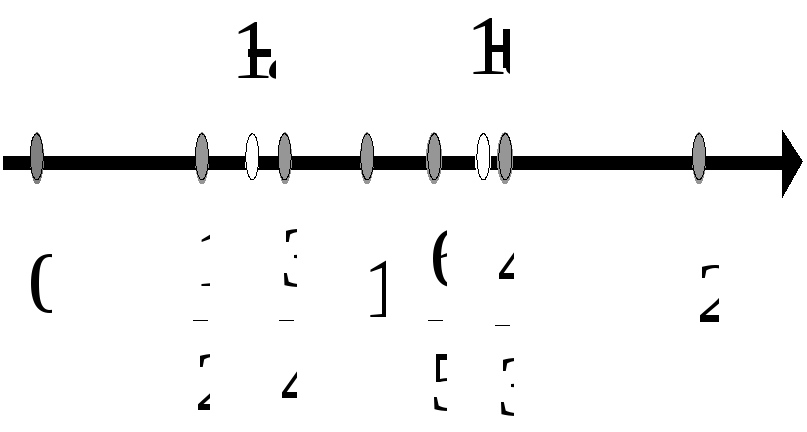
Из рисунка видно, что точки, изображающие члены последовательности, с увеличением номера п все ближе и ближе подходят к точке 1, они как бы "накапливаются" около единицы.

Возьмем любое положительное число . Изобразим на прямой отрезок длиной 2 с центром в точке 1. Очевидно, что точки, изображающие члены последовательности, попадут в интервал (1, 1+) только тогда, когда расстояние между ними и точкой, изображающей единицу, будет меньше . Как известно, расстояние между точками числовой прямой выражается числом

|y_n –1|, независимо от того, будет ли точка у_п слева или справа от точки 1.

Число 1, по отношению к которому члены взятой последовательности {y_n} обладают указанным свойством, называется пределом этой последовательности.

Очевидно также, что с ростом номера члена числовой последовательности, все члены числовой последовательности попадут в интервал (1, 1+).

Определение. Число А называется пределом последовательности {y_n}, если для любого положительного числа  существует такое натуральное число N, что все значения y_n , у которых номер п>N, удовлетворяют неравенству

|y_n–А|<

Тот факт, что А является пределом последовательности записывают так:

Еще одна графическая иллюстрация понятия предела

Интервал (А-, А+) образует –полосу. Все точки, которым соответствуют члены числовой последовательности, у которых номер n>N, попадут в –полосу.

г) Свойства пределов последовательностей.

Теорема Последовательность {y_n} может иметь лишь один предел

Теорема Последовательность, имеющая предел, является ограниченной.