-
Индексы средних величин: индексы переменного и постоянного составов, структурных сдвигов, их использование в анализе. Взаимосвязь индексов.
Для изучения динамики качественных показателей (цена, себестоимость, производительность труда, средняя заработная плата и т. д.) определяют изменение средней величины индексируемого показателя, которое обусловлено взаимодействием двух факторов:
· изменение значения индексируемого показателя у отдельных групп единиц;
· изменение структуры явления.
Для определения влияния каждого из этих факторов на общую динамику средней применяются индексы переменного, постоянного (фиксированного) состава и индекс структурных сдвигов.
Индексом переменного состава является индекс, отражающий соотношение средних уровней изучаемого явления, относящихся к разным периодам.
Рассмотрим индекс цен переменного состава:
.
Отражает соотношение средней цены товаров в текущем и базисном периодах.
Поскольку
средняя цена товаров определяется по
формуле средней арифметической взвешенной
как отношение товарооборота к объему
продаж (
,
),
то индекс цен переменного состава может
быть записан следующим образом:
.
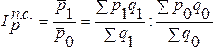Если от объемов товара в натуральном выражении перейти к их удельным весам, то данный индекс может быть записан так:
где 
–
доля каждого товара соответственно в
базисном и отчетном периодах.
Индекс постоянного (фиксированного) состава – характеризует динамику средней величины при одной и той же фиксированной структуре. Индекс постоянного состава показывает, как в отчетном периоде по сравнению с базисным изменилось среднее значение показателя по какой-либо однородной совокупности за счет изменения только самой индексируемой величины, т. е. когда влияние структурного фактора устранено.
Индекс цен фиксированного состава:
или 
–
индекс цен фиксированного состава.
Индексом структурных сдвигов называется индекс, характеризующий влияние изменения структуры изучаемого явления на динамику среднего уровня изучаемого явления.
Индекс цен структурных сдвигов:
или 
–
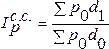индекс цен структурных сдвигов.
Взаимосвязь: 
.
Помимо мультипликативной модели, на основе индексов переменного, постоянного состава и структурных сдвигов может быть построено аддитивное разложение, отражающее абсолютное изменение среднего уровня качественного показателя за счет отдельных факторов.
Так, например, общий абсолютный прирост (уменьшение) средней цены товаров в целом по совокупности находится как разность числителя и знаменателя индекса цен переменного состава:
или 
.
Абсолютный прирост (уменьшение) средней цены за счет изменения цен по отдельным единицам совокупности (например, по отдельным рынкам) определяется как разность числителя и знаменателя индекса цен фиксированного состава:
или 
.
Абсолютный прирост (уменьшение) средней цены за счет структурных изменений рассчитывается как разность числителя и знаменателя индекса цен структурных сдвигов:
или 
.
Общий прирост результативного показателя должен быть равен сумме приростов за счет каждого из факторов. Аддитивное разложение имеет вид:
.
Пример 2: Имеются следующие данные о продаже картофеля на рынках города:
Таблица 7.3
Данные о продаже картофеля на рынках города
|
Рынок |
Базисный период |
Отчетный период |
||
|
Цена за 1 кг, руб. |
Продано, ц |
Цена за 1 кг, руб. |
Продано, ц |
|
|
|
|
|
|
|
Определить индекс цен переменного состава, индекс цен фиксированного состава и индекс цен структурных сдвигов. Сделать выводы по результатам расчетов.
Решение:
1) Индекс цен переменного состава:
,
таким образом, в отчетном периоде по
сравнению с базисным средняя цена
картофеля по рынкам города увеличилась
на 15,8 %;
2) Индекс цен фиксированного состава:
–
за
счет изменения цен на картофель на
отдельных рынках средняя цена в отчетном
периоде по сравнению с базисным
увеличилась на 16,8 %;
3) Индекс цен структурных сдвигов:
,
то есть за счет изменения долей отдельных
рынков в их общем объеме продаж (или за
счет структурных сдвигов) в отчетном
периоде по сравнению с базисным средняя
цена картофеля снизилась на 0,8%.
Пример 3: Продукт А производится на двух предприятиях региона:
Таблица 7.4
Данные о себестоимости и физическом объеме выпуска продукта А предприятиями региона
|
№ предприятия |
Себестоимость за единицу продукта, долл. США |
Физический объем выпуска, тыс. шт. |
||
|
Базисный
период |
Отчетный
период |
Базисный
период |
Отчетный
период |
|
|
|
|
|
|
|
Определить:
1) изменение средней себестоимости продукта А в процентах и в абсолютном размере;
2) абсолютное изменение средней себестоимости за счет действия отдельных факторов:
а) изменения себестоимости по отдельным предприятиям;
б) структурных сдвигов в общем объеме выпуска продукции.
Решение:
1) Определим удельные веса каждого предприятия в производстве продукта А в отчетном и базисном периодах:
Таблица 7.5
Расчетная таблица
|
№ предприятия |
Физический объем выпуска, тыс. шт. |
Удельный вес выпуска, % |
||
|
Базисный
период |
Отчетный
период |
Базисный
период |
Отчетный
период |
|
|
|
|
|
0,308 0,692 |
0,452 0,548 |
|
Итого |
|
|
1,000 |
1,000 |
2) Изменение средней себестоимости в процентах характеризует индекс себестоимости переменного состава:
.
Абсолютное изменение средней себестоимости:
долл.
США.
Средняя себестоимость продукта А в отчетном периоде по сравнению с базисным увеличилась на 3,1%, или на 1,93 долл. США;
3) а) Абсолютное изменение средней себестоимости за счет изменения себестоимостей по отдельным предприятиям можно определить, если из числителя индекса фиксированного состава вычесть знаменатель:
долл.
США.
За счет изменения себестоимости продукта А на отдельных предприятиях средняя себестоимость снизилась на 0,81 долл. США;
б) Абсолютное изменение средней себестоимости за счет структурных сдвигов в общем объеме производства можно определить, если из числителя индекса структурных сдвигов вычесть знаменатель:
долл.
США.
За счет изменения долей отдельных предприятий в производстве продукта А (или за счет структурных сдвигов общем объеме выпуска) его средняя себестоимость увеличилась на 2,74 долл. США.
Взаимосвязь:
;
1,93 = –0,81 + 2,74.
Разновидностью относительных величин является территориальный индекс, т. е. сравнение показателей, относящихся к разным территориям.
Пример: Товарооборот регионов А и В, база сравнения регион В.
, 
,
тогда 
.