Примеры решения задач

Пример 1. Два точечных заряда 9Q и —Q закреплены на расстоянии / = 50 см друг от друга. Третий заряд Qi может перемещаться только вдоль прямой, проходящей через заряды. Определить положение заряда Q\, при котором он будет находиться в равновесии. При каком знаке заряда Qi равновесие будет устойчивым?

_T^S

Решение. Заряд Q\ находится в равновесии в том случае, если геометрическая сумма сил, действующих на него, равна нулю. Это значит, что на заряд Q\ дол­жны действовать две силы, равные по модулю и проти­воположные по направлению. Рассмотрим, на каком из трех участков /, //, /// (рис. 10) может быть выполнено это условие. Для определенности будем считать, что заряд Q\ — положительный.

Рис. 10

На участке / (рис. 10, а) на заряд Qi будут дей­ствовать две противоположно направленные силы: Fi и F2. Сила Fi, действующая со стороны заряда 9Q, в любой точке этого участка больше силы F2, действующей со стороны заряда — Q, так как больший заряд 9Q находится всегда ближе к заряду Qi, чем меньший

74

75

(по модулю) заряд —Q. Поэтому равновесие на этом участке невозможно.

На участке // (рис. 10, б) обе силы Fi иF2 направ­лены в одну сторону — к заряду —Q. Следовательно, и на втором участке равновесие невозможно.

На участке /// (рис. 10, в) силыFi иF₂ направлены в противоположные стороны, так же как и на участке/, но в отличие от него меньший заряд —Q всегда нахо­дится ближе к зарядуQ\, чем больший заряд9Q. Это значит, что можно найти такую точку на прямой, где силыFi иF2 будут одинаковы по модулю, т. е.

Fi = F₂. (1)

Пусть х и I -\- х — расстояние от меньшего и боль­шего зарядов до зарядаQ\. Выражая в равенстве (1)F\ иF₂ в соответствии с законом Кулона, получим9Q Qi/(/ +xf= Q Q]/x², или / +x =± Зх, откуда

*i = +1/2, x₂=- 1/4.

Корень Х2 не удовлетворяет физическому условию задачи (в этой точке силыFi иF₂ хотя и равны по модулю, но сонаправлены).

Определим знак заряда Q\, при котором равновесие будет устойчивым. Равновесие называется устойчивым, если при смещении заряда от положения равновесия возникают силы, возвращающие его в положение равно­весия. Рассмотрим смещение зарядаQ\ в двух случаях: когда заряд положителен и отрицателен.

Если заряд Qi положителен, то при смещении его влево обе силыF\ иFi возрастают. Так как силаF\ воз­растает медленнее, то результирующая сила, действую­щая на зарядQ\, будет направлена в ту же сторону, в которую смещен этот заряд, т. е. влево. Под действием этой силы зарядQ\ будет удаляться от положения равно­весия. То же происходит и при смещении зарядаQi вправо. СилаF₂ убывает быстрее, чемFi. Геометриче­ская сумма сил в этом случае направлена вправо. Заряд под действием этой силы также будет перемещаться вправо, т. е. удаляться от положения равновесия. Таким образом, в случае положительного заряда равновесие является неустойчивым.

Если заряд Q\ отрицателен, то его смещение влево вызовет увеличение силFi иF2, но силаFi возрастает медленнее, чемF2, т. е.|F2l>|Fi|. Результирующая сила будет направлена вправо. Под ее действием зарядQi

76

возвращается к положению <Ь

равновесия. При смещении Q\ /i\

вправо сила F₂ убывает быст- /I \

рее, чем Fi, т. е.|Fi|>|F₂|, ре- _/ \

зультирующая сила направле- /л, \

на влево и заряд Qi опять бу- (y^Q^^ \

дет возвращаться к положе- hay^ri ^^Х^УЛ

нию равновесия. При отрица- /Qyi" ~_г ^

тельном заряде равновесие яв- ^i^-Zrh ляется устойчивым. Величина самого зарядаQ\ несущест- Рис. 11

венна.

Пример 2. Три точечных зарядаQ\ = Q2 = <2з = 1 нКл расположены в вершинах равностороннего треугольника. Какой зарядQ₄ нужно поместить в центре треугольника, чтобы указанная система зарядов находилась в равно­весии?

Решение.Все три заряда, расположенные по вер­шинам треугольника, находятся в одинаковых условиях. Поэтому достаточно выяснить, какой заряд следует по­местить в центре треугольника, чтобы какой-нибудь один из трех зарядов, напримерQi, находился в равновесии. ЗарядQi будет находиться в равновесии, если век­торная сумма действующих на него сил равна нулю (рис. 11):

F₂ + F₃ + F₄=F + F₄ = 0, (1)

где F₂, F₃, F₄ — силы, с которыми соответственно дей­ствуют на зарядQi зарядыQ₂, Q3, Qi\ F — равнодей­ствующая силF₂ иF₃.

Так как силы F иF₄ направлены по одной прямой в противоположные стороны, то векторное равенство (1) можно заменить скалярным:F —Fa =0, откудаF₄ = F. Выразив в последнем равенствеF черезF₂ и /^ и учиты­ вая, что /"з =F₂, получим ₍

Fi = F₂ V^( 1 +cos a).

Применив закон Кулона и имея в виду, что Q₂ = Q3 = =Q_lt найдем

Q,Q₄

■=^5W2(l+cosa),

4яеоП 4яе₀г

откуда

q_{4 =} -Ј^lV(2(l+cosa). (2)

77

Проверим, дает ли рас­четная формула единицу ли-

Из геометрических построений в равностороннем тре­угольнике следует, что

г/2 г

Г|

—т=, cos a = cos 60° = 1 /2.

cos (а/2) 2cos30°

С учетом этого формула (2) примет вид Q₄ = Q,/V3 .

Произведем вычисления: Q₄ = КГ⁹/УЗ Кл = 5,77-10"¹⁰ Кл = 577 пКл.

Следует отметить, что равновесие системы зарядов будет неустойчивым.

Пример 3. На тонком стержне длиной / = 20 см нахо­дится равномерно распределенный электрический заряд. На продолжении оси стержня на расстоянии а— 10 см от ближайшего конца находится точечный заряд Qi = = 40 нКл, который взаимодействует со стержнем с си­лой F = 6 мкН. Определить линейную плотность т заряда на стержне.

Решение. Сила взаимодействия F заряженного стержня с точечным зарядом Qi зависит от линейной плотности т заряда на стержне. Зная эту зависимость, можно определить т. При вычислении силы F следует иметь в виду, что заряд на стержне не является точеч­ным, поэтому закон Кулона непосредственно применить нельзя. В этом случае можно поступить следующим образом. Выделим из стержня (рис. 12) малый участок Аг с зарядом dQ = таг. Этот заряд можно рассматривать как точечный. Тогда, согласно закону Кулона,

Qixdr 7?-

dF =

4лео'

Интегрируя это выражение в пределах от а до a -f- /, получаем

Г _d^ _ Qit/ J \_\

J г² 4лео\ a a -\- l)

Qnl

F =

4лЕ₀а(а + /) '

а + I 4лео ' '²

4леоа(а + /) F

oTt

йг

Рис. 12

нейной плотности электрического заряда. Для этого в правую часть формулы вместо символов величин подста­вим их единицы:

1 Кл 1 Н-1 Кл

[а] [а + 1} [F] _ 1Ф/м-1 м-1 м-1 Н _ 1Ф-1 Н _

Кл-1 м

1 Н

1 Дж/Кл

[QUI]

гн

1 Кл/м.

1 Кл/В-1Н 1 Кл

1 В

1 Н-м

Найденная единица является единицей линейной плот­ности заряда.

Произведем вычисления:

0,1(0,1 +0,2)-6-10-9-10⁹-4-10-^в-0,2

Кл/м = 2,5-Ю-"⁹ Кл/м ж, 2,5 нКл/м.

Пример 4. Два точечных электрических заряда Qi = 1 нКл и Q₂ = —2 нКл находятся в воздухе на рас­стоянии £?=10см друг от друга. Определить напря­женность Е и потенциал ф поля, создаваемого этими зарядами в точке А, удаленной от заряда Qi на расстоя­ние г\ = 9 см и от заряда Q₂ на г₂ = 7 см.

Решение. Согласно принципу суперпозиции элек­трических полей, каждый заряд создает поле независимо от присутствия в пространстве других зарядов. Поэтому напряженность Е электрического поля в искомой точке может быть найдена как геометрическая сумма напря-женностей Ei и Е₂ полей, создаваемых каждым зарядом в отдельности: Е = Ei + E₂. Напряженности электриче­ского поля, создаваемого в воздухе (е = 1) зарядами Qi и Qi,

(1)

IQ.I

4яеоП

Е₂ =

(2)

IQ>I

4яёо'2 '

Рис. 13

Вектор Е-1 (рис. 13) направлен по силовой линии от заряда Q_lt так как этот заряд положителен; вектор Е₂ направлен также по силовой линии, но к заряду Q₂, так как этот заряд отрицателен.

78

79

(4)

Модуль вектора Е найдем по теореме косинусов:Ј=yЈ? + Јg + 2Ј,Ј₂cosa,

(3)

где а — угол между векторами Ei и Е₂, который может быть найден из треугольника со сторонамип, г₂иd:

d² — г² — г²

cosa■■

В данном случае во избежание

2пг_г

громоздких записей удобно значение cosa вычислить отдельно:

cosa:

0,238.

(0,1)² - (0.09)² - (0,07)² _

2-0,09-0,07

Подставляя выражение Е\ из (1) и £₂из (2) в (3) и вынося общий множитель 1/(4ле₀) за знак корня, полу­чаем

-л/~~^ j 1.0 !<?•!

тт.—cosa .

г\Г\

4ле,

Г2

TV -7Г^Н

В соответствии с принципом суперпозиции электриче­ских полей потенциал ф результирующего поля, созда­ваемого двумя зарядами Q\ иQ₂, равен алгебраической сумме потенциалов;

Ф=ф1+ф2- (5)

Потенциал электрического поля, создаваемого в ва­кууме точечным зарядом Q на расстоянии г от него, выра­жается формулой

Q

<р=-г*-- (⁶)

^т 4ЛЕ0Г ^v '

ф:

В нашем случае согласно формулам (5) и (6) получим

4леоГ|

или

4лЕо/'2 '

ф:

4л£о

Произведем вычисления: £ =

г, г₂) '

_-V

(Ю-⁹)² . (2-10"⁹)²

Ю^⁹-2-10

4л/(4л-9-10⁹)

(0,09)⁴ ' (0,07)⁴ ' (0,09)²-(0,07)

= 3,58-10³В/м = 3,58 кВ/м;1 / 10"⁹ , -2-10

/ 10~⁹ \ 0,09

-)в = -157В.

0,07

4л/(4л-9-10⁹)

(-0,238) В/м =

Рис. 14

Пример 5. По тон­кому кольцу равно­мерно распределен за­рядQ = 40 нКл с ли­нейной плотностью т = = 50нК.л/м. Опреде­лить напряженность Е электрического поля, создаваемого этим за­рядом в точкеА, лежа­щей на оси кольца и удаленной от его цен­тра на расстояние, рав­ное половине радиуса.

Решение.Сов­местим координатную плоскостьхОу с плоскостью коль­ца, а осьOz — с осью кольца (рис. 14). На кольце выделим малый участок длинойd/. Так как зарядdQ = xd/, находящийся на этом участке, можно считать точечным, то напряженностьdE электрического поля, создаваемого этим зарядом, может быть записана в виде

xd/ г

dE =

4ле₀'

где г — радиус-вектор, направленный от элемента d/ к точкеА.

Разложим вектор dE на две составляющие:dEi, пер­пендикулярно плоскости кольца (сонаправленную с осьюOz), иdE2, параллельную плоскости кольца (плос­костихОу), т. е.

dE=dE, + dE₂.

Напряженность Е электрического поля в точке А найдем интегрированием".

Me.+Se₂,

где интегрирование ведется по всем элементам заряженно­го кольца. Заметим, что для каждой пары зарядов dQ иdQ'(dQ= dQ'), расположенных симметрично относительно центра кольца, векторыdE₂ иdE₂ в точкеА равны по модулю и противоположны по направлению:dE₂=—dE₂.

Поэтому векторная сумма (интеграл) \dE₂=0. Состав-

L

ляющие dEi для всех элементов кольца сонаправлены

80

4—105

81

с осьюOz (единичным вектором к), т.е.dE, = kdЈ"j. Тогда

xdl

kjdfb

Так как &Е-

4леоГ²

:(/?/2)/r=l/V5, то

4т

xdf

, r = Vtf²+(/?/2)² = ^5R/2 иcosa=

dЈi =

4яео

5/?²V5"

5-\/5яе₀Л²

d/ = -

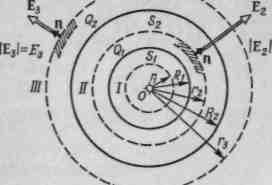
областях (рис. 15): обла­сти I(ri<Ri), области // (/?1</-2</?г), области /// (г₃>Я₂).

1. Для определения на­пряженности Е\- в области / проведем гауссову повер­хностьSi радиусомГ\ и воспользуемся теоремой Остроградского—Гаусса:

2т

Е=к$

то¹/

Таким образом,

2лЯ

-=k-

5У5е₀Я

о 5-^5keoR²

2т2лт

4ят

Из соотношения Q = 2nRx определим радиус кольца:/?=Q/(2nt). Тогда

Е = к

5~\J5eoQ

5V5eoQ Модуль напряженности

4лт²

5-\/5eoQ

Проверим, дает ли правая часть полученного равен­ства единицу напряженности (В/м):

1 Кл 1 Ф-1 м

1 В/м.

[т²] (1 Кл/м)²

[eolIQ]

1 Ф/м • 1 Кл

Выразим физические величины, входящие в форму­лу (1), в единицах СИ (т=5-10~⁸Кл/м, <Э=4.кНКл, ео=8,85- Ю^-12Ф/м) и произведем вычисления:

■В/м = 7,92 кВ/м.

4-3,14-(5-10"⁸)²

&V5-8,85-l(r¹²-4-l(r

Пример 6. Две концентрические проводящие сферы радиусами/?i = 6cm и /?₂= 10 см несут соответственно заряды (?1 = 1нКл иQ₂=—- 0,5 нКл. Найти напряжен­ностьЕ поля в точках, отстоящих от центра сфер на рас­стояниях /-1 = 5 см, г₂= 9 см,г₃= 15 см. Построить графикЕ(г).

Решение.Заметим, что точки, в которых требуется найти напряженности электрического поля, лежат в трех

!,

Рис. 15

Ј„dS = 0

(так как суммарный заряд, находящийся внутри гауссо­вой поверхности, равен нулю). Из соображений симметрии

Е_п=Е\ = const. Следовательно,Јi® dS = 0 и £| (напря­женность поля в области /) во всех точках, удовлетворяю­щих условиюri<.Ri, будет равна нулю.

2. В области // гауссову поверхность проведем радиу­сом г₂. В этом случае*

\ E_ndS=Qi/e₀,

(так как внутри гауссовой поверхности находится только заряд Qi).

Так как Е_п = Е = const, тоЕ можно вынести за знак интеграла:

е\ dS = Qi/e₀, илиES₂=Qi/zo.

Обозначив напряженность Е для области // черезЕг, получим

Ј₂=Qi/(eoS₂), гдеS₂ = 4nr₂ — площадь гауссовой поверхности. Тогда

(1)

4яёо7Г'

3. В области /// гауссова поверхность проводится ра­диусом гз. Обозначим напряженность Е области /// через

* Диэлектрическую проницаемость е среды будем считать равной единице (вакуум).

82

4*

83

Е₃ и учтем, что в этом случае гауссова поверхность охва­тывает обе сферы и, следовательно, суммарный заряд бу­дет равен Qi + Q₂. Тогда

Р _ Ql + <?2

4ле₀Гз

Заметив, что Q₂<0, это выражение можно переписать в виде

_Е Q.-IQ_ai ₍₂₎

4леоЛз ^v

Убедимся в том, что правая часть равенств (1) и (2) дает единицу напряженности:

1 Кл 1 Ф-1 м

[ Q] 1 Кл

1 Ф/м-1 м²

= 1 В/м.

Выразим все величины в единицах СИ (Qi=10 ⁹ Кл, Q₂= — 0,5-1 СГ⁹Кл, /-, = 0,09 м, /-2 = 0,15 м, 1/(4ле₀) = = 9-10⁹м/Ф) и произведем вычисления:

£2 = 9-10⁹^_тВ/м=1,11 кВ/м;

-В/м = 200 В/м.

(0,09)' £₃ = 9.10⁹⁽¹-°'^5)1(Г

(0,15)^г

Построим график Е(г). В области I(n<.R\) E = 0. В области // (#1<><с/?2) Е₂ {г) изменяется по закону 1/г². В точке r = R\ напряженность Ј"2(/?i) = Q1 /(4эте₀/?1) = = 2,5кВ/м. В точке r=R₂ (r стремится к R₂ слева) £₂(7?₂) = Q_l/(Ane₀Rl) = 0,9 кВ/м. В области /// {r>R₂) Е₃{г) изменяется по закону 1/л², причем в точке r=R₂ (г стре­мится к R₂ справа) E₃(R₂) = {Q\ — |Q2l/(4ne₀/?l) = = 0,45 кВ/м. Таким образом, функция Е(г) в точках

Е,кВ/м ^п

г = R\ и г = R₂ терпит раз­рыв.

2.50

0,90

0,45

Рис. 16

График зависимостиЕ_г представлен на рис. 16. Пример 7. Точечный заряд Q = 25 нКл нахо­дится в поле, созданном прямым бесконечным ци­линдром радиусом R = = 1 см, равномерно заря­женным с поверхностной плотностью о=0,2 нКл/см².

Определить силу F,. действующую на заряд, если его рас­стояние от оси цилиндра г== 10 см.

Решение. Значение силы F, действующей на то­чечный заряд Q, находящийся в поле, определяется по формуле

F=QE, (1)

где Е — напряженность поля.

Как известно, напряженность поля бесконечно длин­ного равномерно заряженного цилиндра

где т — линейная плотность заряда.

Выразим линейную плотность т через поверхностную плотность о. Для этого выделим элемент цилиндра дли­ной / и выразим находящийся на нем заряд Q двумя способами: Q=oS = a2nRl, Q = xl. Приравняв правые части этих формул и сократив полученное равенство на /, найдем т = 2л/?0. С учетом этого формула (2) примет вид Е— Ro/(Eor). Подставив выражение £ в (1), получим

_F=r QeR Произведем вычисления:

F = ^2,5₈'^"io-._г'⁰к)⁶' * Н = 5,65 • 10,-⁴ Н=565 мкН.

Сила F сонаправлена с напряженностью Е, которая в силу симметрии (цилиндр бесконечно длинный) пер­пендикулярна поверхности цилиндра.

Пример 8. По тонкой нити, изогнутой по дуге окруж­ности, равномерно распределен заряд с линейной плот­ностью т=10нКл/м. Определить напряженность Е и потенциал ф электрического поля, создаваемого таким распределенным зарядом в точке, совпадающей с цент­ром кривизны дуги. Длина / нити составляет '/з длины окружности и равна 15 см.

Решение. Выберем оси координат так, чтобы на­чало координат совпадало с центром кривизны дуги, а ось Оу была бы симметрично расположена относительно концов дуги (рис. 17). На нити выделим элемент длины d/. Заряд dQ = rd/, находящийся на выделенном участке, можно считать точечным.

84

85

315. Бесконечный тонкий стержень, ограниченный с одной стороны, несет равномерно распределенный заряд с линейной плотностью т = 0,5 мкКл/м. Определить на­ пряженность Е электрического поля, создаваемого рас­ пределенным зарядом в точкеА, лежащей на оси стерж­ ня на расстоянии а = 20 см от его начала.

316. По тонкому кольцу радиусом /? = 20см равно­мерно распределен с линейной плотностью т = 0,2 мкКл/м заряд. Определить напряженность Е электрического по­ля, создаваемого распределенным зарядом в точке А, находящейся на оси кольца на расстоянииh = 2R от его центра.

317. По тонкому полукольцу равномерно распределен заряд Q = 20 мкКл с линейной плотностью т=0,1 мкКл/м. Определить напряженность Е электрического поля, со­здаваемого распределенным зарядом в точкеО, совпа­дающей с центром кольца.

318. Четверть тонкого кольца радиусом R=10 см несет равномерно распределенный зарядQ = 0,05mkKji. Определить напряженность Е электрического поля, со­здаваемого распределенным зарядом в точке О, совпа­дающей с центром кольца.

319. По тонкому кольцу равномерно распределен заряд Q= 10 нКл с линейной плотностью т=0,01 мкКл/м. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точкеА, лежа­щей на оси кольца и удаленной от его центра на расстоя­ние, равное радиусу кольца.

320. Две трети тонкого кольца радиусом Я=\0см несут равномерно распределенный с линейной плотностью т=0,2 мкКл/м заряд. Определить напряженность Е элек­трического поля, создаваемого распределенным зарядом в точкеО, совпадающей с центром кольца.

321. На двух концентрических сферах радиусом R и2R равномерно распределены заряды с поверхностными плотностями а, и а₂(рис. 24). Требуется: 1) используя теорему Остроградского—Гаусса, найти зависимостьЕ(г) напряженности электрического поля от расстояния для трех областей: /, // и ///. Принятьoi = 4o, 02 = 0; 2) вы­числить напряженностьЕ в точке, удаленной от центра на расстояниег, и указать направление вектора Е. Принятьа = 30 нКл/м²,r = l,5R; 3) построить графикЕ(_Г).

322. См. условие задачи 321. В п. 1 принять а,==а, 02=—о. В п. 2 принять (т = 0,1 мкКл/м², г=3.

100

323. См. условие задачи 321. В п. 1 принять 0i =—4а, 02 = ст. В п. 2 принять ст = 50 нКл/м²,r—l,5R.

324. См. условие задачи 321. В п. 1 принять а\ = —2ст, 02 = а. В п. 2 принять а = 0,1 мкКл/м²,r=3/?.

325. На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями 0i и 0₂(рис. 25). Требуется: 1) используя теорему Остроградского—Гаусса и принцип суперпози­ции электрических полей, найти выражениеЕ{х) напря­женности электрического поля в трех областях: /, // и ///. Принять0i = 20, 02 = о; 2) вычислить напряженностьЕ поля в точке, расположенной слева от плоскостей, и ука­зать направление вектора Е; 3) построить графикЕ(х).

///

Рис. 24

Рис. 25

326. См. условие задачи 325. В п. 1 принять 0i = = —4о, 02=20. В п. 2 принять о=40 нКл/м²и точку расположить между плоскостями.

327. См. условие задачи 325. В п. 1 принять 0i = o, 02= —2о. В п. 2 принять 0 = 20 нКл/м²и точку располо­жить справа от плоскостей.

Рис. 26

101

328. На двух коак­ сиальных бесконечных цилиндрах радиусамиR и2R равномерно распре­ делены заряды с поверх­ностными ПЛОТНОСТЯМИ 01 и 0₂(рис. 26). Требуется: 1) используя теорему Остро градского—Гаусса: найти зависимостьЕ(г) напряженности электри­ ческого поля от расстоя­ ния для трех областей:

/, // и ///. Принять о\ = — 2о, о₂ = а; 2) вычислить напря­женность Е в точке, удаленной от оси цилиндров на рас­стояние г, и указать направление вектора Е. Принять а = 50 нКл/м², г — 1,5/?; 3) построить график Е(г).

2_Г

I I

329. См. условие задачи 328. В п. 1 принять o"i = a, 02=—а. В п. 2 принять 0 = 60 нКл/м², r=3R.

330. См. условие задачи 328. В п. 1 принять 0i = —0, or₂=4o. В п. 2 принять 0 = 30 нКл/м², /- = 4/?.

331. Два точечных заряда Qi = 6 нКл и Q₂ = 3 нКл находятся на расстоянии d = 60 см друг от друга. Какую работу необходимо совершить внешним силам, чтобы уменьшить расстояние между зарядами вдвое?

332. Электрическое поле создано заряженным прово­дящим шаром, потенциал ф которого 300 В. Определить работу сил поля по перемещению заряда <3 = 0,2мкКл из точки / в точку 2 (рис. 27).

р	—,	1 ?—		2 — -о
—'	Ш* 1		2R
				*

_I

2а

Рис. 27

Рис. 28

333. Электрическое поле создано зарядами Q\ = = 2 мкКл и Q₂ =—2 мкКл, находящимися на расстоянии а= 10 см друг от друга. Определить работу сил поля, совершаемую при перемещении заряда (? = 0,5мкКл из точки 1 в точку 2 (рис. 28).

334. Две параллельные заряженные плоскости, по­верхностные плотности заряда которых о\ = 2 мкКл/м² и 0₂ = —0,8 мкКл/м², находятся на расстоянии d = = 0,6 см друг от друга. Определить разность потенциа­лов U между плоскостями. _ч

335. Диполь с электрическим моментом р = 100 пКл- м свободно установился в свободном электрическом поле напряженностью Е = 200 кВ/м. Определить работу внешних сил, которую необходимо совершить для поворо­та диполя на угол а= 180°.

102

336. Четыре одинаковых капли ртути, заряженных до потенциала ф= 10 В, сливаются в одну. Каков потен­циал ф1 образовавшейся капли?

337. Тонкий стержень согнут в кольцо радиусом R = = 10 см. Он равномерно заряжен с линейной плотностью заряда т = 800 нКл/м. Определить потенциал ф в точке, расположенной на оси кольца на расстоянии h = 10 см от его центра.

338. Поле образовано точечным диполем с электри­ческим моментом р = 200 пКл • м. Опредить разность потенциалов U двух точек поля, расположенных симмет­рично относительно диполя на его оси на расстоянии г = = 40 см от центра диполя.

339. Электрическое поле образовано бесконечно длин­ной заряженной нитью, линейная плотность заряда кото­рой т"= 20 пКл/м. Определить разность потенциалов U двух точек поля, отстоящих от нити на расстоянии г\ = 8 см и г% = 12 см.

340. Тонкая квадратная рамка равномерно заряжена с линейной плотностью заряда т = 200 пКл/м. Опреде­лить потенциал ф поля в точке пересечения диагоналей.

341. Пылинка массой т = 200 мкг, несущая на себе заряд Q = 40 нКл, влетела в электрическое поле в на­правлении силовых линий. После прохождения разности потенциалов U = 200 В пылинка имела скорость v = = 10 м/с. Определить скорость vo пылинки до того, как она влетела в поле.

342. Электрон, обладавший кинетической энергией Т = 10 эВ, влетел в однородное электрическое поле в направлении силовых линий поля. Какой скоростью будет обладать электрон, пройдя в этом поле разность потен­циалов U = 8 В?

343. Найти отношение скоростей ионов Си⁺⁺ и К⁺, прошедших одинаковую разность потенциалов.

344. Электрон с энергией Т = 400 эВ (в бесконечнос­ти) движется вдоль силовой линии по направлению к поверхности металлической заряженной сферы радиусом R = 10 см. Определить минимальное расстояние а, на которое приблизится электрон к поверхности сферы, если заряд ее Q = — 10 нКл.

345. Электрон, пройдя в плоском конденсаторе путь от одной пластины до другой, приобрел скорость v = = 10⁵ м/с. Расстояние между пластинами d = 8 мм. Найти: 1) разность потенциалов U между пластинами; 2) поверхностную плотность заряда о на пластинах.

юз

346. Пылинка массой т — 5 нг, несущая на себе N = = 10 электронов, прошла в вакууме ускоряющую раз­ность потенциалов U = 1 MB. Какова кинетическая энер­гия Т пылинки? Какую скорость v приобрела пылинка?

347. Какой минимальной скоростью v_min должен обла­дать протон, чтобы он мог достигнуть поверхности заря­женного до потенциала ср = 400 В металлического шара (рис. 29)?

348. В однородное электрическое поле напряжен­ностью Е = 200 В/м влетает (вдоль силовой линии) электрон со скоростью v₀ = 2 Мм/с. Определить расстоя­ние /, которое пройдет электрон до точки, в которой его скорость будет равна половине начальной.

349. Электрическое поле создано бесконечной заря­женной прямой линией с равномерно распределенным зарядом (т = 10 нКл/м). Определить кинетическую энер­гию Т₂ электрона в точке 2, если в точке / его кинетиче­ская энергия Т_х = 200 эВ (рис. 30).

г
—л	2		1 —-о
< " >		2а

Рис. 29

Рис. 30

350. Электрон движется вдоль силовой линии одно­родного электрического поля. В некоторой точке поля с потенциалом ф] = 100 В электрон имел скорость V\ = = 6 Мм/с. Определить потенциал ф₂ точки поля, дойдя до которой электрон потеряет половину своей скорости.

351. Конденсаторы емкостью С\ = Ъ мкФ и Сг = = 10 мкФ заряжены до напряжений U\ = 60 В и U₂ = = 100 В соответственно. Определить напряжение на об­кладках конденсаторов после их соединения обкладками, имеющими одноименные заряды.

352. Конденсатор емкостью С\ = 10 мкФ заряжен до напряжения U = 10 В. Определить заряд на обкладках этого конденсатора после того, как параллельно ему был

подключен другой, незаряженный, конденсатор ем­костью С₂ = 20 мкФ.

353. Конденсаторы емкостями G = 2 мкФ, С₂ = = 5 мкФ и С₃= 10 мкФ соединены последовательно и находятся под напряжением U = 850 В. Определить на­пряжение и заряд на каждом из конденсаторов.

354. Два конденсатора емкостями С\ = 2 мкФ и С₂ = = 5 мкФ заряжены до напряжений U\ = 100 В и U₂ = = 150 В соответственно. Определить напряжение на об­кладках конденсаторов после их соединения обкладками, имеющими разноименные заряды.

355. Два одинаковых плоских воздушных конденсато­ра емкостью С = 100 пФ каждый соединены в батарею последовательно. Определить, на сколько -изменится емкость С батареи, если пространство между пластинами одного из конденсаторов заполнить парафином.

356. Два конденсатора емкостями С\ = 5 мкФ и С₂ = = 8 мкФ соединены последовательно и присоединены к батарее с ЭДС ё = 80 В. Определить заряды Qi и Q₂ конденсаторов и разности потенциалов U\ и U₂ между их обкладками.

357. Плоский конденсатор состоит из двух круглых пластин радиусом R = 10 см каждая. Расстояние между пластинами d = 2 мм. Конденсатор присоединен к источ­нику напряжения U = 80 В. Определить заряд Q и на­пряженность Е поля конденсатора в двух случаях: а) диэлектрик — воздух; б) диэлектрик — стекло.

358. Два металлических шарика радиусами R\ — = 5 см и R₂ = 10 см имеют заряды Qi = 40 нКл и Q₂ = = —20 нКл соответственно. Найти энергию W, которая выделится при разряде, если шары соединить проводни­ком.

359. Пространство между пластинами плоского кон­денсатора заполнено двумя слоями диэлектрика: стекла толщиной d\ = 0,2 см и слоем парафина толщиной d₂ = = 0,3 см. Разность потенциалов между обкладками U = =.300 В. Определить напряженность Е поля и падение потенциала в каждом из слоев.

360. Плоский конденсатор с площадью пластин S = = 200 см² каждая заряжен до разности потенциалов U = = 2 кВ. Расстояние между пластинами d=2 см. Диэлект­рик — стекло. Определить энергию W поля конденсатора и плотность энергии w поля.

1. Катушка и амперметр соединены последователь­но и подключены к источнику тока. К клеммам катушки

360. 104

105

магнитная индукция В в точке А определяется интегри^

^{рованием:}

_{Э = 5 dB,}

_i

где интегрирование ведется по всем элементам d/ кольца. Разложим вектор dB на две составляющие: dB_L> перпендикулярную плоскости кольца, и dBy, параллель ную плоскости кольца, т. е.

_{dB = dB_L + dB|].}

После сокращения на 2л и замены cos p на R/r (рис. 35) получим

_\iolR²

.3

_В

_2/

Проверим, дает ли правая часть равенства единицу магнитной индукции (Тл):

МИ!#²] 1Гн-1А.1м² 1Гн-\А² 1 Дж

[г³] м-1м³ 1А-1м² 1А-1м²

_{1 Н-1 м}

_{i Тл.}

_{1 А-1 м}

Здесь мы воспользовались определяющей формулой для магнитной индукции:

_»ах

_В

м_и

_Тогда

_{1 ~ 1 Н* 1 м}

_{1 ТЛ = : л : ц}

_{1 А-1 м}

_{Рис. 35}

_Тогда

^{В = 5 dBx + J dB}

^{Заметив, что \ dBn = 0 из соображений симметрии и что}

векторы dB_L от различных элементов d/ сонаправлены, заменим векторное суммирование (интегрирование) скалярным:

_В

^JdBx,

_{где dB}

,_x==dBcosP и dB = -p—_г (поскольку dl перпен­дикулярен г и, следовательно, sina—1). Таким образом*

_2яК

с

_В

_{г со}

_{4я г}

\ioI cos p • 2nR 4n?

₁₁₆

Выразим все величины в единицах СИ и произведем вычисления:

4я-10-⁷.80.(0,1)² _Тл==628.Ю-⁵ ТЛ,

2-(0,2)^J

или В = 62,8 мкТл.

Вектор В направлен по оси кольца (пунктирная стрел­ка на рис. 35) в соответствии с правилом буравчика.

Пример 4. Длинный провод с током / = 50 А изогнут под углом ос=2я/3. Определить магнитную индукцию В в точке А (рис. 36). Расстояние d=5 см.

Решение. Изогнутый провод можно рассматри­вать как два длинных провода, концы которых соединены в точке О (рис. 37). В соответствии с принципом супер­позиции магнитных полей магнитная индукция В в точ­ке А будет равна геометрической сумме магнитных ин­дукций Bi и Вг полей, создаваемых отрезками длинных проводов / и 2, т.е. B=Bi-f-B2. Магнитная индукция Вг Равна нулю. Это следует из закона Био—Савара—Лап­ласа, согласно которому в точках, лежащих на оси привода, dB = 0 ([ dlr] = 0).

₁₁₇