
- •Вопросы к экзамену по физике (пгс) I часть
- •15. Удар абсолютно упругих и неупругих тел.
- •21. Постулаты специальной теории относительности.
- •28. Давление газа с точки зрения молекулярно-кинетической теории. Уравнение состояния идеального газа.
- •34. Средняя кинетическая энергия молекул. Молекулярно-кинетическое толкование абсолютной температуры.
- •Внутренняя энергия
- •35. Работа газа. Количество теплоты 37. Теплоемкость.
- •30. Закон Максвелла для распределения молекул идеального газа по скоростям и энергиям их теплового движения. Средние скорости теплового движения частиц.
- •33. Число степеней свободы. Закон равномерного распределения энергии по степеням свободы.
- •29. Барометрическая формула. Распределение Больцмана.
- •31. Принцип детального равновесия. Среднее число столкновений и средняя длина свободного пробега молекул. Вакуум.
- •32. Молекулярно-кинетическая теория явлений переноса в неравновесной системе.
- •35. Работа газа при изменении его объема. Внутренняя энергия термодинамической системы.
- •36. Количество теплоты. Первое начало термодинамики. Применение первого начала к изопроцессам.
- •37. Теплоемкость. Удельная и молярная теплоемкости. Зависимость теплоемкости идеального газа от вида процесса. Недостаточность классической теории теплоемкости.
- •40. Термодинамическая вероятность. Определение энтропии неравновесной системы через термодинамическую вероятность состояния.
- •41. Силы и потенциальная энергия межмолекулярного взаимодействия. Эффективный диаметр молекул.
- •42. Уравнение Ван-дер-Ваальса. Изотермы Ван-дер-Ваальса и их анализ.
- •42. Метастабильные состояния. Критическая точка.
- •43. Внутренняя энергия реальных газов.
- •44. Понятие фазы, фазового равновесия и превращения. Правило фаз Гиббса.
21. Постулаты специальной теории относительности.

21. Преобразования Лоренца. 22. Относительность длин и промежутков времени. 23.Релятивистский закон сложения скоростей.




24. Релятивистский импульс. Основной закон релятивистской динамики материальной точки.

24. Взаимосвязь массы и энергии.
25. Соотношение между полной энергией и импульсом частицы.
26. Релятивистское выражение для кинетической энергии.

27. Неинерциальные системы отсчета. Силы инерции
Как
известно, законы Ньютона выполняются
только в инерциальных системах отсчета.
Системы отсчета, которые движутся
относительно инерциальной системы с
ускорением, называются неинерциальными.
В неинерциальных системах законы
Ньютона, вообще говоря, уже применять
нельзя. Однако законы динамики можно
применять и для них, если кроме сил,
которые обусловленны воздействием тел
друг на друга, ввести в рассмотрение
понятие силы особого рода - так
называемую силу
инерции.
При
учете сил инерции второй закон Ньютона
будет справедлив для любой системы
отсчета: произведение массы тела на
ускорение в рассматриваемой системе
отсчета равно сумме всех сил, действующих
на данное тело (учитывая и силы инерции).
При этом силы инерции Fin должны
быть такими, чтобы вместе с силами F,
обусловленными воздействием тел друг
на друга, они сообщали телу ускорение а',
каким оно обладает в неинерциальных
системах отсчета, т. е.
![]() (1)
Так
как F=ma (a -
ускорение тела в инерциальной системе
отсчета), то
(1)
Так
как F=ma (a -
ускорение тела в инерциальной системе
отсчета), то
![]() Силы
инерции обусловлены ускоренным движением
системы отсчета относительно измеряемой
системы, поэтому в общем случае следует
учитывать следующие случаи возниконовения
этих сил: 1) силы инерции при ускоренном
поступательном движении системы отсчета;
2) силы инерции, которые действуют на
тело, покоящееся во вращающейся системе
отсчета; 3) силы инерции, которые действуют
на тело, движущееся во вращающейся
системе отсчета.
Силы
инерции обусловлены ускоренным движением
системы отсчета относительно измеряемой
системы, поэтому в общем случае следует
учитывать следующие случаи возниконовения
этих сил: 1) силы инерции при ускоренном
поступательном движении системы отсчета;
2) силы инерции, которые действуют на
тело, покоящееся во вращающейся системе
отсчета; 3) силы инерции, которые действуют
на тело, движущееся во вращающейся
системе отсчета.
28. Давление газа с точки зрения молекулярно-кинетической теории. Уравнение состояния идеального газа.
Давление газа на стенку сосуда есть результат ударов малекул газа об эту стенку. При каждом ударе молекула газа действует на стенку с определенной (с макроскопической точки зрения бесконечно малой) силой. Обратно направленная сила, с которой действует на молекулу стенка сосуда, заставляет молекулу отражаться от стенки. Если бы в сосуде содержалось всего несколько молекул, гопх удары следовали бы друг за другом редко и беспорядочно, п нельзя было бы говорить ни о какой регулярной силе давления, действующей на стенку. Мы имели бы дело с отдельными практически мгновенными бесконечно малыми толчками, которым время от времени подвергалась бы стенка. Если же число молекул в сосуде очень велико, то будет велико и числе ударов их о стенку сосуда. Удары станут следовать непрерывно друг за другом. Одновременно о стенку сосуда будет ударяться громадное количество молекул. Бесконечно малые силы отдельных ударов складываются в конечную и почти постоянную силу, действующую на стенку. Эта сила, усредненная по времени, и есть давление газа, с которым имеет дело макроскопическая физика.
Уравнение состоянияидеального газа (иногда уравнение Клапейрона или уравнение Менделеева—Клапейрона) — формула, устанавливающая зависимость между давлением,молярным объёмомиабсолютной температуройидеального газа. Уравнение имеет вид:
![]()
где
 — давление,
— давление, — молярный
объём,
— молярный
объём, — универсальная
газовая постоянная
— универсальная
газовая постоянная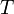 — абсолютная
температура,К.
— абсолютная
температура,К.
Так
как ![]() ,
где
,
где![]() —количество
вещества, а
—количество
вещества, а![]() ,
где
,
где![]() —
масса,
—
масса,![]() —молярная
масса, уравнение состояния можно
записать:
—молярная
масса, уравнение состояния можно
записать:
![]()
Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.
В случае постоянной массы газа уравнение можно записать в виде:
![]()
![]()
Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:

