
- •Введение
- •Т е м а 1. Изучение направления, формы и силы связи между признаками
- •Т е м а 2. Вычисление коэффициента корРеляции
- •Корреляции между показателями плодовитости свиноматок (гол.) белорусской мясной породы и показателями плодовитости их дочерей по третьему опоросу
- •Т е м а 3. Вычисление коэффициента корРеляции
- •Тела овец (х, кг) и настрига шерсти (у, кг)
- •Массой овец и настригом шерсти
- •Т е м а 4. Изучение криволинейного типа связи и вычисление корреляционного отношения
- •Контрольные вопросы
- •Приложения
- •Длина и вес самок лосося разных возрастных групп
Т е м а 4. Изучение криволинейного типа связи и вычисление корреляционного отношения
Цель занятия. Изучить криволинейный тип связи. Научиться определять силу криволинейной связи при помощи корреляционного отношения.
Содержание и методика. Кроме прямолинейных и близких к ним связей, для определения которых можно применять коэффициент корреляции (r), существует многообразие связей криволинейного типа. С целью их установления используют другие формулы и коэффициенты. Многие признаки рыб проявляют криволинейную связь с возрастом. Изменение живой массы рыбы от рождения до наступления половой зрелости выражается так называемой логистической кривой. У насекомых наблюдаются периодические вспышки усиления и затухания в размножении, что можно выразить периодической синусоидной кривой.
При наличии криволинейного типа связи между признаками, как правило, используют показатель корреляционного соотношения η, который позволяет определить величину связи, но не выявляет ее направления, т. е. этот коэффициент всегда положительный. Его величина изменяется от 0 до +1. Корреляционное соотношение можно применять для измерения как криволинейных, так и прямолинейных связей.
При криволинейном типе связи величина η всегда будет больше величины r, вычисленной на том же материале. Если же связь прямолинейна, то η = r. Корреляционное соотношение имеет два значения: у по х и х по у, следовательно, оно выявляет неравенство связей, так как ηху ≠ ηух.
В общем виде формула корреляционного соотношения включает показатели групповых (частных) средних квадратических и общих средних квадратических отклонений:
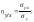 (20)
(20)
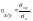 (21)
(21)
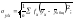 (22)
(22)
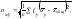 (23)
(23)
Для вычисления корреляционного соотношения по вариационным рядам, оформленным с распределением признаков на варьирующие классы (т. е. при взвешенных рядах), воспользуемся формулой
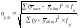 (24)
(24)
где
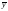 общ
– среднее арифметическое признака у;
общ
– среднее арифметическое признака у;
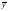
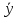 част
– средние величины признака у
по классам признака х.
Здесь
част
– средние величины признака у
по классам признака х.
Здесь
зависимой функцией является признак у, а независимым
аргументом – признак х.
Для определения ŋух составляют корреляционную решетку и определяют эмпирические величины регрессии признака у в зависимости от признака х.
П р и м е р. Определить влияние возраста (х) самок лахвинского карпа на их рабочую плодовитость (у) (тыс. шт.). Возраст выражен продолжительностью использования самок (лет) с момента наступления половой зрелости. В выборку вошло 70 нерестов (n > 30), полученных от 50 самок карпа, и учтена рабочая плодовитость для каждого нереста.
1. Составляем корреляционную таблицу зависимости у-признака от х-признака (табл. 5).
2. Вычисляем
эмпирические величины регрессии
изменения признака рабочей плодовитости
(у)
от изменения возраста (х)
–
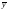 част.
Для этого умножаем частоты клеток
решетки (fух)
на соответствующую величину признака
у каждого класса, т. е. по столбцам, и для
каждого столбца записываем получаемую
сумму от умножения fух
.
у
и делим на число fхi:
част.
Для этого умножаем частоты клеток
решетки (fух)
на соответствующую величину признака
у каждого класса, т. е. по столбцам, и для
каждого столбца записываем получаемую
сумму от умножения fух
.
у
и делим на число fхi:
1-й столбец: (6·80+4·110):(6+4)= (480+440):10=920:10=92;
2-й столбец: (3·80+6·110+1·140):10=104 и т. д.
Полученный ряд изменений у по х демонстрирует эмпирический ряд регрессии, из которого видно, что с 3-го нереста по 6-й наблюдается повышение рабочей плодовитости самок, а с 7-го – снижение.
Т а б л и ц а 5. Корреляционная решетка
|
у–рабочая плодовитость, тыс. шт. |
х–возраст (по продолжительности использования), лет |
fу |
у×fу |
(y
–
| |||||||||||
|
Границы |
Середина класса, у |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
| |||
|
70 – 90 |
80 |
6 |
3 |
2 |
|
|
|
1 |
1 |
13 |
1040 |
(80 –115,6)2× ×13= 16475,7 | |||
|
100 – 120 |
110 |
4 |
6 |
6 |
5 |
6 |
2 |
2 |
3 |
34 |
3740 |
1066,2 | |||
|
130 – 150 |
140 |
|
1 |
5 |
4 |
4 |
4 |
1 |
1 |
20 |
2800 |
11907,2 | |||
|
160 – 180 |
170 |
|
|
2 |
1 |
|
|
|
|
3 |
510 |
8878,1 | |||
|
fх |
10 |
10 |
15 |
10 |
10 |
6 |
4 |
5 |
fу =70 |
у×fу= = 8090 |
(y– | ||||
|
|
92 |
104 |
124 |
128 |
122 |
130 |
110 |
110 | |||||||
|
( |
5569,6 |
1345,6 |
1058,4 |
1537,6 |
409,6 |
1244,2 |
125,44 |
156,8 |
( | ||||||
3. Определяем
среднюю рабочую плодовитость самок по
всем возрастным группам, т. е.
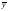
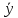 общ.
Для этого перемножаем частоты ряда у
(fу)
по каждому классу на середину класса.
Суммируем данные по всем четырем классам
признака плодовитости и, деля сумму на
общее число обследованных нерестов
(n=70),
получаем среднюю плодовитость по всему
корреляционному комплексу. Эти данные
введены в табл. 5 (колонка «у×fу»).
Отсюда средняя рабочая плодовитость
составит:
общ.
Для этого перемножаем частоты ряда у
(fу)
по каждому классу на середину класса.
Суммируем данные по всем четырем классам
признака плодовитости и, деля сумму на
общее число обследованных нерестов
(n=70),
получаем среднюю плодовитость по всему
корреляционному комплексу. Эти данные
введены в табл. 5 (колонка «у×fу»).
Отсюда средняя рабочая плодовитость
составит:
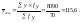 (25)
(25)
4. Далее обработка
данных сопровождается получением суммы
квадратов отклонения для показателей
у
от общей средней и умножения на частоты
ряда у,
т. е. (y
–
 общ)2×fу
(последний столбец табл. 5).
общ)2×fу
(последний столбец табл. 5).
5. Затем производим
вычисление суммы квадратов отклонений
частных средних (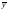 част)
от общей средней, умноженных на частоты
для эмпирического ряда регрессии, т. е.
на fх,
в соответствии с выражением
(
част)
от общей средней, умноженных на частоты
для эмпирического ряда регрессии, т. е.
на fх,
в соответствии с выражением
(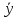
 част–
част–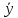
 общ)2×fх.
Этот расчет приведен в последней строчке
таблицы.
общ)2×fх.
Этот расчет приведен в последней строчке
таблицы.
6. Полученные величины вводим в формулу (24) корреляционного соотношения при обработке взвешенных рядов:

Полученная величина ηух указывает на большую зависимость рабочей плодовитости самок лахвинского карпа от их возрастного показателя, что следует из ряда регрессии у по х.

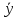
 общ)2×fу
общ)2×fу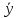
 общ)2×fу
= =
38327,2
общ)2×fу
= =
38327,2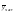
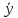 тыс. шт.
тыс. шт.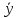
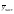 –
–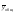 )2×fх
)2×fх част
–
част
–
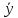
 общ)2×fх
=11447,2
общ)2×fх
=11447,2