Задачи контрольной работы

В задачах 121–140 найти неопределенные интегралы и результат интегрирования проверить дифференцированием.

121. .	122. .
123. .	124. .
125. .	126. .
127. .	128. .
129. .	130. .
131. .	132. .
133. .	134. .
135. .	136. .
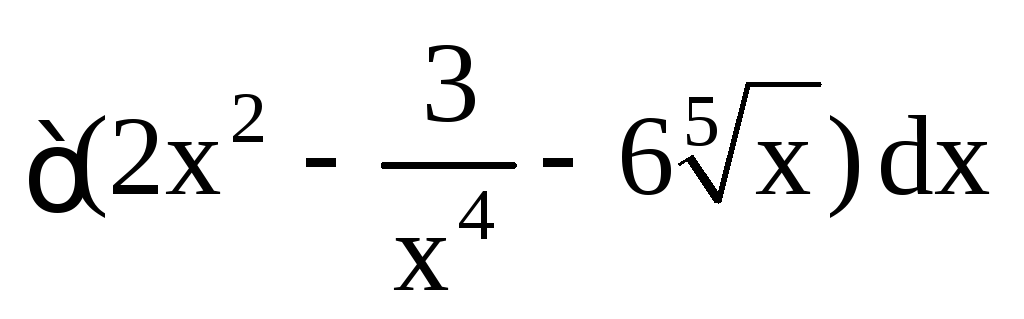137. .	138. .
139. .	140. .

Решение типового примера

Найти и результат проверить дифференциро-ванием.

Р е ш е н и е.

Преобразуем подынтегральную функцию к виду, удобному для интегрирования. Для этого применим следующие формулы:

,,

.

П р о в е р к а.

.

Получена подынтегральная функция.

В задачах 141–160 найти неопределённые интегралы методом под­становки (замены переменной).

141. 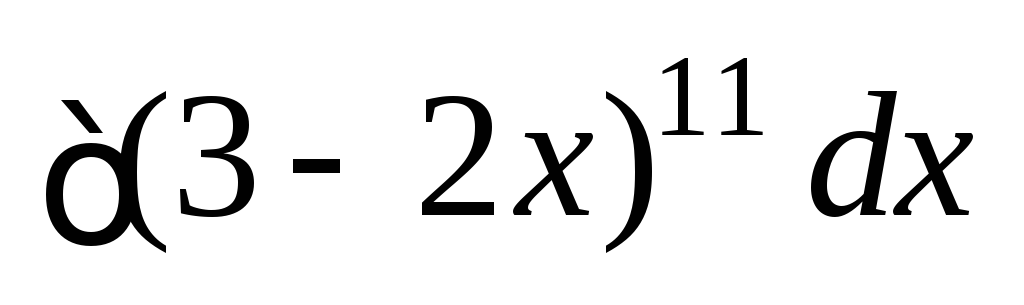.	142. .
143. .	144. .
145. .	146. .
147. .	148. .
149. .	150. .
151. .	152. .
153. .	154. .
155. .	156. .
157. .	158. .
159. 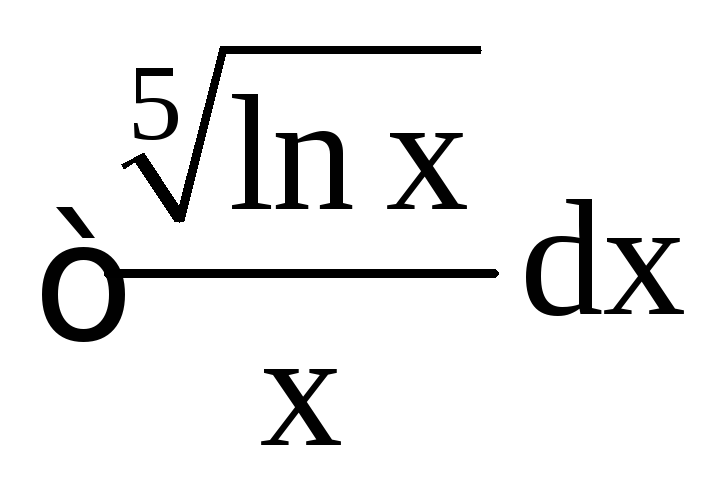.	160. .

Решение типового примера

Найти неопределённый интеграл .

Р е ш е н и е.

Применим подстановку , тогда.

Получим .

В задачах 161–180 найти неопределённые интегралы методом

интегрирования по частям.

161. .	162. .	163. .
164. .	165. .	166. .
167. .	168. .	169. .
170. .	171. .	172. .
173. .	174. .	175. .
176. .	177. .	178. .
179. .	180. .

Решение типового примера

1. Найти .

Р е ш е н и е.

Применим формулу интегрирования по частям:

.

.

2. Найти .

Р е ш е н и е.

==

=.

В задачах 181 – 200вычислить площадь фигуры, ограниченной линиями.

181. .	182. .
183. .	184. .
185. .	186. .
187. .	188. .
189. .	190. .
191. .	192. .
193. .	194. .
195. .	196. .
197. .	198. .
199. .	200.

Решение типового примера

Вычислить площадь фигуры, ограниченной линиями:

Р е ш е н и е.

Найдём абсциссы точек пересечения линий:

, , .

Сделаем чертеж (рис. 3).

Рис. 3.

Вычислим площадь по формуле

где– линии, ограничивающие фигуру, причёмна.

.

В задачах 201 – 210вычислить объём тела, полученного при вращении вокруг оси ОХ фигуры, ограниченной линиями.

201. .	202. .
203. .	204. .
205. .	206. .
207. .	208. .
209. .	210. .

В задачах 211 – 220вычислить объём тела, полученного при вращении вокруг оси ОУ фигуры, ограниченной линиями.

211. .	212. .
213.	214.
215. .	216. .
217. .	218. .
219. .	220. .

Решение типового примера

Вычислить объём тела, полученного вращением эллипса

вокруг оси ОХ.

Р е ш е н и е.

Изобразим тело, полученное при вращении эллипса вокруг оси ОХ (рис. 4).

Рис. 4.

Объём вычислим по формуле .

Из уравнения эллипса выразим и подставим в формулу:

.