Решение типового примера

Найти указанные пределы:

1. Воспользуемся теоремами о пределах частного и алгебраической суммы :

= =

= = .

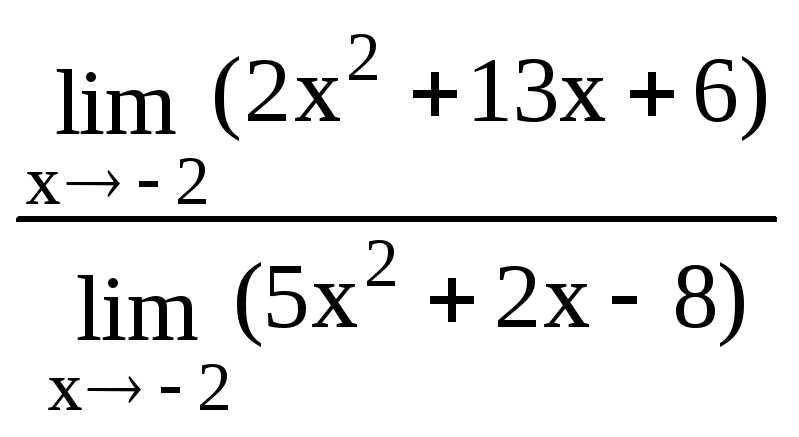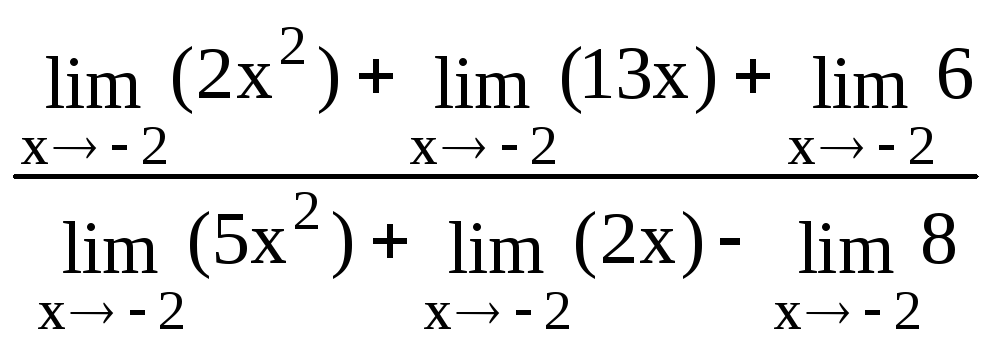2. Непосредственная подстановка предельного значения аргументаx=2 приводит к неопределенности вида. Чтобы раскрыть эту неопределенность, разложим числитель и знаменатель на множители.

Так как , но не совпадает со своим предельным значением, то:

= = = .

3. В этом случае имеем неопределенность вида . Так как в числи­теле и знаменателе стоят многочлены, то для раскрытия неопре­деленности необходимо числитель и знаменатель разделить на наи­высшую степень x из слагаемых многочленов числителя и знаменателя, т.е. на , а затем перейти к пределу:

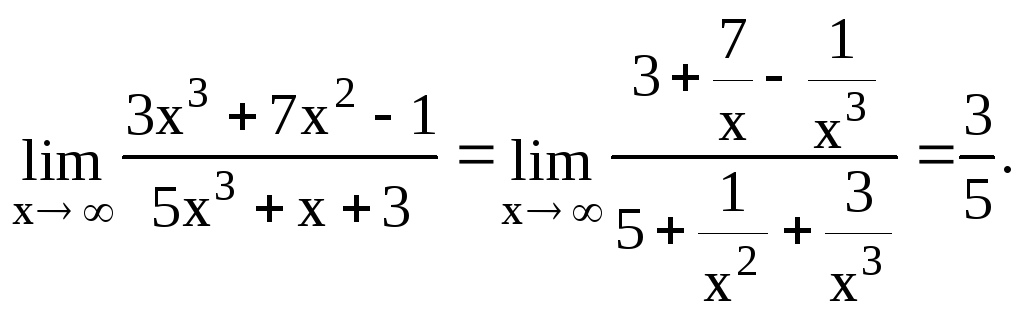
Так как бесконечно малые величины при , то их пределы равны 0.

4. Найти Под знаком предела есть иррациональ-ность в числителе дроби. Непосредственная подстановка предельного значения аргументаприводит к неопределенности вида.

Чтобы раскрыть эту неопределенность, достаточно числитель и знаменатель дроби, стоящей под знаком предела, домножить на выражение, сопряженное числителю дроби:

=

5. Воспользуемся первым замечательным пределом .

Получим

.

6. Найти. Привыражение, а показатель степени стремится к бесконечности. Следовательно, имеем неопределенность вида .Представим основание в виде суммы 1 и некоторой бесконечно малой величины:

Тогда

Положим ; припеременная.

Выразим показатель степени через новую переменную y.

Так как то

Используя второй замечательный предел получим

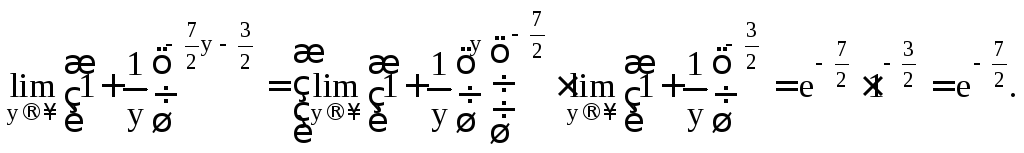
Т е м а 3. Производная

Изучение этой темы следует начать с разбора решений задач, приводящих к понятию производной. Это позволит осмыслить и понять определение производной, условия ее существования, ее геометрический и механический смыслы. Особое внимание необходимо обратить на теоремы и правила, позволяющие упростить вычисление производных. Успешное применение производной при решении задач зависит от усвоения понятий возрастания и убывания функций, наибольших и наименьших значений функции, экстремумов функции, выпуклости и вогнутости кривой.

Вопросы для изучения и самопроверки

1. Производная функции, ее геометрический смысл.

2. Правила дифференцирования функций.

3. Производная сложной, неявно заданной и обратной функций.

4. Дифференцирование функций, заданных параметрически.

5. Дифференциал функции.

6. Производные и дифференциалы высших порядков.

7. Теоремы Ролля, Лагранжа, Коши. Правило Лопиталя.

8. Условия возрастания и убывания функций. Экстремум функции. Необходимое условие экстремума. Достаточные признаки существо- вания экстремума.

9. Наибольшее и наименьшее значения непрерывной на отрезке функции.

10. Выпуклость и вогнутость графика функции. Точки перегиба.

11. Асимптоты кривых.

Задачи контрольной работы

В задачах 61–80найти производные функций:

61.а);	б) ;
в) ;	г) .
62.а);	б) ;
в) ;	г) .
63.а);	б) ;
в) ;	г) .
64.а);	б) ;
в) ;	г) .
65. а);	б) ;
в) ;	г) .
66. а);	б) ;
в) ;	г) .
67. а);	б) ;
в) ;	г) .
68. а);	б) ;
в) ;	г) .
69.а);	б) ;
в ) ;	г) .
70.а);	б) ;
в) ;	г) .
71.а);	б) ;
в)	г) .
72.а);	б) ;
в) ;	г) .
73. а);	б) ;
в) ;	г) .
74. а);	б) ;
в) ;	г) .
75. а);	б) ;
в) ;	г) .
76. а);	б) ;
в) ;	г) .
77.а);	б) ;
в) ;	г) .
78. а);	б) ;
в) ;	г) .
79.а);	б) ;
в) ;	г) .
80. а);	б) ;
в) ;	г) .