Вопросы для изучения и самопроверки

1. Определитель и его свойства.

2. Способы вычисления определителей.

3. Формулы Крамера.

4. Системы координат.

5. Векторы. Линейные операции над векторами.

6. Скалярное, векторное и смешанное произведения векторов и их свойства. Применение скалярного, векторного и смешанного произведений векторов.

7. Расстояние между двумя точками.

8. Деление отрезка в заданном отношении.

9. Виды уравнений прямой на плоскости. Угол между прямыми. Расстояние от точки до прямой.

10.Уравнения плоскости и прямой в пространстве. Угол между плоскостями. Угол между прямой и плоскостью. Расстояние от точки до плоскости.

11.Кривые и поверхности второго порядка, их геометрические свойства.

Задачи контрольной работы

В задачах 1–20 даны координаты вершин треугольникаABC. Найти: 1) длину стороныAB; 2) уравнение стороныABи ее угловой коэффициент; 3) уравнение высотыCD и ее длину; 4) уравнение медианыAE; 5) координаты точкиKпересечения медианы АЕ с высотойCD. Сделать чертеж.

1.	A(–7; –2),	B(5; –11),	C(9; 11).
2.	A(–6; 7),	B(3; –5),	C(8; 5).
3.	A(–4; 8),	B(5; –4),	C(10; 6).
4.	A(–2; 6),	B(7; –6),	C(12; 4).
5.	A(–5; 11),	B(4; -1),	C(9; 9).
6.	A(–3; 9),	B(6; –3),	C(11; 7).
7.	A–7; 10),	B(2; –2),	C(8; 8).
8.	A(–8; 13),	B(1; 1),	C(6; 11).
9.	A(–1; 12),	B(8; 0),	C(13; 10).
10.	A(0; 5),	B(9; –7),	C(14; 3).
11.	A(2; 4),	B(11;–8),	C(16; 2).
12.	A(–4; 8),	B(8; –1),	C(12; 21).
13.	A(–11; 0),	B(1; –9),	C(5; 13).
14.	A(–9; 10),	B(3; 1),	C(7; 23).
15.	A(1; 3),	B(13;–6),	C(17; 16).
16.	A(–8; 7),	B(4;–-2),	C(8; 20).
17.	A(2; 1),	B(14; –8),	C(18; 14).
18.	A(–3; 11),	B(9; 2),	C(13; 24).
19.	A(3; 6),	B(15; –3),	C(19; 19).
20.	A(0; 5),	B(12; –4),	C(16; 18).

Решение типового примера

Пусть A (-4; 10), B (8; 1), C (12; 23).

1.Расстояниеd между точкамиA(x₁; y₁) иB(x₂; y₂) определяется по формуле

.

(1)

Применяя формулу (1), получим:

.

2. Уравнение прямой, проходящей через точки A(x₁; y₁) иB(x₂; y₂), имеет следующий вид:

.

(2)

Подставляя координаты точек A(-4; 10) и B(8; 1) в формулу (2), получим уравнение стороныAB:

		(АВ)

Угловой коэффициент прямой AB ;

3. Уравнение прямой, проходящей через данную точку С(x_1;y₁) в заданном направлении, имеет вид:

.

(3)

Так как прямая СDперпендикулярна прямой АВ, тоk_СD=–1/k_AB

т.е. k_СD=4/3. Подставив координаты точки С и найденный угловой коэффициент высоты СD в уравнение (3), получим

(CD).

Расстояние от произвольной точки М(x_0;y₀) до прямойAx+By+C=0 вычисляется по формуле

.

(4)

Длина высоты СD равна расстоянию от точки С до прямой АВ. Учитывая формулу (4), получим

4. Определим координаты точки E, которая является серединой стороныBC, применяя формулы деления отрезка на две равные части:

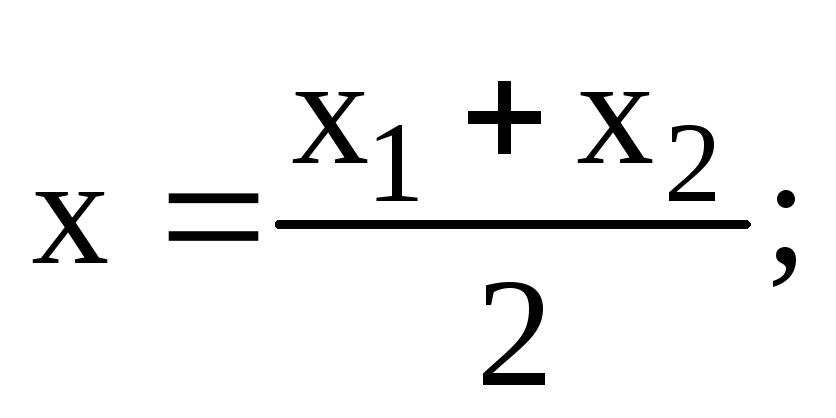
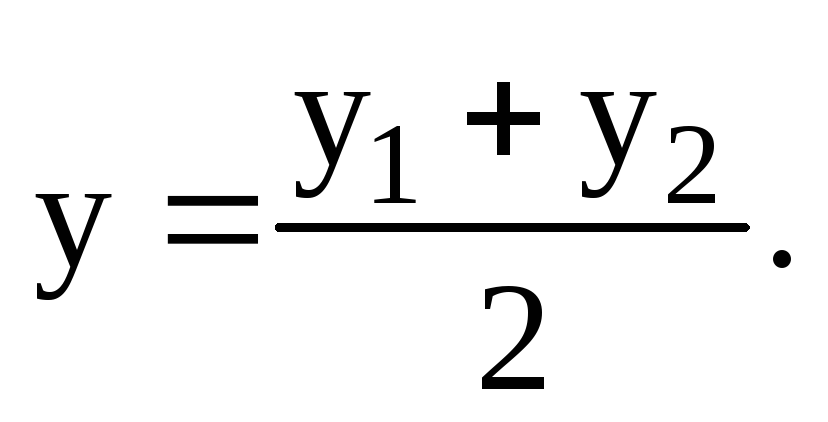
(5)

Следовательно, E(10;12).

Тогда уравнение медианы будет иметь вид

(AE).

5. Чтобы найти координаты точки К (пересечения высоты CDи медианыAE), решим систему следующих уравнений:

x=3, y=11; K(3; 11).

Сделаем чертеж : ( рис. 1).

Рис.1.

В задачах 21–40 даны координаты вершин пирамидыABCD. Требуется :

1) записать векторы ,ив системе орти найти модули этих векторов;

2) найти угол между векторами и

3) найти проекцию вектора на вектор;

4) найти площадь грани ABC;

5) найти объем пирамиды ABCD;

6) составить канонические уравнения прямой АВ;

7) составить уравнение плоскости проходящей через точку С перпендикулярно вектору ;

8) найти точку пересечения полученной плоскости и прямой АВ

21.	A(4; 0; 6),	B(8; 2; 2),	C(5; –1; 2),	D(6; 2; 7).
22.	A(0; 3; 4),	B(4; 5; 0),	C(1; 2; 0),	D(2; 5; 5).
23.	A(3; –2; 8),	B(7; 0; 4),	C(4; –3; 4),	D(5; 0; 9).
24.	A(1; –1; 7),	B(5; 1; 3),	C(2; –2; 3),	D(3; 1; 8).
25.	A(–2; 2; 3),	B(2; 4; –1),	C(–1; 1; –1),	D(0; 4; 4).
26.	A(–1; 4; 2),	B(3; 6; –2),	C(0; 3;–2),	D(1; 6; 3).
27.	A(–3; 1; 9),	B(1; 3; 5),	C(–2; 0; 5),	D(–1; 3; 11).
28.	A(2; 5; 1),	B(6; 7; –3),	C(3; 4; –3),	D(4; 7; 2).
29.	A(5;–3; 10),	B(9; –1; 6),	C(6; –4; 6),	D(7; –1; 11).
30.	A(6; 6; 5),	B(10; 8; 1),	C(7; 5; 1),	D(8; 8; 6).
31.	A(–2; 2; 6),	B(0; 3; 4),	C(8; 13; 8),	D(–1; 3; 7).
32.	A(–4;–3; 7),	B(-2; –2; 5),	C(6; 8; 9),	D(–3; –2; 8).
33.	A(2; 0; 5),	B(4; 1; 3),	C(12; 11; 7),	D(3; 1; 6).
34.	A(–1;–6; 4),	B(1;–5; 2),	C(9; 5; 6),	D(0; –5; 5).
35.	A(3;–4; –2),	B(5; –3;–4),	C(13; 7; 0),	D(4; –3;–1).
36.	A(1; –1;0),	B(3; 0; –2),	C(11; 10; 2),	D(2; 0; 1).
37.	A(–3; 4; 8),	B(-1; 5; 6),	C(7; 15; 10),	D(–2; 5; 9).
38.	A(0; 5; 3),	B(2; 6; 1),	C(10; 16; 5),	D(1; 6; 4).
39.	A(–5;–7; 1),	B(–3;–6; –1),	C(5; 4; 3),	D(–4; –6; 2).
40.	A(4; –5;–1),	B(6;–4; –3),	C(14; 6; 1),	D(5; –4; 0).