
- •Введение
- •Тема 1. Элементы векторной алгебры
- •Решение типового примера
- •Тема 2. Элементы аналитической геометрии на плоскости и в пространстве
- •Решение типового примера
- •Решение типового примера
- •Тема 3. Введение в мАтематический анализ функции одной переменной
- •Вопросы для изучения и самопроверки
- •Решение типовых примеров
- •Тема 4. Дифференциальное исчисление функции одной переменной и его применение к исследованию функции
- •Вопросы программы для изучения и самопроверки
- •Решение типовых примеров
- •Правила дифференцирования
- •Решение типового примера
- •Тема 5. ФункциИ двух независимых переменных
- •Вопросы для изучения и самопроверки
- •Решение типовых примеров
- •Решение типового примера
- •Тема 6. Неопределенный интеграл
- •Вопросы для изучения и самопроверки
- •Решение типовых примеров
- •Основная таблица интегралов
- •Тема 7. Определенный интеграл и его применение для вычисления площадей плоских фигур
- •Вопросы для изучения и самопроверки
- •Решение типового примера
- •Решение типового примера
- •Тема 8. Дифференциальные уравнения первого порядка
- •Вопросы для изучения и самопроверки
- •Решение типового примера
- •Решение типового примера
- •Тема 9. Основные понятия и задачи теории
- •Вопросы для изучения и самопроверки
- •Решение типовых примеров
- •Решение типового примера
- •Решение типового примера
- •Решение типового примера
- •Решение типового примера
Решение типового примера
Пусть А(4;-1;-3), В(2;-3;-2), С(-3;2;3).
1. Канонические уравнения прямой в пространстве имеют следующий вид:
![]() ,
,
где х , у , z– координаты точки, через которую проходит прямая;
m,
n,
p–координаты
направляющего вектора этой прямой; в
данном случае это будут координаты
вектора
![]() .
Тогда уравнения прямой
.
Тогда уравнения прямой![]()
2. Уравнение
плоскости, проходящей через данную
точку М(х,y,z),
перпендикулярно данному вектору
![]() (A,B,C):
(A,B,C):
А(х-х0 )+В(у-у0 )+С(z-z0 )=0.
Тогда уравнение плоскости Р: -2(х+3)-2(у-2)+(z-3)=0.
После упрощения: -2х-2у+z -5=0 или 2х+2у-z +5=0.
3. Для того, чтобы найти точку пересечения прямой и плоскости,
нужно уравнения прямой представить в параметрическом виде:
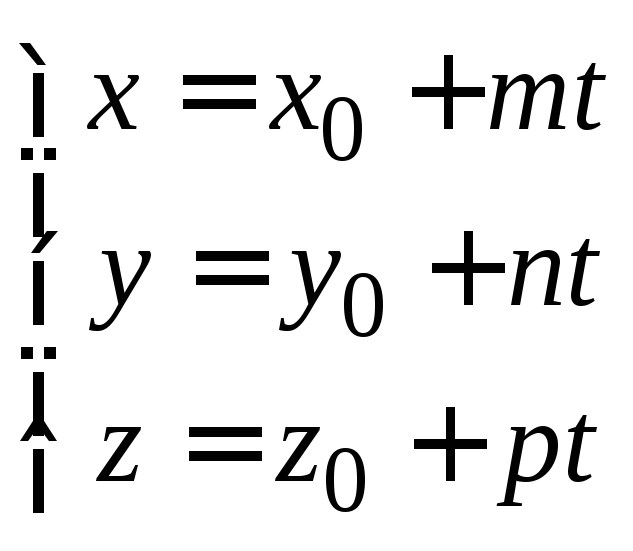 , где t
–параметр.
, где t
–параметр.
Уравнение
АВ в параметрическом виде:
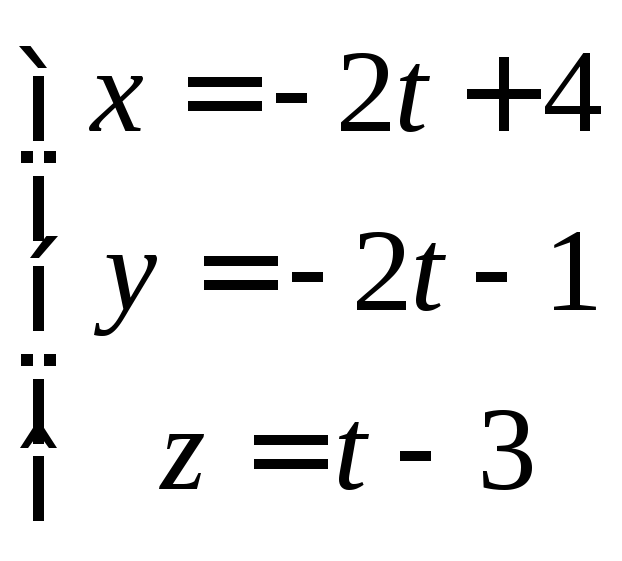 .
.
Подставим
эти значения в уравнение плоскости Р:
![]() ,
,![]() ,
,
![]() ,
,
![]() .
Тогда
.
Тогда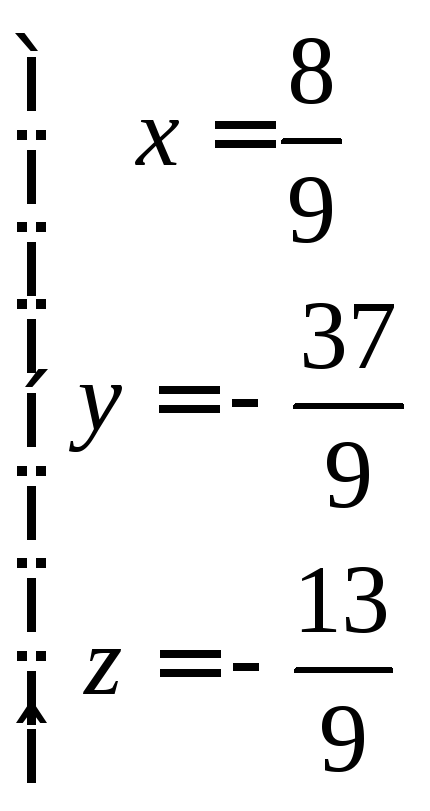 ,
т.е. точка пересечения М прямой АВ и
плоскости Р имеет координаты:
,
т.е. точка пересечения М прямой АВ и
плоскости Р имеет координаты:![]() .
.
4. Расстояние от
точки
![]() до плоскости
до плоскости![]() вычисляем по формуле:
вычисляем по формуле:![]() .
.
Найдем
расстояние от точки А до плоскости Р:
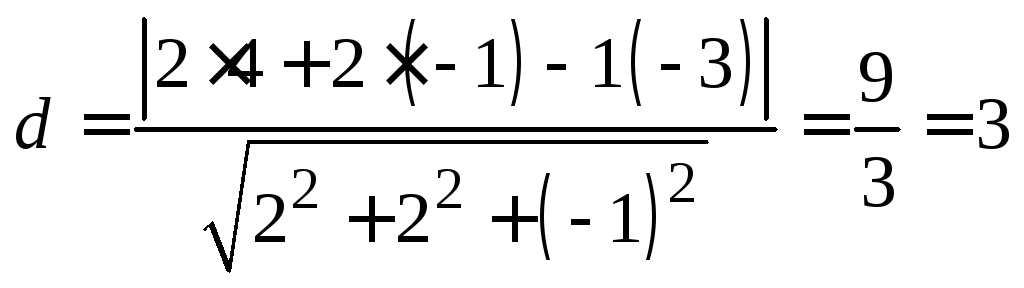 .
.
Тема 3. Введение в мАтематический анализ функции одной переменной
Для успешного усвоения этой темы необходимо разобраться в фундаментальном понятии математического анализа – понятии функции, изучить способы задания функции, свойства основных элементарных функций. При исследовании и анализе поведения функций не обойтись без понятий предела функции, бесконечно малой величины, ограниченной и непрерывной функций. Теоремы о пределах, замечательные пределы играют особую роль при решении задач по этой теме.
Вопросы для изучения и самопроверки
1. Множество действительных чисел. Функция, бластьопределения функции, способы задания функции.
2. Основные элементарные функции, их свойства и графики.
3. Сложные и обратные функции, их графики.
4. Предел функции в точке и на бесконечности. Теоремы о преде-лах. Замечательные пределы.
5. Пределы монотонных функций.
6. Непрерывность функций в точке, на интервале.
7. Непрерывность основных элементарных функций.
8. Бесконечно малые и бесконечно большие функции, их свойства. Сравнение бесконечно малых.
9. Свойства непрерывных на отрезке функций.
Задачи 61–80. Найти пределы заданных функций.
|
61.
а)
|
при
|
|
б)
|
в)
|
|
62.
а)
|
при
|
|
б)
|
в)
|
|
63.
а)
|
при
|
|
б)
|
в)
|
|
64.
а)
|
при
|
|
б)
|
в)
|
|
65.
а)
|
при
|
|
б)
|
в)
|
|
66.
а)
|
при
|
|
б)
|
в)
|
|
67.
а)
|
при |
|
б)
|
в)
|
|
68.
а)
|
при
|
|
б)
|
в)
|
|
69.
а)
|
при
|
|
б)
|
в)
|
|
70.
а)
|
при
|
|
б)
|
в)
|
|
71.
а)
|
при
|
|
б)
|
в)
|
|
72.
а)
|
при
|
|
б)
|
в)
|
|
73.
а)
|
при
|
|
б)
|
в)
|
|
74.
а)
|
при
|
|
б)
|
в)
|
|
75.
а)
|
при
|
|
б)
|
в)
|
|
76.
а) |
при
|
|
б)
|
в)
|
|
77.
а)
|
при
|
|
б)
|
в)
|
|
78.
a)
|
при
|
|
б)
|
в)
|
|
79.
a)
|
при
|
|
б)
|
в)
|
|
80.
а) |
при
|
|
б)
|
в)
|
