Решение типового примера

Процент всхожести семян пшеницы равен 90%. Найти вероятность того, что из 500 посеянных семян взойдут от 400 до 440 семян.

Р е ш е н и е. Если вероятность появления события А в каждом из n испытаний постоянна и равна р, то вероятность того, что событие А появится не менее k₁ раз и не более k₂ раз определяется по интегральной теореме Лапласа, которая имеет формулу

где 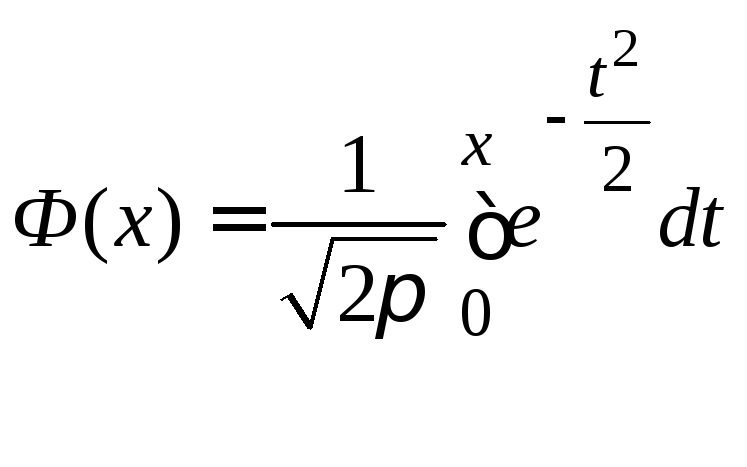– функция Лапласа.

Значение этой функции для положительных значений х даны в приложении 2. При отрицательных значениях х в силу нечетности функции :

_.

По условию задачи n=500; p=90%=0,9; q=1-0,9=0,1; k₁=400; k₂=440.

Находим значения х₁ и х₂.

. .

Тогда .

З

.

адачи 321–340. Дискретная случайная величина Х задана своим законом распределения. Необходимо: 1) построить многоугольник распределения; 2) cоставить функцию распределения F(x) и построить ее график; 3) найти числовые характеристики СВ Х: а) математическое ожидание; б)дисперсию; с) среднее квадратическое отклонение.

321.	Х	-4	-1	2	3	5
	Р	0,1	0,3	0,2	0,3	0,1

322.	Х	-3	-1	2	3	4 .
	Р	0,2	0,1	0,3	0,2	0,2

323.	Х	-5	-3	1	2	4
	Р	0,3	0,1	0,2	0,3	0,1

.

324.	Х	-2	1	3	5	6
	Р	0,4	0,1	0,1	0,2	0,3

.

325.	Х	-2	-1	3	5	7
	Р	0,2	0,4	0,1	0,2	0,1

.

.

326.	Х	-4	-2	1	3	5
	Р	0,3	0,1	0,3	0,2	0,1

327.	Х	-3	-1	3	5	6
	Р	0,3	0,1	0,2	0,1	0,2

.

328.	Х	-5	-2	2	3	6
	Р	0,1	0,4	0,2	0,1	0,2

.

.

.

329.	Х	-2	-1	3	5	6
	Р	0,3	0,1	0,2	0,1	0,3

330.	Х	-3	-2	1	4	5
	Р	0,2	0,1	0,2	0,3	0,2

.

331.	Х	-4	-3	2	3	5
	Р	0,1	0,3	0,2	0,3	0,1

.

332.	Х	-5	-4	2	3	6
	Р	0,2	0,3	0,1	0,3	0,1

.

333.	Х	-2	-1	3	5	7
	Р	0,2	0,1	0,1	0,4	0,2

.

334.	Х	-3	-1	0	2	4
	Р	0,3	0,1	0,2	0,1	0,3

.

335.	Х	-4	-2	1	2	5
	Р	0,2	0,4	0,1	0,1	0,2

.

336.

336.	Х	-5	-3	1	2	4
	Р	0,2	0,1	0,4	0,2	0,1

.

337.	Х	-2	0	3	4	7
	Р	0,1	0,2	0,4	0,2	0,1

.

.

.

338.	Х	-3	-2	1	3	5
	Р	0,2	0,1	0,2	0,4	0,1

339.	Х	-5	-3	1	3	4
	Р	0,3	0,1	0,1	0,3	0,2

.

340.	Х	-4	-2	1	3	6
	Р	0,3	0,1	0,2	0,3	0,1

.

Решение типового примера

ДСВ. Х задана своим законом распределения

X	-2	1	3	5	6 .
P	0,1	0,3	0,1	0,3	0,2

1. Построить многоугольник распределения .

2. Составить функцию распределения , построить ее график.

3. Найти .

Р е ш е н и е. 1. В системе координат ОХУ по оси ОХ откладываем возможные значения случайной величины, по оси ОУ – их соответствующие вероятности. Соединив полученные точки отрезками ломаной, получим многоугольник распределения данной СВ Х (рис.3).

х

-2

Р

Рис.3.

2. Функция распределения . Составимдля нашей задачи:

для ;

для ;

для ;

для

=

для

=

для

Таким образом имеет вид: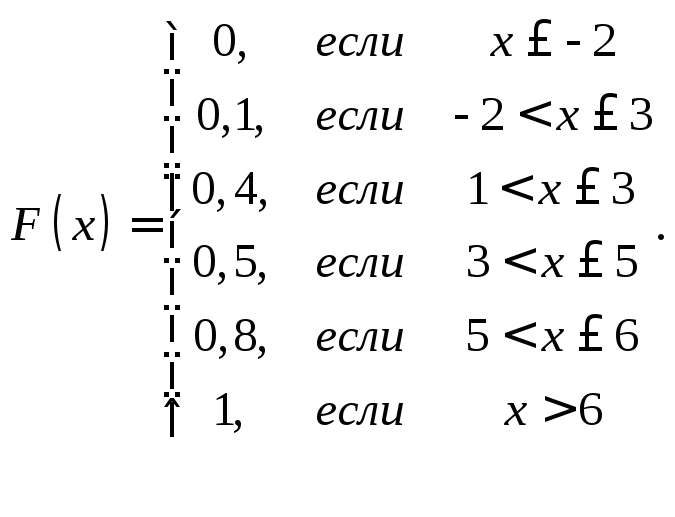

Построим график (рис.4).

F(x)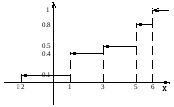

Рис. 4.

3. Найдем числовые характеристики данной случайной величины Х:

а) математическое ожидание М(Х) вычисляется по формуле ,

б) дисперсия вычисляется по формуле

.

Вычислим

Тогда .

в) среднее квадратическое отклонение .

Задачи 341–360. Непрерывная случайная величина Х задана функцией распределения F(x). Требуется: а) найти плотность распределения вероятностей f (x); б) построить графики функции f(x) и F(x); в) найти математическое ожидание М(Х) и дисперсию Д(Х).

341..	342..
343..	344..
345..	346..
347. .	348. .
349. .	350. .
351. .	352. .
353. .	354. .
355. .	356. .
357. .	358. .
359. .	360. .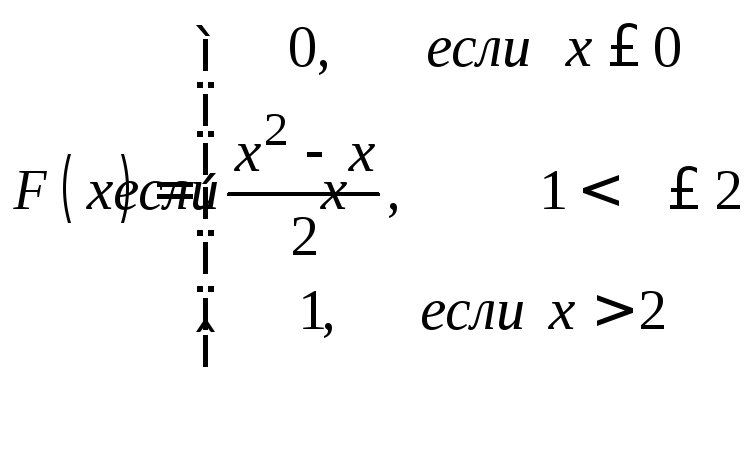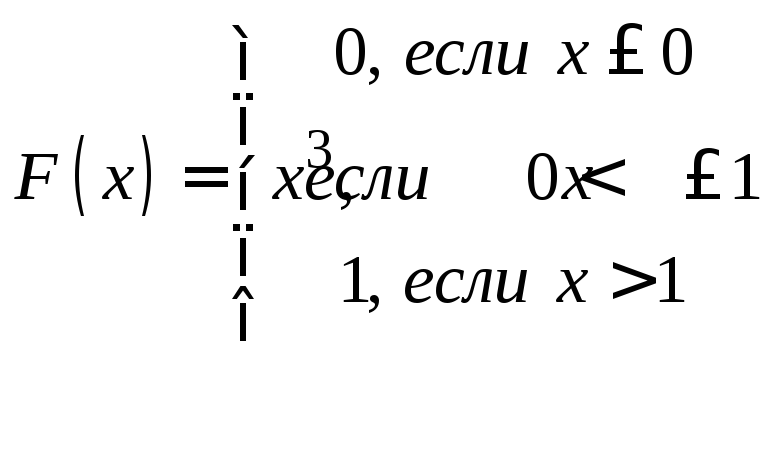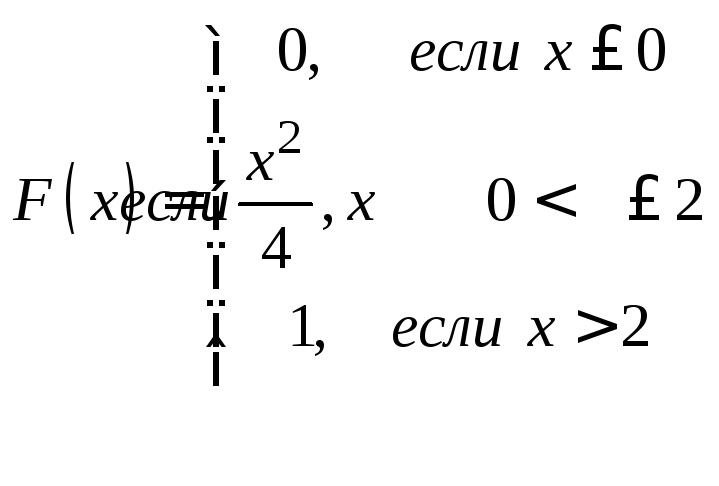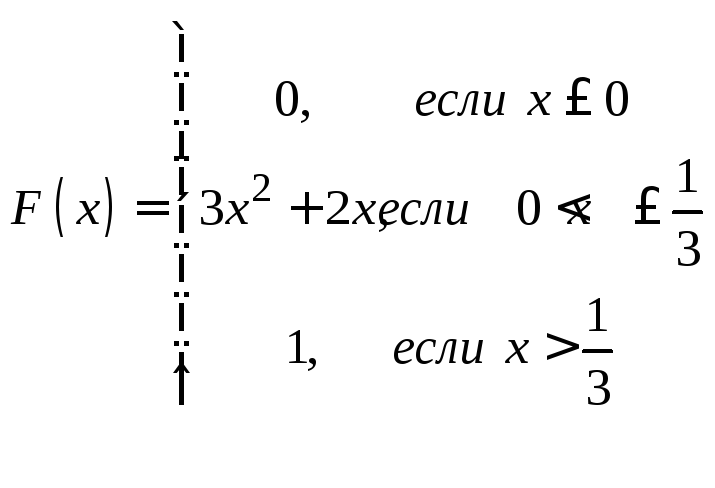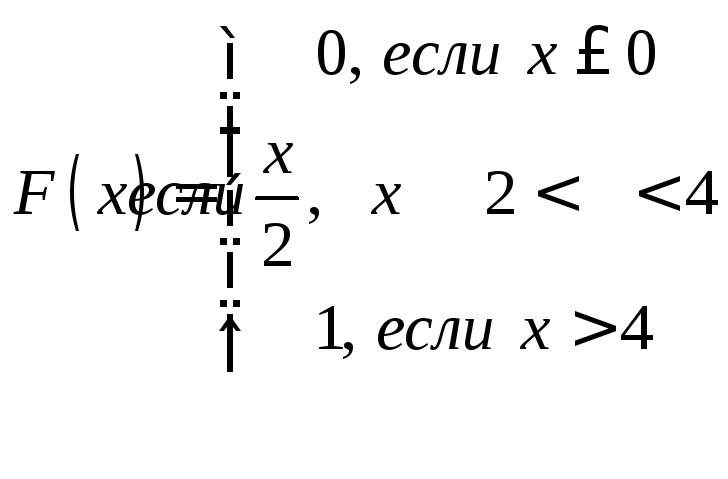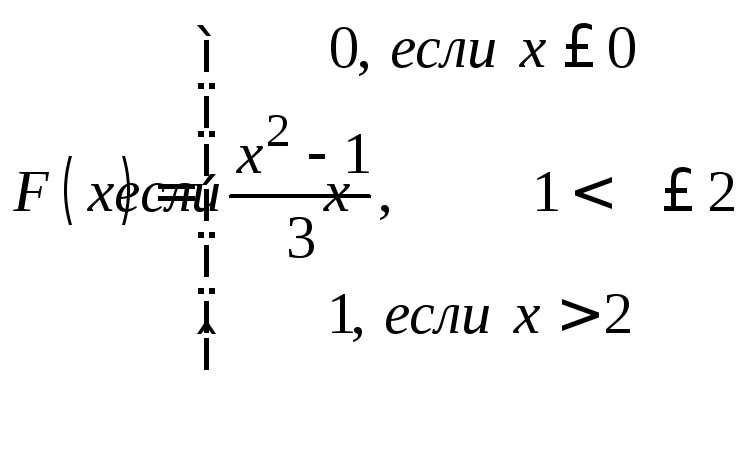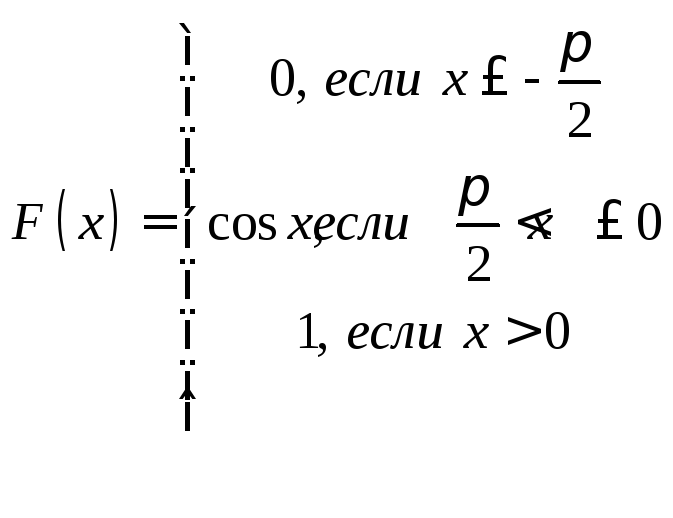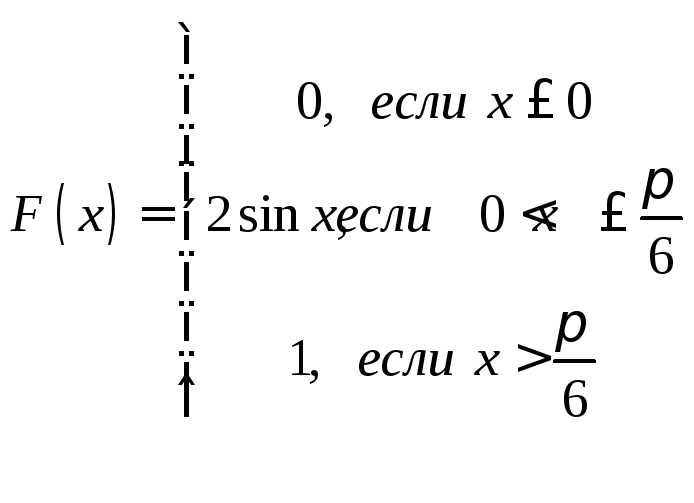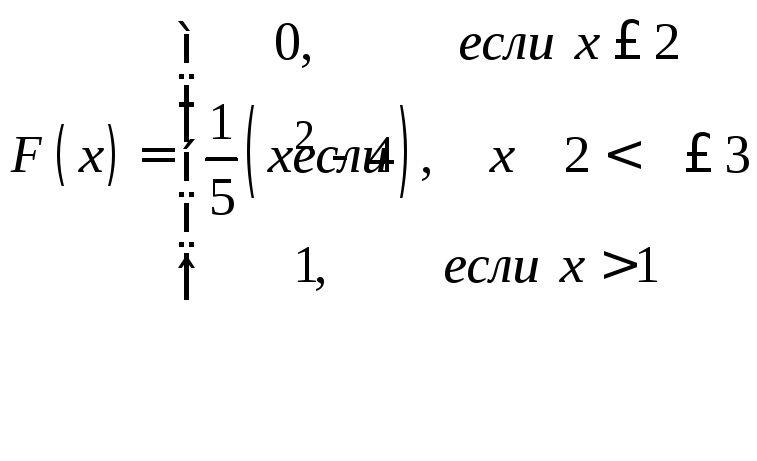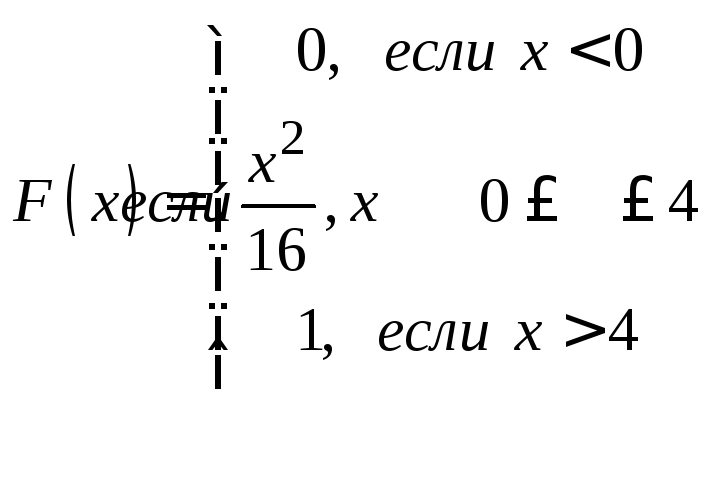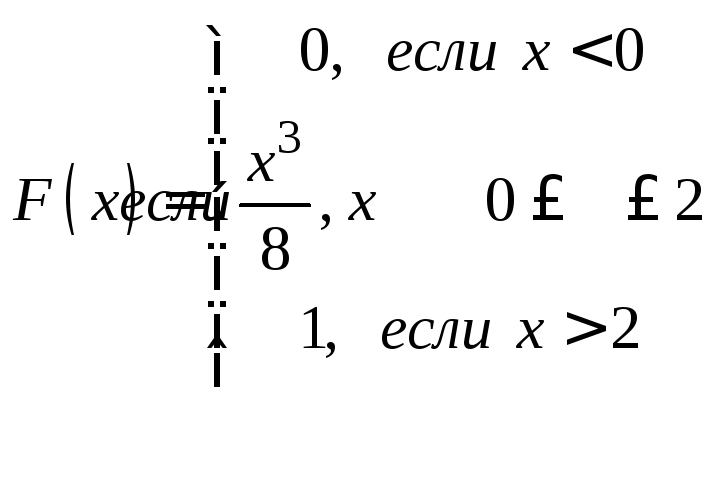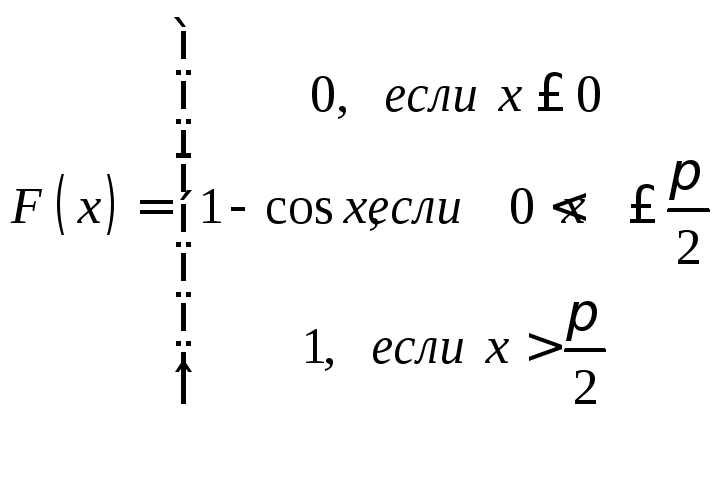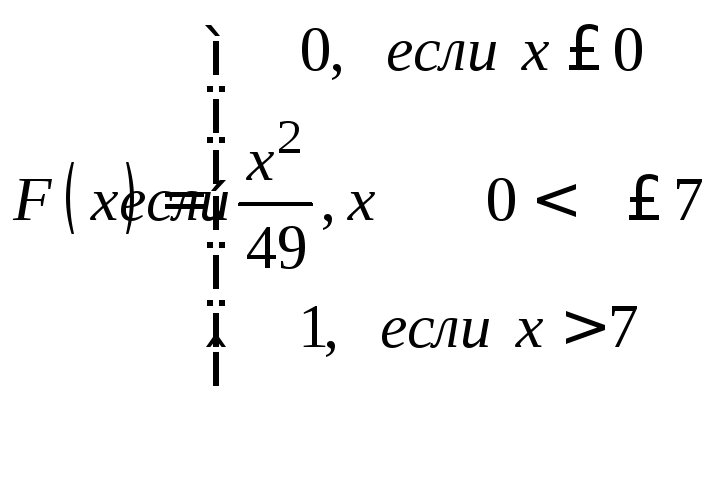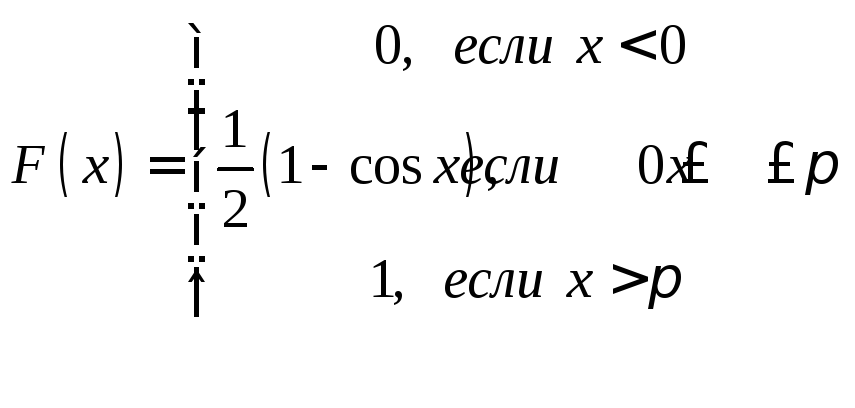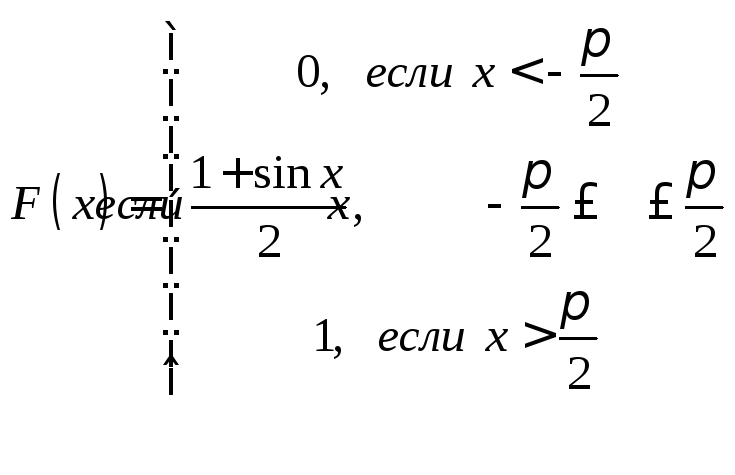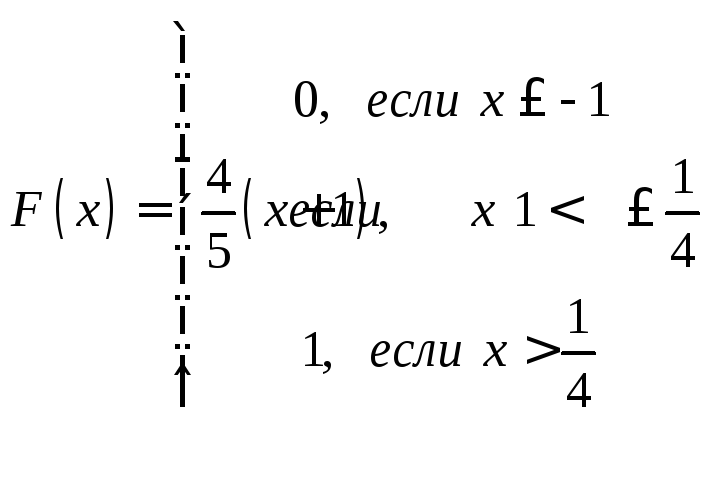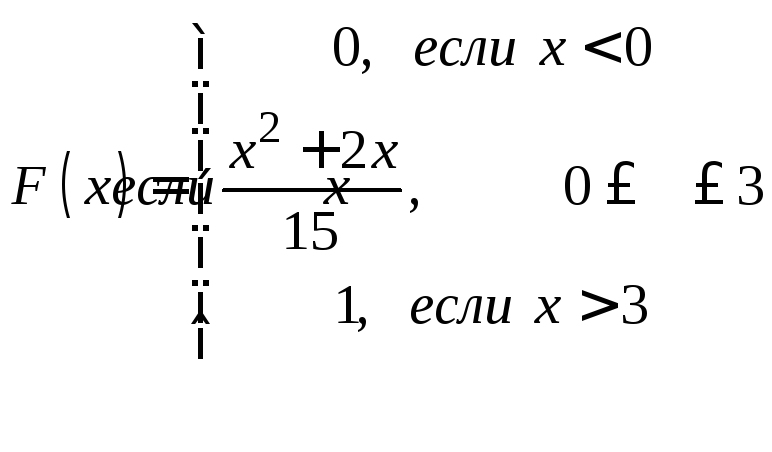