Решение.
а) Событие А – наудачу выбранный студент будет оттестован на “отлично”. Очевидно вероятность А колеблется от 0,1 до 0,9 и зависит от того какой студент (отличник, хорошист или посредственник) проходит аттестацию. Воспользуемся формулой полной вероятности (5), в которой события Hi называют гипотезами (несовместны и образуют полную группу). От случаев гипотезы отличаются тем, что требование равновозможности не обязательно.
В нашей задаче в качестве гипотез будут:
Н1
– отличник, Н2
– хорошист, Н3
– посредственник. Их вероятности по
формуле (2)
;
;
.
Условие вероятности
по условию задачи
;
;
.
.
б) Вероятность того, что студент прошедший аттестацию на “отлично” из хорошистов есть условная вероятность события Н2 от А и рассчитывается по формуле (6).
.
Задача 3. Плотность вероятности случайной величины Х заданна выражением:
.
Найти:
а) постоянный параметр С
б) Функцию распределения F(X)
в) математическое ожидание М[X]
г) среднее квадратическое отклонение G[X]
д) вероятность попадания Х в (0; 0.5)
е) построить графики р(х) и F(x).
Решение.
а) По свойству
плотности вероятности
,
учитывая, что при x<0
и x>1
p(x)=0,
получим
.
После интегрирования и применения
формулы Ньютона-Лейбница, получим
уравнение относительно С.
С=
5
=1,
4
|
|
|
|
|
;
,
.
б) Функция распределения с плотностью распределения связаны формулой (14).
Так как р(х)¹0 только для 0< х £1, то по свойствам F(x) имеем: F(x)=0 при х<0; F(x)=1 при х>1. Для 0< х £1
.
Итак,
е)
д) Вероятность попадания случайной величины в заданный интервал (a, b) можно найти по одной из формул (15)
.
в) Для непрерывной случайной величины математическое ожидание расчитывается по формуле (16(б)). В нашем случае
так как вне (0; 1)
p(x)=0
.
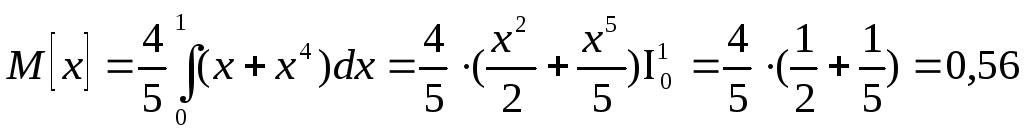г) Сначала находим Д[x] по формуле (17(б))
Тогда G[x] по формуле (18) будет
Задача 4. Рост мужчины определенной возрастной группы распределен по нормальному закону с математическим ожиданием m=177 и средним квадратическим отклонением G=5. Какую долю костюмов в общем объеме производства следует предусмотреть для второго роста (164 – 170)?
Решение.
Ответ на поставленный вопрос сводится к нахождению вероятности попадания нормально распределенной случайной величины в заданный интервал, которая определяется формулой (27). В нашем случае:
Здесь использовано свойство нечетности функции Лапласа (26), а ее значения ф(2,6) и
ф(1,4) взяты из приложения 2.
Следовательно,
долю костюмов второго роста в процентах
следует предусмотреть в количестве
%
7,6%.
Задача 5. На заводе для учета потока заявок на инструмент в течение часа регистрировалось число рабочих, обратившихся в кладовую за необходимым инструментом. Наблюдения проводились 100 раз и представлены следующей таблицей:
|
7 |
0 |
0 |
1 |
2 |
4 |
3 |
3 |
1 |
2 |
2 |
2 |
2 |
5 |
3 |
2 |
2 |
3 |
3 |
1 |
|
5 |
1 |
1 |
2 |
4 |
2 |
4 |
1 |
3 |
1 |
2 |
2 |
3 |
1 |
2 |
0 |
2 |
6 |
1 |
3 |
|
1 |
1 |
2 |
6 |
1 |
6 |
1 |
3 |
5 |
3 |
3 |
4 |
4 |
2 |
3 |
1 |
3 |
3 |
0 |
1 |
|
4 |
1 |
1 |
1 |
4 |
4 |
2 |
4 |
4 |
2 |
6 |
2 |
2 |
2 |
3 |
3 |
1 |
1 |
1 |
1 |
|
1 |
0 |
3 |
3 |
1 |
3 |
3 |
2 |
2 |
2 |
6 |
5 |
2 |
1 |
2 |
5 |
2 |
1 |
1 |
0 |
Требуется:
1. Составить дискретный статистический ряд распределения частот и частостей случайной величины Х – числа заявок.
2. Построить полигон частостей.
3. Вычислить числовые характеристики: среднюю выборочную, выборочную дисперсию, выборочное квадратическое отклонение.
4. По виду графического изображения и значениям точечных оценок обосновать гипотезу о пуассоновском распределении заявок.
5. Написать аналитическое выражение закона.
6. Проверить степень согласия теоретического и эмпирического распределения с помощью критерия согласия Пирсона при уровне значимости a=0,05.