
- •СОДЕРЖАНИЕ
- •ВВЕДЕНИЕ
- •1. Природа сил химической связи
- •1.1 Методы анализа сложных молекул
- •1.1.1 Метод валентных связей
- •1.1.2 Метод молекулярных орбиталей
- •1.1.3 Заключение
- •2. Структура энергетических уровней молекул
- •2.1 Потенциальные кривые электронных состояний молекул
- •2.2 Колебательные уровни энергии молекул
- •2.3 Вращательные уровни энергии молекул
- •2.4 Заключение
- •3. Молекулярные спектры
- •3.1 Общие характеристики молекулярных спектров
- •3.1.1 Вращательные спектры молекулы.
- •3.1.2 Колебательно-вращательные спектры молекулы
- •3.1.3 Электронные спектры молекулы.
- •3.2 Спектр поглощения двухатомной молекулы йода
- •4. Экспериментальная часть
- •4.1 Описание установки
- •4.2 Обработка результатов. Задание.
- •4.3 Вопросы к отчету
- •Литература
Лабораторная работа № 1
СПЕКТР ПОГЛОЩЕНИЯ ПАРОВ ЙОДА
ВВЕДЕНИЕ
Понятие молекулы впервые было введено в химии. Молекула – наименьшая частица вещества, обладающая его основными химическими свойствами и способная существовать самостоятельно. Молекула состоит из одинаковых или различных атомов соединенных в единое целое силами межатомных взаимодействий (химическими связями).
Исследования атомных спектров показали, что все основные закономерности, наблюдаемые в них, обусловлены особенностями структуры электронной оболочки и элек-
тронных состояний |
атома. Химические свойства атомов – способность к образованию тех |
или иных молекул |
– объясняются также свойствами их электронных оболочек. Однако ре- |
зультат проявления химических свойств, а, следовательно, и сами эти свойства принадлежат не одному, а совокупности атомов, взаимодействие которых приводит к образованию молекулы. В процессе химического взаимодействия, в механизме химической связи важное значение имеют те электроны атома, которые характеризуются сравнительно малыми энергиями при изменении их состояний. Такими электронами являются внешние электроны атома. Действительно, электроны, находящиеся на внутренних заполненных оболочках, в образовании химической связи практически участия не принимают.
В отдельных случаях можно химическое взаимодействие свести к электростатическим силам. Так в ионных соединениях валентные электроны атомов при взаимодействии переходят от одного атома к другому. При этом атомы превращаются в ионы с различными электрическими зарядами, взаимодействие которых описывается законом Кулона. Образуется так называемая ионная связь.
Поскольку кулоновское взаимодействие в первом приближении не искажает электронную структуру ионов, то можно считать, что при наличии ионной связи ионы в основном сохраняют свою индивидуальность в молекуле.
Однако часто при |
образовании молекул не наблюдается переход электронов от од- |
|
ного атома к другому, и, |
следовательно, |
ионная связь отсутствует. К таким молекулам от- |
носятся, например, молекулы O2 , N2 , Cl2 |
и др. Естественно, что для таких молекул харак- |
|
терным является другой тип связи – ковалентный, в котором природа сил взаимодействия не может быть объяснена законами электростатики
Следовательно, мы можем разделить все химические связи на два класса – ионную и ковалентную. Такая классификация, безусловно, является определенным упрощением. Реальные химические связи могут характеризоваться различными степенями (ионности) и (ковалентности).
1. Природа сил химической связи
1.1 Методы анализа сложных молекул
Существует утверждение, что силы связи между атомами в молекуле могут быть поняты только на основе квантовомеханического рассмотрения этой задачи. Однако это утверждение нуждается в пояснении. Этот вывод в известном смысле справедлив, но существует очень важная теорема, доказанная независимо Фейнманом и Хеллманом и названная их именами, утверждающая, что силы, связывающие атомы в молекулу, представляют собой не что иное, как электростатические силы. Суть теоремы Фейнмана-Хеллмана заключается в том, что если известно распределение вероятности электрона в молекуле, то вычисление энергии системы (сил связи) представляет собой чисто классическую электростатическую
3
задачу. Конечно, рассмотрение проблемы распределения заряда в молекуле немыслимо без квантовой механики. Но если распределения заряда в молекуле известно, то остающаяся задача является чисто классической.
Связи в многоатомных молекулах представляют собой сложную картину, которую можно рассмотреть с помощью двух подходов: в представлениях модели валентных связей и
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
метода молекулярных орбиталей. Оба подхода являются |
||||||||||||||||||||||||
|
|
|
|
|
-e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
основными |
приближенными |
методами расчета химиче- |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
r12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
-e |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ской связи. Познакомимся кратко с этими методами. |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
rB1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обычно, в целях упрощения задачи, при описании |
||||||||||||||||||||||
|
|
rA1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rB2 |
|
|
|
|
молекулы |
пренебрегают ее вращательным движением и |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
rA2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
всеми взаимодействиями электронных и колебательных |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
движений с вращательным, что допустимо из-за малости |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
rAB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
A |
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
энергии вращательного движения молекулы по сравнению |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
Рис.1 Схема молекулы |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
с |
|
электронной |
|
и колебательной энергиями. Молекулу |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
водорода |
|
|
|
|
|
|
|
|
|
|
|
|
|
обычно описывают в системе координат, в которой она |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
покоится. В этом случае уравнение Шредингера для |
||||||||||||||||||||||||
гоатомной молекулы будет иметь видмногоатомной молекулы будет иметь вид |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
∂2 ψ |
∂2 ψ |
∂2 ψ |
|
|
|
|
|
1 |
|
∂2 |
ψ |
|
|
∂2 ψ |
∂2 ψ |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ |
2 |
|
+ |
|
|
2 + |
|
2 |
|
+ ∑ |
|
|
|
|
|
|
2 |
+ |
|
|
2 + |
2 + |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
me i |
|
|
∂xi |
|
|
|
|
∂yi |
∂zi |
|
|
A |
|
|
mA |
∂xA |
|
|
∂yA |
∂zA |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8π |
2 |
|
|
|
|
e |
2 |
|
|
|
z |
|
e |
2 |
|
|
|
z |
|
z |
|
e |
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
A |
B |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
E |
− |
|
|
|
+ |
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
ψ = 0 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h 2 |
∑ r |
|
∑ r |
|
|
|
∑ |
|
|
r |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ij |
|
|
|
|
|
|
|
|
|
|
1.1 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ij |
|
iA |
|
iA |
|
|
AB |
|
|
|
AB |
|
|
|
|||||||||
где ψ – волновая функция молекулы; me , MA |
– массы электронов и ядер атомов соответст- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
венно; rij – расстояние между |
|
|
i-м |
j-м электронами; riA , rAB |
|
– расстояния между i-м элек- |
|||||||||||||||||||||||||||||||||||||||||||||||||
троном и A-м ядром и A-м и B-м ядрами соответственно; zA , zB |
– заряды ядер. В уравне- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
нии (1.1) первый член соответствует кинетической энергии электронов, причем в нем суммирование ведется по всем электронам молекулы. Второй член характеризует кинетическую (колебательную) энергию ядер. Третий член описывает потенциальную энергию отталкивания электронов друг от друга (второе слагаемое в скобках), энергию притяжения электронов к ядрам (третье слагаемое) и энергию отталкивания ядер (четвертое слагаемое). В них суммирование ведется по всем возможным различным сочетаниям пар частиц. Точное решение уравнения (1.1) невозможно, поэтому при его решении приходится делать ряд допущений. Борн и Оппенгеймер показали, что уравнение (1.1), поскольку me << MA , достаточно точно
можно аппроксимировать двумя уравнениями (адиабатическое приближение). Первое из них
|
∂ |
|
ψ ∂ |
|
ψ ∂ |
|
ψ |
8π |
|
m |
|
|
|
e |
|
|
|
z e |
|
|
|
||||||
|
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
+ |
|
|
|
+ |
|
|
|
+ |
|
|
|
e |
E − |
|
|
|
+ |
|
A |
|
ψ = 0 |
|
∑ |
∂x2 |
∂ |
2 |
∂z2 |
h2 |
|
∑ r |
|
∑ r |
|
|
||||||||||||||||
|
|
|
|
|
|
ij |
|
|
|
1.2 |
|||||||||||||||||
i |
|
|
i |
|
|
|
i |
|
|
|
i |
|
|
|
|
|
ij |
|
|
iA |
iA |
|
|
||||
описывает движение электронов в поле неподвижных ядер (член zAzB/rAB |
можно в этом |
||||||||||||||||||||||||||
случае не учитывать, так как он превращается в константу и его следует прибавить ко всем значениям E после решения уравнения (1.2)). Второе уравнение описывает движение ядер и оно важно при рассмотрении при рассмотрении колебательных уровней молекулы.
Для иллюстрации путей решения уравнения (1.2) рассмотрим самую простую молекулу
– молекулу водорода. Для молекулы уравнение (1.2) будет иметь вид (см. рис. 1)
∑ ∂ |
|
ψ2 |
+ |
∂ |
|
ψ2 |
+ |
∂ |
|
ψ2 |
+ |
8π |
|
2me E − |
e |
|
+ |
e |
|
+ |
e |
|
+ |
e |
|
− e |
|
ψ = 0 |
|
|||
2 |
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|
2 |
|
|
2 |
|
|
2 |
|
|
i=1 |
∂xi |
|
∂yi |
|
∂zi |
|
h |
|
|
rA1 |
|
rB1 |
|
rA2 |
|
rB2 |
|
r12 |
|
1.3 |
||||||||||||
4

1.1.1 Метод валентных связей |
|
B ( |
|
) |
|
||
Пусть ψ |
A ( ) |
является волновой функцией 1s-состояния атома A, а |
ψ |
2 |
– волновая функ- |
||
1 |
|
|
|||||
ция в 1s-состоянии атома B водорода. Если атомы A и B отстоят далеко друг от друга, то тогда можно считать, что один электрон находится у одного протона, а другой – у другого. По-
скольку при этом вероятность нахождения одного электрона у протона A не зависит от веро- |
|||||
ятности нахождения второго электрона у протона B, то такое состояние можно описать |
|||||
волновой функциейψ |
A ( ) |
B( ) |
|
|
|
1 ψ |
2 . Но оно в силу эквивалентности электронов может быть |
||||
представлено и другой функциейψ |
A ( |
2 ψ |
1 (электроны поменялись местами). Обе функции, |
||
|
|
|
) |
B ( ) |
|
согласно принципа тождественных частиц, отвечают одному и тому же состоянию. В таком случае, исходя из принципа суперпозиции, решение (1.3) является линейная комбинация этих функций
1.4
При этом оказывается, что в зависимости от ориентации спинов обоих электронов коэффициенты c1 и c2 имеют различные значения. Так в случае антипараллельной ориентации спинов
c1 |
= c2 |
= |
1 |
|
|
|
+ 2S |
, |
1.5 |
||||
а в случае параллельной ориентации |
|
2 |
||||
|
|
|
|
|
||
c1 |
= −c2 = |
1 |
|
|
||
2 + 2S |
, |
1.6 |
||||
|
|
|
||||
где S = ∫ψA (1)ψB (1)dv – интеграл перекрытия волновых функций атомов водорода в 1s-
состоянии. Таким образом, возможны два состояния молекулы водорода, которым соответствуют симметричная и антисимметричная волновые функции:
ψ |
|
= |
1 |
ψ |
|
(1)ψ |
|
(2)+ ψ |
|
(2)ψ |
|
(1) |
|
|||||||
и |
s |
2 |
+ 2S |
{ |
A |
|
|
B |
|
|
|
|
A |
|
|
|
|
B |
} |
1.7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ψ |
a |
= |
1 |
ψ |
|
1 |
ψ |
B ( |
2 |
) |
− ψ |
A ( |
2 |
) |
ψ |
|
1 |
|
||
|
2 |
+ 2S |
{ |
A ( ) |
|
|
|
|
|
B ( )} |
1.8 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
и которым соответствуют энергии Es и E a
Рассмотрим теперь, как пространственно распределены электроны в молекуле H2 . Вероятность нахождения электронов в данной части объема молекулы, плотность электронного облака, согласно (1.7) и (1.8), определяется величинами:
|
|
|
|
|
|
|
|
|
|
ψs2 = c12 {ψ12 + ψ22 + 2ψ1ψ2 } |
1.9 |
||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ψa2 |
= c12 {ψ12 |
+ ψ22 − 2ψ1ψ2 } , |
1.10 |
||||
где ψ |
1 |
= ψ |
A ( ) |
ψ |
B ( |
2 |
) |
и ψ |
2 |
= ψ |
A ( |
2 |
) |
ψ |
B ( ) |
|
|
|
1 |
|
|
|
|
|
1 |
. Из (1.9) и (1.10) следует, что при взаимодейст- |
|||||||||
вии двух атомов водорода электронная плотность либо увеличивается, либо уменьшается на величину 2ψ1ψ2 по сравнению с ψ12 + ψ22 . Значение 2ψ1ψ2 наибольшее в пространстве между ядрами (протонами) молекулы H2. Таким образом, в случае симметричной волновой функции ψs плотность электронного облака в области между протонами H2 увеличена, что приводит к образованию эффективного отрицательного заряда электронного облака сосредо-
5
точенного в центре между протонами, создавая, тем самым, достаточно прочную связь между атомами водорода в молекулу H2. В связи с этим симметричную волновую функцию ψs , описывающую электронное облако из двух электронов с антипараллельнонаправленными спинами, называют связывающей молекулярной орбиталью. В случае антисимметричной волновой функции ψa плотность электронного облака между протонами H2 уменьшена, что
5 |
|
|
4 |
6 |
1 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
|
||
|
|
|
|
|
2 |
|
1 |
2 |
5 |
|
|||
|
|
|
||||
|
|
|
|
|
|
|
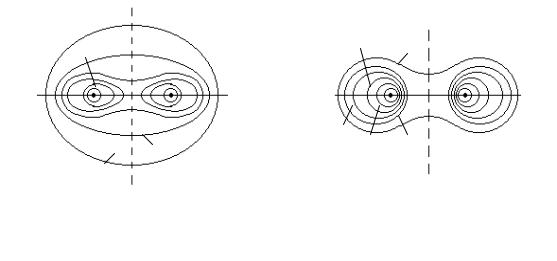
Рис.2 Распределение ψs2 - |
Рис.3 Распределение ψa2 - |
|||||
электронной плотности в |
электорнной плотности в |
|||||
молекуле H2 для случая |
молекуле H2 для случая |
|||||
связи. |
|
отталкивания. |
||||
приводит к образованию двух эффективных отрицательных зарядов, один из которых сосредоточен слева протона A, а другой справа от протона B. Такое расположение зарядов приводит к отталкиванию атомов водорода и поэтому антисимметричную волновую функцию ψa , описывающую электронное облако из двух электронов с параллельными спинами, называют разрыхляющей молекулярной орбиталью. Значения ψ2s и ψ2a , т.е. распределение электронной плотности в молекуле H2 показаны на рис.2 и 3 в виде линий, соединяющих точки равной плотности – равных значений ψ2 . Причем большая цифра у линии означает большую плотность, большую вероятность нахождения электрона.
Вышеизложенный метод Гайтлера и Лондона рассмотрения молекулы H2 , распространенный на другие молекулы, получил название метода валентных связей (ВС). В методе ВС, исходя из экспериментального факта, что для многих молекул различные связи между соседними атомами оказываются независимыми от других атомов, молекулярная волновая функция сложной молекулы строится по аналогии с волновой функцией молекулы водорода в методе Гайтлера и Лондона. Для каждой i–й связи записывается функция вида
ψi = ψAi (j)ψBi (k)+ ψAi |
(k)ψBi (j) |
1.11 |
|
|
|
где j,k – валентные электроны A и B атомов, а ψA i (j) |
и ψBi (k) – волновые функции этих |
|
электронов в атомах A и B , число связей i в молекуле числено равно половине валентных электронов входящих в нее атомов. Полная волновая функция, отвечающая данному состоянию сложной молекулы, представляет собой линейную комбинацию функций (1.11)
Метод ВС дает возможность осуществить количественный (приближенный) расчет связей, причем достигается вполне удовлетворительное согласие наблюдаемой энергии диссоциации молекул с предсказуемым им числом связей. Кроме того, метод ВС позволяет убедительно истолковывать ряд важных особенностей валентности и валентной связи (целочисленность, насыщенность, направленность и др.). Однако в ряде случаев выводы метода ВС приводят к серьезным противоречиям с опытом. Метод ВС неприменим к соединениям, содержащим некомпенсированные электроны. В частности, согласно методу ВС, двухатомные молекулы не должны обладать магнитным моментом, т.е. должны быть диамагнитны (так как все электроны в молекуле спарены). Однако из опыта известно, что молекулы O2 и B2 парамагнитны, т.е. обладают магнитным моментом.
6
