
Книга по математике для поступающих в ВУЗы. КУРС СРЕДНЕЙ И СТАРШЕЙ ШКОЛЫ. Автор- Зайцев Артём Сергеевич
.pdf
ТЕМА 5. ПЛОЩАДЬ ТРЕУГОЛЬНИКА. Понятие площади.
Площадь — это численная характеристика двумерной геометрической фигуры, показывающая размер этой фигуры. Исторически вычисление площади называлось квадратурой. Фигура, имеющая площадь, называется квадрируемой.
! Площадь треугольника равна произведению половины основания на высоту.
ТЕМА 6. ОКРУЖНОСТЬ И КРУГ. КАСАТЕЛЬНАЯ КРУГА.
Геометрическим местом точек называют фигуру, которая состоит из всех точек плоскости, которые имеют определенные свойства.
Кругом называется геометрическое место точек плоскости, равноудаленных от данной точки, которая называется центром круга.
А |
В |
Радиус (R, r) – это расстояние от точки окружности до его центра. |
||
|
|
Хорда – это отрезок, который соединяет две точки окружности. |
||
|
|
Диаметр (D, d) – хорда, проходящая через центр окружности. |
||
|
о |
D = 2 ∙ R; R = |
|
. |
|
|
|||
|
|
На рис.1: О – центр окружности; АС – диаметр; ВС – хорда; АО, СО, ВО – |
||
|
радиусы. |
|
С |
рис. 1 |
Равные хорды окружности равноудалены от центра и имеют одинаковую длину. |

Диаметр окружности, который проходит через середину хорды (отличной от диаметра) пер-
пендикулярен ей. |
|
А |
Круг – это геометрическое место точек плоскости, расстояние от которых |
|
до заданной точки, называемой центром круга, не превышает заданного неотри- |
|
цательного числа, называемого радиусом этого круга. Если радиус равен нулю, |
О |
то круг вырождается в точку; иначе говоря, конечная часть плоскости, ограни- |
|
ченная окружностью. |
рис.2 |
На рис.2: О – центр окружности, АО – радиус. |
|
Касательная круга и ее свойства |
|
Прямую, которая проходит через точку круга перпендикулярно радиусу, |
Апроведенного к данной точке, называют касательной круга. При этом данную
точку называют точкой касания.
 М Касательная круга имеет с ним только одну общую точку – точку касания. О Касание окружностей называется внешним касанием, если центры окруж-
М Касательная круга имеет с ним только одну общую точку – точку касания. О Касание окружностей называется внешним касанием, если центры окруж-
ностей лежат по разные стороны от их общей касательной.
ВНа рисунке: О – центр круга, АВ – касательная.
ТЕМА 7. ВПИСАННЫЕ УГЛЫ.
Центральным углом окружности называют угол с вершиной в его |
|
центре, со сторонами, созданными двумя радиусами. |
А |
Угол АОВ – центральный угол. Часть круга, размещённая в середине |
О |
центрального угла, называют дугой круга, которая соответствует данному |
|
центральному углу. Дуга (выделена) – АВ (часть круга). |
|
Градусной мерой дуги круга называется градусная мера соответствен- |
В |
ного центрального круга. |
|
Вписанным углом называется угол, вершина которого лежит на кругу, |
В |
а стороны пересекают его. |
А |
Угол АВС – вписанный. |
|
Дуга круга, которая лежит в середине вписанного угла, называется ду- |
О |
гой, которая соответствует данному вписанному углу. Дуга – АС (выделена). |
|
! Т Е О Р Е М А : |
С |
Вписанный угол измеряется половиной дуги, на которую он опирается (равен половине цен-
трального угла, который опирается на эту же дугу).
ТЕМА 8. ДЛИНА КРУГА И ПЛОЩАДЬ КРУГА.
Длина l круга вычисляется по формуле:
где R – радиус круга, d – его диаметр.
Длину дуги круга радиуса R можно вычислить по формуле (no – градусная мера дуги):
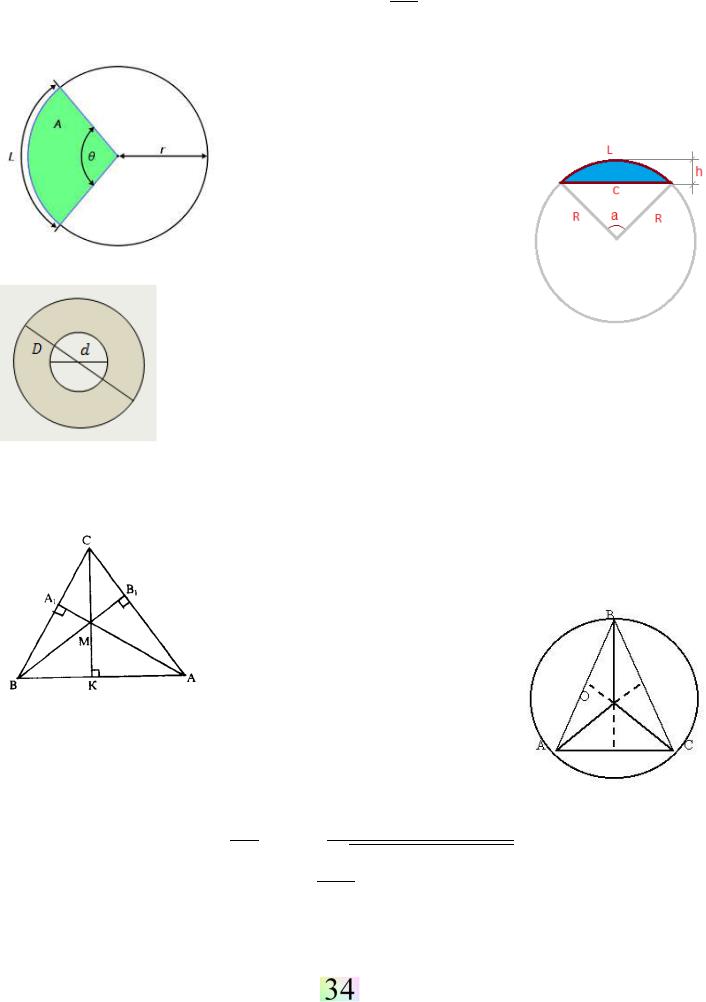
Площадь круга вычисляется по формуле:
где R – радиус круга, d – диаметр.
Круговым сектором называется часть круга, которая лежит в середине соответственного центрального угла.
← Площадь сектора вычисляется по формуле: |
|
, |
|
||
где no – градусная мера. |
|
|
Круговым сегментом называется |
|
|
общая часть круга и полуплоскости. → |
|
|
Если круг пересечь прямой, он де- |
|
|
лится на два круговых сегмента. |
|
|
Площадь кругового сегмента: |
|
|
. |
|
|
Круговое кольцо – это часть плоскости, ограниченная двумя окружностями с разными радиусами.
Площадь кругового кольца равна разнице площадей внешнего и внут-
реннего кругов. |
|
|
, где D – диаметр внешнего круга, а d – диа- |
|
|||
метр внутреннего круга. |
|
||
ТЕМА 9-10. ВПИСАННЫЕ И ОПИСАННЫЕ ТРЕУГОЛЬНИКИ.
Серединным перпендикуляром называется прямая, перпендикулярная стороне треугольника и делящая её пополам. На рисунке слева CK, BB1, AA1 – серединные перпендикуляры.
Окружность называется описанной вокруг треугольника, если она проходит через все его вершины. Треугольник при этом является вписанным.
Центр окружности, описанного вокруг треугольника, является точкой пересечения серединных перпендикуляров к сторонам треугольника.
Вокруг любого треугольника можно описать окружность, причем только одну.
Радиус R описанной окружности можно вычислить по формуле:
|
|
√ |
где |
– длины сторон треугольника, |
– полупериметр треугольника, – площадь тре- |
угольника.
Радиус окружности описанной вокруг равностороннего треугольника можно вычислить по
формуле: |
|
|
|
√ |
|
, где а – сторона треугольника. |
|
|
|
|
|
|
|||
√ |
|||||||
|
|
|
|||||

Радиус окружности, описанной вокруг прямоугольного треугольника можно вычислить по
|
√ |
формуле: |
где a, b – длины катетов прямоугольного треугольника, c – гипотенуза. |
Окружность называется вписанной в треугольник, если она касается всех его сторон. Треугольник при этом называется описанным вокруг окружности.
Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.
В любой треугольник можно вписать круг, причем только один.
Радиус r вписанной в треугольник окружности ра-
вен: |
|
|
|
|
|
|
|
|
|
√ |
|
|
a, b, c – длины сторон треугольника, S – площадь тре- |
||
|
|
|
|
|
|
||||||||||
угольника, p – полупериметр. |
|||||||||||||||
|
Радиус r окружности, вписанной в равносторонний треугольник, можно вычислить по форму- |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ле: |
|
|
|
|
|
|
|
|
|
√ |
, |
где a – длина стороны треугольника, R – радиус окружности, описанной |
|||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
√ |
|
|
|||||||
вокруг треугольника.
Радиус r окружности, вписанной в прямоугольный треугольник, можно вычислить по форм.:
где a,b – длины катетов, c – длина гипотенузы.
ТЕМА 11. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ОСТРОГО УГЛА ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА.
Синусом острого угла прямоугольного тре-
угольника называют отношение катета, противолежащего углу , к гипотенузе.
Косинусом острого угла прямоугольного тре-
угольника называют отношение катета, прилежащего к углу , к гипотенузе.
Тангенсом острого угла прямоугольного тре-
угольника называют отношение катета, противолежащего углу , к катету, прилежащего к углу .
Котангенсом острого угла прямоугольного треугольника называют отношение катета, прилежаще-
го к углу , к катету, противолежащего углу .
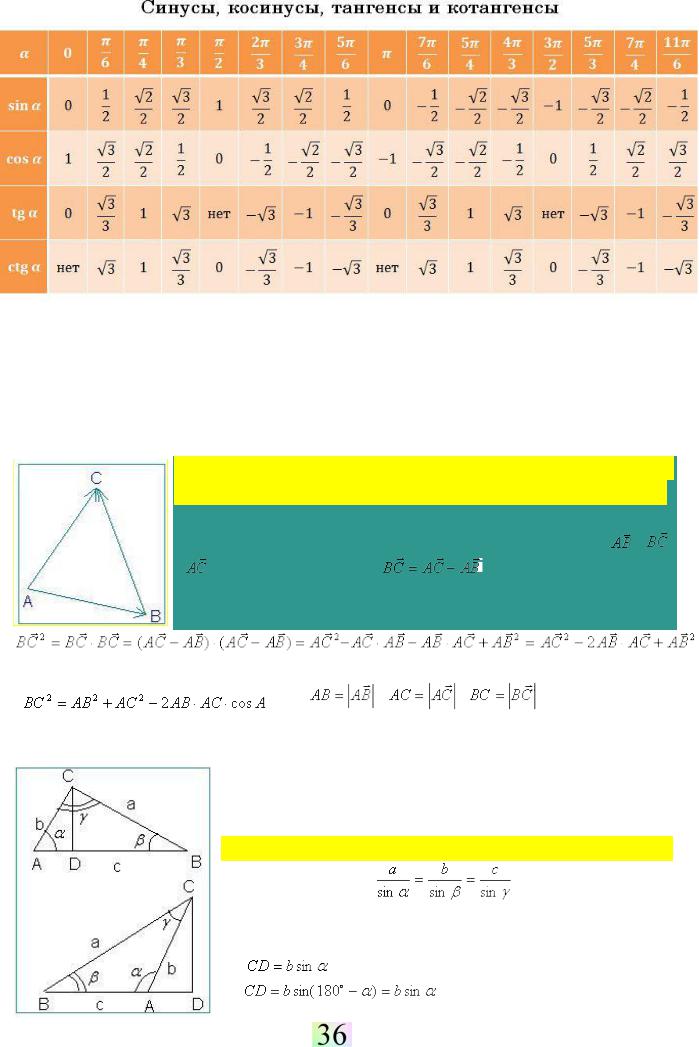
Основные тригонометрические тождества (доп. материал см. тему 17, алгебра):
! При увеличении острого угла синус и тангенс угла возрастают, а косинус и котангенс - убы-
вают.
ТЕМА 12. ТЕОРЕМА КОСИНУСОВ И СИНУСОВ.
Теорема косинусов. Квадрат любой стороны треугольника
равен сумме квадратов двух других сторон без удвоенного про-
|
|
изведения этих сторон на косинус угла между ними. |
. |
|
|
|
|||||||
|
|
|
Доказательство. Дан ∆АВС. Рассмотрим векторы |
, |
|
|
|
|
|
||||
|
|
, |
(рис. 13). Очевидно , |
. Возведем это равенст- . |
|
|
|||||||
|
|
во скалярно в квадрат: |
|
|
. |
|
|
||||||
|
|
. . |
. |
|
|
|
. |
|
|
||||
|
Используя теперь определение скалярного произведения векторов, имеем |
. |
|||||||||||
|
|||||||||||||
|
|
|
|
, где |
, |
, |
– длины сторон . |
|
|
||||
|
∆АВС, <A – угол между сторонами АВ и АС. Теорема доказана. |
|
. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
. |
|
|
|
||
|
|
|
|
Теорема синусов. Стороны треугольника пропорци- |
|
|
|
|
|||||
|
|
|
|
ональны синусам противолежащих углов. |
|
. |
|
|
|||||
|
|
|
|
Доказательство. Рассмотрим ∆АВС со сторонами - |
|
|
|
||||||
|
|
|
|
a, b, c и противолежащими углами α, β, γ. Докажем, что . |
|
||||||||
|
|
|
|
|
|
|
|
. |
|
|
|||
|
|
|
|
Из вершины С треугольника АВС опусти высоту CD. |
|
||||||||
|
|
|
|
Из прямоугольного ∆АСD, если α – острый угол, получа- |
|
|
|
||||||
|
|
|
|
ем |
. Если α– тупой угол, |
|
. |
|
|
||||
|
|
|
|
то |
|
|
|
. |
|
|
|||
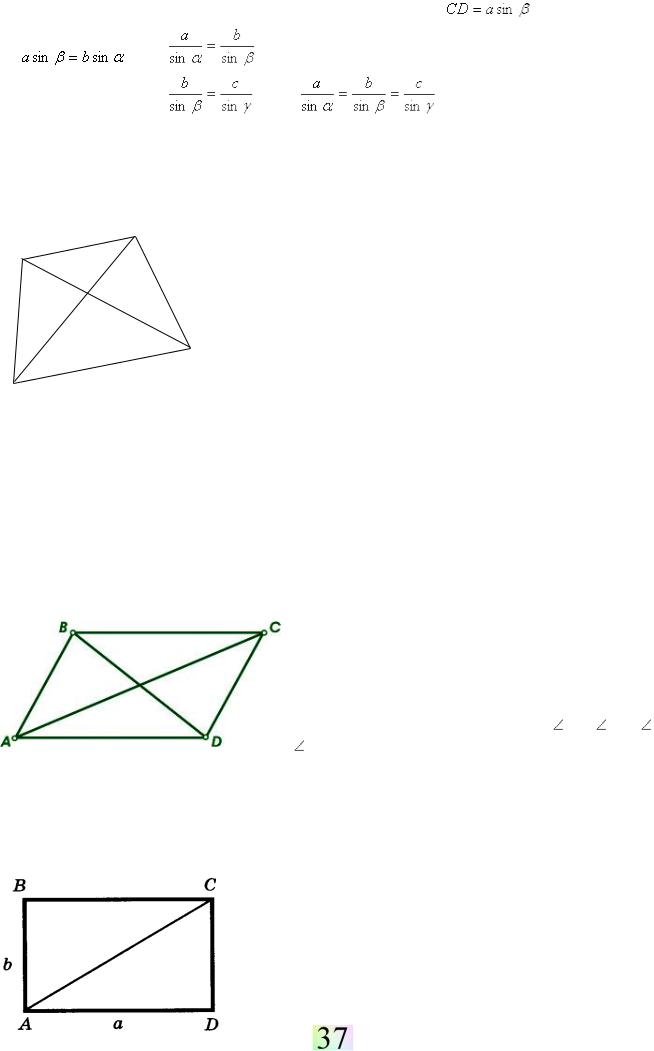
Аналогично из прямоугольного ∆BCD получаем: |
.Таким образом, , |
|
, т.е. |
. Опуская высоту в треугольнике АВС из вершины А, |
|
аналогично имеем |
. так, |
-. |
ТЕМА 13. ЧЕТЫРЕХУГОЛЬНИКИ: ПАРАЛЛЕЛОГРАММ, ПРЯМОУГОЛЬНИК, РОМБ, КВАДРАТ, ТРАПЕЦИЯ.
K |
|
Четырехугольником называется фигура, состоящая из четырех |
M |
точек и четырех отрезков, которые последовательно их соединяют. При |
|
|
этом ни одна из трех данных точек не должна лежать на одной прямой, а |
|
О |
отрезки, которые их соединяют, не должны пересекаться. |
|
|
|
Данные точки называются вершинами четырехугольника, а от- |
|
|
резки, которые их соединяют, – сторонами четырехугольника. |
|
C |
Вершины четырехугольника называются соседними, если они яв- |
P |
|
ляются концами одной из его сторон. Несоседние вершины называются |
|
|
противолежащими. |
MKCP – четырехугольник; |
|
Отрезки, соединяющие противолежащие вершины четырехуголь- |
вершины M и P – соседние; ника, называются диагоналями. |
||
P и K – противолежащие; |
|
Стороны четырехугольника, исходящие из одной вершины, назы- |
отрезки MC, PK – диагонали; |
ваются соседними. |
|
стороны MK и KC – соседние; |
Стороны, не имеющие общих вершин, называются противолежа- |
|
MK и PC – противолежащие. |
щими. |
|
P = MK + KC + CP + PM |
|
Сумма длин всех сторон четырехугольника называется перимет- |
|
|
ром. |
Параллелограмм
|
Параллелограмм – это четырехугольник, у которо- |
го противолежащие стороны попарно параллельны. |
|
|
Свойства параллелограмма: |
1. |
Противолежащие стороны равны (AB = CD, AD = |
BC). |
|
2. |
Противолежащие углы равны ( A = C, B = |
D). |
|
3.Диагонали точкой пересечения делятся пополам.
4.Каждая диагональ разбивает параллелограмм на два равных треугольника.
5.Сумма углов, прилежащих к одной стороне параллелограмма, равна 180о.
6.! Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
Прямоугольник
Прямоугольником называется параллелограмм, у которого все углы прямые.
Свойства прямоугольника:
Прямоугольник имеет все свойства параллелограмма, кроме того, диагонали прямоугольника равны.
Диагонали и углы у прямоугольника равны.
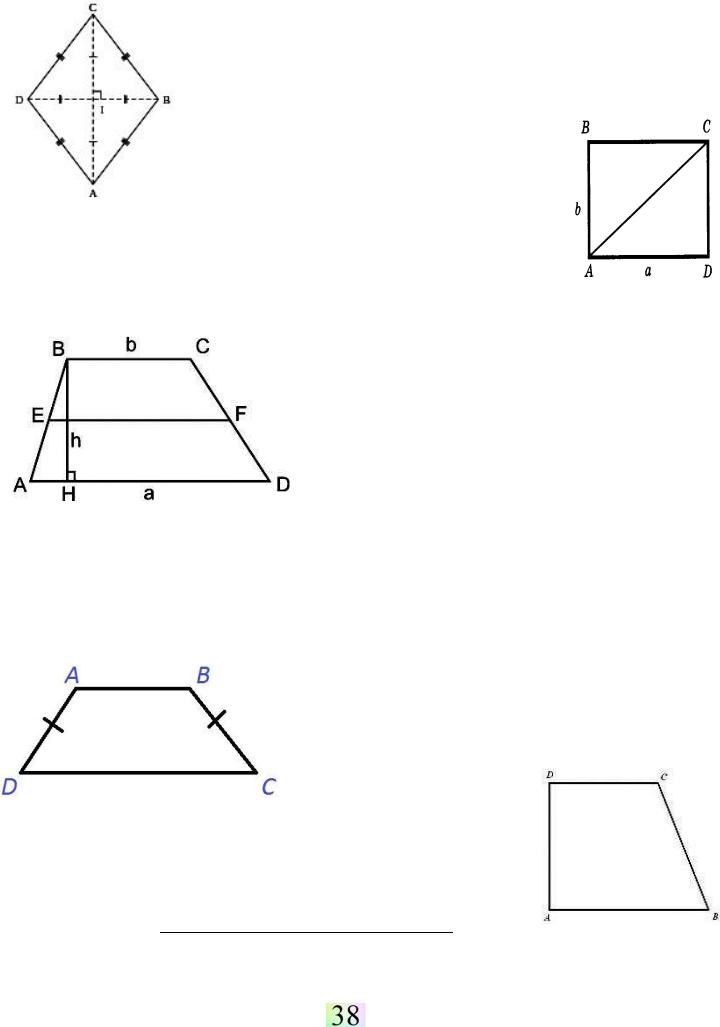
Ромб
← Ромб – параллелограмм, у которого все стороны равны.
Свойства ромба:
1.Диагонали ромба взаимно перпендикулярны.
2.Диагонали ромба являются биссектрисами его углов.
Квадрат
Квадрат – прямоугольник, у которого все стороны равны; ромб, у которого все углы прямые. →
Свойства квадрата:
Квадрат имеет все св-ва прямоугольника и ромба.
1.У квадрата все углы прямые и все стороны равны.
2.Диагонали квадрата равны и пересекаются под прямым углом.
3.Диагонали квадрата являются биссектрисами его углов. Каждая диагональ квадрата создает со стороной угол 45о.
Трапеция
Трапеция – четырехугольник, у которого две стороны параллельны, а две другие – нет.
Параллельные стороны трапеции называются основаниями, а непараллельные стороны – боковыми. На рисунке слева ABCD – трапеция, поскольку AD || BC, а AB || CD, стороны BC и AD – основания трапеции, AB и CD – боковые стороны трапеции.
Высотой трапеции называют перпендикуляр, проведенный из любой точки одного из оснований на прямую, которая содержит второе основание (или это расстояние между основаниями трапеции). На рисунке BH – высота трапеции ABCD.
Средней линией трапеции называют отрезок, которые соединяет середины боковых сторон трапеции. На рисунке EF – средняя линия трапеции ABCD.
Свойства трапеции:
1. Сумма углов трапеции, прилежащих к боковой стороне, равна 180о.
2. ! Средняя линия трапеции параллельна основаниям и равна их полусумме. |
|
. |
|
← Трапеция, у которой боковые стороны равны, называ-
ется равнобокой (равнобедренной) трапецией. Свойства равнобокой трапеции:
1.Углы при основании равны.
2.Диагонали равны.
Прямоугольной называется трапеция, у которой одна из боковых сторон перпендикулярна основаниям. Эта сторона является высотой. →
!! Если в равнобокой трапеции диагонали взаимно перпендикулярны, то её высота равна средней линии:
!Окружность можно описать только вокруг равнобедренной трапеции.
!Если в равнобокую трапецию вписать окружность, то её боковая сторона равна ср. линии.

ТЕМА 14. ПЛОЩАДИ ЧЕТЫРЕХУГОЛЬНИКОВ.
Площадь прямоугольника равна про-
изведению двух его смежных сторон:
Площадь прямоугольника равна по-
ловине квадрата его диагонали, умноженной на синус угла между диагоналями:
Площадь квадрата равна квадрату его стороны:
Площадь квадрата равна половине квадрата его диагонали:
Площадь параллелограмма равна произведению его стороны (основания) на высоту, проведённую к ней:
Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними:
Площадь параллелограмма равна по-
ловине произведения его диагоналей на синус угла между ними:
Площадь ромба равна произведению квадрата его стороны на синус угла ромба:
Площадь ромба равна половине произведения его диагоналей:
Площадь трапеции равна произве-
дению полусуммы оснований на высоту:
Площадь трапеции равна произве-
дению средней линии на высоту:
Если диагонали равнобедренной трапеции взаимно перпендикулярны, то
, где h - высота трапеции.
ТЕМА 15. ЛОМАНАЯ. МНОГОУГОЛЬНИКИ.
Ломаной А1, А2, А3, …, Аn называется фигура, состоящая из точек А1, А2, А3, …, Аn и соединяющих их отрезков А1А2, А2А3, …, Аn-1An. Точки А1, А2, А3, …, Аn называются вершинами ломаной, а отрезки А1А2, А2А3, …, Аn-1An – звеньями ломаной. Ломаная называется простой, если она не имеет самопересечений.
Ломаная называется замкнутой, если у неё концы совпадают. Длиной ломаной называется сумма длин её звеньев.
Длина ломаной не меньше длины отрезка, соединяющего её концы.
Выпуклые многоугольники
Простая замкнутая ломаная называется многоугольником, если её соседние звенья не лежат на одной прямой. Вершины ломаной называется вершинами многоугольника, а звенья ломаной - сто-
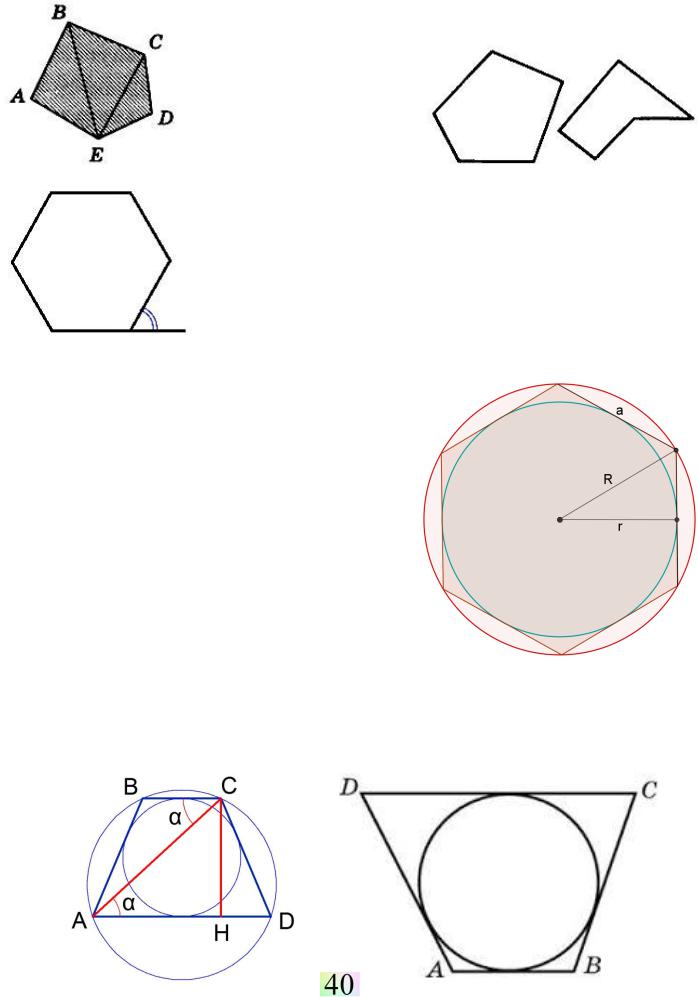
ронами многоугольника. Отрезки, соединяющие несоседние вершины многоугольника, называются диагоналями. Многоугольник с n-вершинами, т.е. с n-сторонами, называется n-угольником.
← Плоским многоугольником, или многоугольной областью, назы-
вается конечная часть плоскости, ограниченная многоугольником. Многоугольник называ-
ется выпуклым (→), если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону. При этом сама прямая считается
принадлежащей полуплоскости.
Углом выпуклого многоугольника при данной вершине называет-
ся угол, образованный его сторонами, которые сходятся в этой вершине.
← Внешним углом выпуклого многоугольника при данной вершине называется угол, смежный внутреннему углу многоугольника при этой вершине.
!!Сумма углов выпуклого n-угольника равна 180о ∙ (n – 2).
!Сумма внешних углов выпуклого n-угольника, взятых по одному при каждой вершине, равна 360о.
Многоугольник называется вписанным в окружность, если все его вершины лежат на некоторой окружности, которая, в свою очередь, называется описанной около многоугольника.
Многоугольник называется описанным около окружности, если все его стороны касаются некоторой окружности, которая, в свою очередь, называется вписан-
ной в многоугольник.
!У четырехугольника, описанного около окружности, суммы длин противолежащих сторон равны.
Если в выпуклом четырехугольнике суммы длин противоположных сторон равны между собой, то в него можно вписать окружность.
!Если трапеция вписана в окружность, то она равнобедренная.
Каждый внутренний угол правильного n-угольника равен |
|
, а внешний = |
|
. |
|
|
Апофемой правильного многоугольника называют перпендикуляр, проведенный из центра правильного многоугольника к его стороне (на рисунке выше апофема обозначена r ↑).
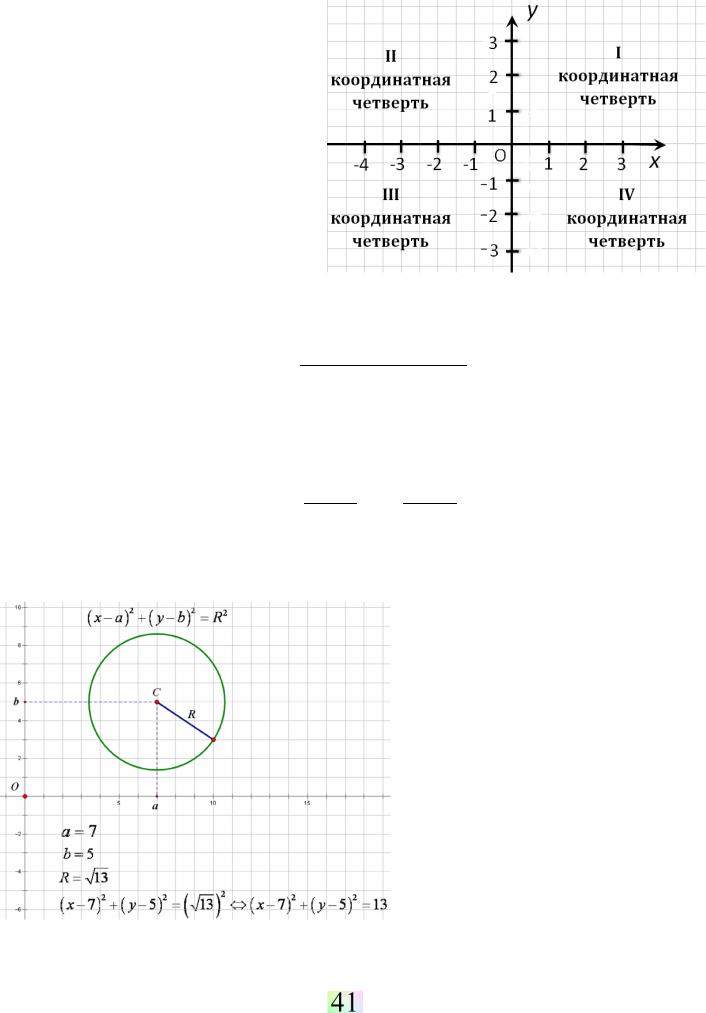
ТЕМА 16. ДЕКАРТОВЫ КООРДИНАТЫ НА ПЛОСКОСТИ.
Декартова система координат на плоскости создается двумя взаимно перпендикулярными осями (ось OX –
ось абсцисс и ось OY – ось ординат),
которые имеют общее начало O (начало координат) и одинаковый масштаб осей.
Каждой точке плоскости по определенному правилу задаётся в соответствии пара чисел - абсцисса и ордината (x; y). Эти числа называются декарто-
выми координатами точки.
Расстояние между двумя точками на плоскости
Расстояние между двумя точками равно квадратному корню из суммы квадратов разницы одноименных координат.
√
где d – расстояние между точкой А1 с координатой (х1; у1) и точкой А2 с координатами (х2; у2).
Координаты середины отрезка
Координаты середины отрезка равны полусумме соответственных координат его концов.
где (х1; у1) и (х2; у2) – координаты начала и конца отрезка.
Уравнение фигуры
Уравнением фигуры в декартовых координатах на плоскости называется уравнение с двумя переменными х и у, которые удовлетворяют координаты любой точки фигуры, и только они.
← Уравнение окружности. Уравнение является уравне-
нием окружности с центром в точке С0 (a; b) и радиусом R.
Если центром является начало координат, то уравнение окружности имеет вид:
.
Уравнение прямой. Любая прямая в декартовых координатах х, у имеет уравнение вида ах + by + c = 0, a, b, c – некоторые числа.
! Условия перпендикулярности двух прямых. Если прямые l и m заданы соответственно уравнениями y = k1x + b1 и y = k2x + b2, то они перпендикулярны тогда, когда k1 ∙ k2 = –1.
