
Книга по математике для поступающих в ВУЗы. КУРС СРЕДНЕЙ И СТАРШЕЙ ШКОЛЫ. Автор- Зайцев Артём Сергеевич
.pdf
Основные свойства логарифмов:
Логарифм числа
Уравнение ах = b, где a > 0, a ≠ 0, b > 0, имеет единственный корень. Его называют логарифмом числа b по основанию а и обозначают loga b.
Логарифмы по основанию 10 называют десятичными и обозначаются lg. 10lgb = b. Логарифмы по основанию e (экспонента = 2,7) называют натуральными и обозначают ln.
Логарифмическая функция y = loga x, a > 0, a ≠ 1
Функцию вида y = loga x, где a > 0, a ≠ 1, называют логарифмической. Основные свойства логарифмической функции:
1. Область определения: (0; + ).
2.Область значений: множество всех действительных чисел R.
3.Если х = 1, то у = 0.
4.Функция y = loga x не является ни парной, ни непарной.
5.Если a > 1, функция y = loga x возрастает, а при 0 < a < 1 – убывает.
6.Если a > 1 и x > 1, то y = loga x > 0. Если a > 1 и 0 < x < 1, то y = loga x < 0. Если 0 < a < 1 и x > 1, то y = loga x < 0. Если 0 < a < 1 и 0 < x < 1, то y = loga x > 0.
7.График функции y = loga x изображён на рисунке ниже.

ТЕМА 24. ПРОИЗВОДНАЯ ФУНКЦИИ. ДИФФЕРЕНЦИРОВАНИЕ.
Производная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке),
называют дифференцируемой (в данной точке). |
|
|
Определение производной функции через предел: |
|
|
Пусть в некоторой окрестности точки |
определена функция |
|
Производной функции в точке называется предел, если он существует, |
||
Общепринятые обозначения производной функции |
в точке |
|
Правила дифференцирования
Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. Если C — постоянное число и f=f(x), g = g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования: Это важно помнить ↓
|
|
|
, где g ≠ 0 |
|
|
|
|
|
|
|
, где g ≠ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция |
|
Производная |
|
|
Примечание |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство |
|
|
|
|
|
Фиксируем |
|
, придадим приращение аргументу . |
|
|
|
|
|
|
|
Вычислим приращение функ- |
|
|
|
|
|
ции: |
, |
||
|
|
|
|
т.о |
|
|
|
|
|
|
|
|
См. |
||
|
|
|
|
|
|
|
|

Доказательство
Фиксируем 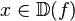 , придадим приращение аргументу
, придадим приращение аргументу 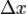 . Вычислим приращение функ-
. Вычислим приращение функ-
ции: 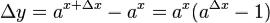 ,
,
т.о 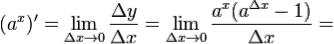 См.
См.
ТЕМА 25. ПЕРВООБРАЗНАЯ, НЕОПРЕДЕЛЁННЫЙ И ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛЫ.
Функцию F (x) называют первообразной для функции f (x) на заданном промежутке, если для всех x из этого промежутка F′ (x) = f (x).
Функция F (x) = x2 является первообразной для функции f (x) = 2x, т.к. F′ (x) = (x2)′ = 2x = f (x).
Основное свойство первообразной:
Если F (x) – первообразная для функции f (x) на заданном промежутке, то функция f (x) имеет множество первообразных, и все эти первообразные можно записать в виде F (x) + C, где С - произвольная постоянная.
Функции F (x) = х2 + C являются первообразными для функции f (x) = 2x, поскольку F′ (x) = (x2 + C)′ = 2x = f (x).

Правила вычисления первообразных
1.Первообразная суммы функции равна сумме первообразных функций: т.е. если F (x) - первообразная для f (x), а G (x) – первообразная для функции f (x) + g (x).
2.Постоянный множитель можно выносить за знак первообразной, т.е. если F (x) – первообразная для функции f (x) и C – постоянная, то CF (x) – первообразная для Cf (x).
3. Если F (x) – первообразная для f (x) и k ≠ 0, b – постоянная, то |
|
– первообразная |
|
||
для функции f (kx + b). |
|
|
Неопределённый интеграл
Неопределённым интегралом от функции f (x) называют выражение F (x) + C, т.е. совокуп-
ность всех первообразных данной функции f (x).
Обозначается так: ∫ , где функцию f (x) называют под интегральной функцией; выражение dx – под интегральное выражение; F (x) – одна из первообразных функции f
(x); С – произвольная постоянная.
Основные правила интегрирования
1. |
∫( |
) |
∫ |
∫ |
. |
|
|
2. |
∫ |
|
∫ |
. |
|
|
|
3. |
Если k ≠ 0 и k, b – постоянные, то ∫ |
|
|
. |
|||
|
|||||||
|
|
|
|
Неопределённые интегралы |
|||
! Определённый интеграл. Пусть задана непре-
рырвная функция y = f (x), определённая на про-
межутке [a; b], тогда определённым интегралом
от числа a до b функции f (x) называют прирощение первообразной F (x) этой функции, т.е.
∫ Числа a и b называют соответственно нижним и верхним пределами интегрирования.

ТЕМА 26. ПРИМЕНЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА.
Площадь S криволинейной трапеции
(фигура, ограниченная графиком непрерывной положительной на промежутке [a; b] функции f (x), осью Ох и прямыми х = а, х = b) вычисля-
ется по формуле |
∫ |
. |
Площадь фигуры
Если на заданном промежутке [a; b] непрерырвные функции y = f (x) и y = g (x) имеют свойственность f (x) ≥ g (x) для всех
x [a; b], то |
∫ ( |
) . |
ТЕМА 27. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ. ТРЕУГОЛЬНИК ПАСКАЛЯ.
Перестановки (без повторений)
Любое упорядоченное множество, которое состоит из n элементов, называется перестановкой из n элементов.
Число перестановок из n элементов (обозначается Pn) равен произведению всех натуральных чисел от 1 до n, то есть n! (читается: «эн факториал»).
Pn = 1 ∙ 2 ∙ 3 ∙ … ∙ n = n!
По определению 0! = 1.
Таблица факториалов чисел от 1 до 10
n |
1 |
2 |
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
n! |
1 |
2 |
|
6 |
24 |
120 |
720 |
5 040 |
40 320 |
362 880 |
3 628 800 |
||
|
|
|
|
|
Размещения (без повторений) n |
|
|
||||||
|
Любое упорядоченное множество из m элементов данного множества, которое содержит n |
||||||||||||
элементов, где m ≤ n, называется размещением из n элементов по m элементов. |
|
||||||||||||
|
Число размещений из n элементов по m обозначают . |
|
|
|
|
||||||||
|
Число размещений из n элементов по m равняется произведению m последовательных нату- |
||||||||||||
ральных чисел, наибольшим из которых является n: |
|
|
|
. |
|
|
|||||||
|
|
|
|
|
|||||||||
|
Если n = m, то |
|
. |
|
|
|
|
|
|
|
|
||
Комбинации (без повторений)
Любое множество из m элементов данного множества, которое содержит n элементов, называется комбинацией из n элементов по m элементов.

Число комбинаций из n элементов по m обозначают символом .
Число комбинаций из n элементов по m (1≤ m ≤ n) равно дроби, числителем которой является произведение m последовательных натуральных чисел, наибольшим из которых является n, а знаме-
нателем – произведение m первых последовательных натуральных чисел: |
|
. |
|||
|
|||||
|
|
|
Свойства комбинаций |
|
|
1) |
. |
|
|
||
2) |
|
|
. |
|
|
|
|
|
|||
3) |
. |
|
|
||
4) |
|
|
, то есть число всех подмножеств для множества, которое состоит |
||
|
из m элементов, равно 2m. |
|
|
||
Треугольник Паскаля
Все возможные значения (n = 0, 1, 2, …, m = 0, 1, 2, …,) можно записать в виде треугольной таблицы. Такая таблица называется треугольником Паскаля.

ГЕОМЕТРИЯ
ТЕМА 1. ПРОСТЕЙШИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ИХ СВОЙСТВА.
Аксиомы планиметрии
Основными фигурами планиметрии являются точка и прямая.
Аксиомы принадлежности точек и прямых на плоскости:
1.Какой бы ни была прямая, существуют точки, ей принадлежащие и ей не принадлежащие.
2.Через две точки можно провести прямую, и только одну.
Аксиомы взаимного размещения точек на прямой и на плоскости:
1.Из трех точек на прямой одна и только одна лежит между двумя другими.
2.Прямая разбивает плоскость на две полуплоскости.
3.Отрезок MN пересекает прямую a, если точки M и N лежат в разных полуплоскостях относительно прямой a.
Аксиомы измерения отрезков и углов:
1.Каждый отрезок имеет определенную длину, больше нуля. Длина отрезка равна сумме длин частей, на которые разбивается отрезок любой своей точкой.
Расстояние между двумя точками – это длина отрезка, соединяющего эти точки.
2.Каждый угол имеет определенную градусную меру, больше нуля. Развернутый угол равен 180о. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
Аксиомы отложения отрезков и углов:
1.На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины, и только один.
2.От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньше 180о, и только один.
3.Каким бы ни был треугольник, существует равный ему треугольник в заданном размещении относительно данной полупрямой.
Углы
Углом называется фигура, образованная двумя разными полупрямыми, исходящими из одной точки (рис.1).
Биссектрисой называется луч, проходящий между сторонами угла и делящий угол на две равные части (рис.2). рис.1 рис.2
Виды углов:
прямой (90о); |
тупой (больше 90о); |
острый (меньше 90о); |
развернутый (180о). |
Аксиома параллельных прямых: через точку, не лежащую на данной прямой, можно провести на плоскости прямую, параллельную данной, и только одну.
Смежные и вертикальные углы:
смежными углами называются углы, у которых одна сторона общая, а две другие стороны этих углов являются дополняющими полупрямыми. Сумма смежных углов равна 180о (если два угла равны, то смежные с ними углы тоже равны; угол, смежный с прямым углом, является прямым).
вертикальными называются углы, в которых стороны являются дополняющими полупря-
мыми. Вертикальные углы равны.

Параллельные и перпендикулярные прямые: |
|
|
|
|
|
|||
Две прямые на плоскости называются параллельными, |
a |
|
|
|
||||
если они не пересекаются. а||b |
|
b |
|
|
|
|||
Две прямые называются перпендикулярными, если |
|
|
|
|
|
|||
|
b |
|
|
|
||||
они пересекаются под прямым углом. Через данную точку |
|
|
|
|
|
|||
можно провести прямую, перпендикулярную данной, и толь- |
|
|
|
|
||||
ко одну. а | b |
|
a |
|
|
|
|||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
Углы при пересечении двух прямых секущей: |
|
|
|
|
|
|||
|
|
|
|
|
||||
При пересечении двух прямых третьей, секущей, |
|
|
|
|
|
|||
образуются (a и b могут быть и не параллельны): |
|
a |
|
2 3 |
||||
а) внутренние односторонние: 1 и 8, 4 и 5; |
|
|
1 4 |
|
||||
б) внутренние разносторонние: 1 и 5, 4 и 8; |
|
|
|
|
|
|||
в) соответственные: 1 и 7, 4 и 6, 2 и 8, 3 и 5. |
b |
|
8 5 |
|
||||
|
|
|
|
|
7 |
6 |
|
|
Признаки параллельности прямых:
1. Две прямые параллельны, если: а) внутренние разносторонние углы равны; б) соответственные углы равны;
в) сумма внутренних односторонних углов равна 180о.
2.Две прямые, перпендикулярные третьей прямой, параллельны.
3.Две прямые, параллельные третьей, параллельны друг другу.
Свойства углов, образованных при пересечении параллельных прямых секущей:
1. Если две прямые параллельны, то: а) внутренние разносторонние углы равны; б) соответственные углы равны;
в) внутренние односторонние углы в сумме равны 180о.
2.Если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и второй параллельной прямой.
3.Если две пересекающиеся прямые соответственно параллельны двум перпендикулярным прямым, то они перпендикулярны.
ТЕМА 2. ТРЕУГОЛЬНИКИ. ВИДЫ ТРЕУГОЛЬНИКОВ.
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
Биссектрисой треугольника называется отрезок, который соединяет вершину угла и точку противолежащей стороны и делит угол пополам. Свойство: Биссектриса делит противолежащую сторону на части, пропорциональные к прилежащим сторонам.
! ВСЕ биссектрисы треугольника пересекаются в одной точке, которая является центром круга, вписанного в треугольник.
Высотой треугольника называется перпендикуляр, опущенный из его вершины к прямой, содержащей противолежащую сторону треугольника.
Средняя линия треугольника – отрезок, соединяющий середины двух его сторон. Треугольники называются равными, если равны их соответственные элементы: стороны, уг-
лы, медианы, биссектрисы, высоты.
Признаки равенства треугольников:
Первый признак равенства треугольников – по двум сторонам и углу между ними.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Второй признак равенства треугольников – по стороне и прилежащей к ней углам.
Если сторона и два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Третий признак равенства треугольников – по трем сторонам.
Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.
Виды треугольников:
равнобедренный (равны две боковые стороны); равносторонний (все стороны равны); В прямоугольный (один угол – прямой).
-Свойства равнобедренного треугольника:
1.У равнобедренного треугольника две равные стороны (боковые).
2. У равнобедренного треугольника углы при основании равны.
3. У равнобедренного треугольника медиана, проведенная к основанию, является биссектрисой и высотой.
А |
К |
С |
Признаки равнобедренного треугольника:
1.Если в треугольнике два угла равны, то он равнобедренный.
2.Треугольник является равнобедренным, если в нем совпадают: а) высота и медиана; б) или высота и биссектриса;
в) или медиана и биссектриса.
ВЫВОД: в равнобедренном треугольнике высота, медиана и биссектриса, проведенные к ос-
нованию, совпадают. |
B |
|
|
- Свойства равностороннего треугольника: |
|
1. |
У равностороннего треугольника все углы равны. |
K |
2. |
Любая медиана равностороннего треугольника яв- |
|
ляется биссектрисой и высотой. |
|
|
|
АK – медиана, высота, биссектриса. |
|
|
A |
C |
Треугольник ABK – прямоугольный, в котором AK и BK – катеты, AB – гипотенуза.
– Признаки равенства прямоугольных треугольников:
Первый признак: по двум катетам. Если два катета одного прямоуг. треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.
Второй признак: по гипотенузе и катету. Если гипотенуза и катет одного прямоугольного треугольника соответственно гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
Третий признак: по гипотенузе и острому углу. Если гипотенуза и острый угол одного пря-
моугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Четвертый признак: по катету и острому углу. Если катет и острый угол одного прямо-
угольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.

!В прямоугольном треугольнике против угла 30о лежит катет, равный половине гипотенузы.
!Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.
ТЕМА 3. СУММА УГЛОВ ТРЕУГОЛЬНИКА.
1.Сумма углов треугольника равна 180о.
2.В любом треугольнике два угла – острые.
3.Если один из углов равнобедренного треугольника равен 60о, то этот треугольник – равносторонний, т.е. у равностороннего треугольника все углы равны 60о.
В |
|
Внешним углом треугольника при данной вершине |
|
|
называется угол, смежный с углом треугольника при этой |
|
|
вершине. |
|
|
Внешний угол треугольника равен сумме двух внут- |
|
|
ренних углов, не смежных с ним (т.к. сумма смежных углов |
|
|
= 180о и сумма углов треугольника = 180о). |
А |
С |
Центр окружности, вписанной в равнобедренный |
|
|
треугольник, принадлежит медиане, высоте и биссектри- |
|
|
се, проведенным с вершины к основанию. |
Центры окружности, описанной около равностороннего треугольника, и окружности, вписанной в него, совпадают. Это точка пересечения медиан, биссектрис и высот равностороннего треугольника.
ТЕМА 4. ПОДОБИЕ ТРЕУГОЛЬНИКОВ. ТЕОРЕМА ПИФАГОРА.
Признаки подобия треугольников
Первый признак подобия треугольников (по двум углам).
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники являются подобными.
Второй признак подобия треугольников (по двум сторонам и углу между ними).
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, созданные этими сторонами, равны, то такие треугольники являются подобными.
Третий признак подобия треугольников (по трем сторонам).
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники являются подобными.
|
|
|
Теорема Пифагора. |
А |
|
Сумма квадратов катетов равна квадрату гипотенузы. |
|
|
|
|
На рисунке 4.1: AB – гипотенуза, CB и AC – катеты прямоуг.тр-ка. |
|
|
c |
• AC2 + CB2 = AB2; |
b |
|
• a2 = c2 – b2; |
|
|
|
|
• b2 = c2 – a2. |
|
a |
|
|
|
|
|
|
С |
В |
||
|
|
Рисунок 4.1 |
|
