Завдання №5

Однією з важливих тем в математиці є тема дії з дробами. Дроби в нашому житті зустрічаються майже кожен день, як у побуті так і в роботі, тому в математиці дробам приділяють велику увагу. Для виконання наступного завдання потрібно насамперед знання правил обрахування та уважність. Дії з дробами –це доволі кропітка робота, яка не допускає ніяких наближень та припущень бо вони можуть привести до невірної відповіді. Нижче буде приведено основні правила дій з дробами та деякі приклади застосування тих чи інших правил.

Дії над дробами

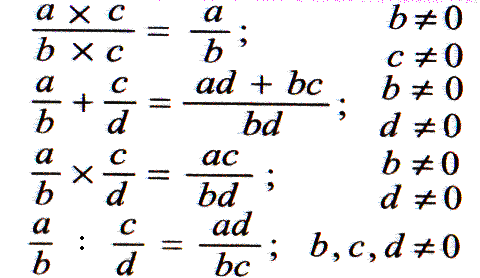
При додаванні (відніманні) дробів з однаковими знаменниками до чисельника першого дробу додають чисельник другого дробу (від чисельника першого дробу віднімають чисельник другого дробу) і залишають той же знаменник. Отриманий дріб, якщо це можливо, скорочують. Наприклад, ,.

При додаванні (відніманні) дробів з різними знаменниками переважніше попередньо звести їх до найменшого спільного знаменника. Наприклад, .

При додаванні мішаних дробів потрібно додати окремо цілі частини і дробові частини. Наприклад,

.

При відніманні мішаних дробів варто розрізняти такі випадки:

a) дробова частина зменшуваного більше або дорівнює дробовій частині від’ємника; у цьому випадку від цілої частини зменшуваного віднімають цілу частину від’ємника, а від дробової частини зменшуваного – дробову частину від’ємника. Наприклад,

b) дробова частина зменшуваного менше дробової частини від’ємника; в цьому випадку одну з одиниць цілої частини зменшуваного потрібно замінити таким дробом, який їй дорівнює. Наприклад,

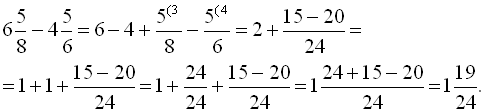
Множення звичайних дробів виконується таким чином: , тобто перемножують окремо чисельники, окремо знаменники. Перший добуток роблять чисельником, другий – знаменником. Отриманий дріб, якщо це можливо, скорочують.

При множенні мішаних дробів їх попередньо зображають у вигляді неправильних дробів, а потім перемножують. Наприклад,

.

При діленні дробу на дріб чисельник діленого множать на знаменник дільника, а знаменник діленого – на чисельник дільника. Перший добуток служить чисельником, а другий – знаменником частки: . Наприклад,.

Якщо потрібно поділити дріб на дріб, у випадку коли один чи обидва дроби – мішані, то потрібно попередньо зобразити мішаний дріб у вигляді неправильного дробу.

Будь-яку ціле число можна зобразити у вигляді дробу. Наприклад,

,

Приклад.5

Обчислити

.

Розв’язання

     1) ;

     2) ;

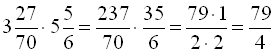     3) ;

     4) ;

     5) .

Відповідь: 2,5.

Завдання №6

Доволі багато задач в математиці присвячено темі модуля. Дамо визначення поняття модуля.

Найчастіше він зустрічається при розв’язанні ірраціональних рівнянь та нерівностей

Задача зводиться до задачі з модулем

Відповідно до визначення поняття модуля, можна зробити висновок, що для того щоб відкрити модуль потрібно визначити знак під модульного виразу і застосувати власне визначення. Розглянемо безпосередньо на прикладі

Приклад.6

Знайти значення виразу, розкривши знак модуля з відповідним знаком

Розв’язання

√	31	=	5,567764363
√	23	=	4,795831523
√	31	+	√	23	=	10,3635959
√	31	+	√	23	-	10	=	0,3636	>0
√	31	+	√	23	-	17	=	-6,636	<0

Відповідь:7.