матриць (2.7) – (2.11) відповідно до (2.6), підставити конкретні значення x0, y0, z0, nx, ny, nz, d, та отримати результат.

Рекомендована література [1, 4, 6, 7, 13, 15] Питання для перевірки знань:

1.Наведіть способи отримання даних?

2.Дайте характеристику векторних моделей даних?

3.Що таке поняття векторної топології?

4.Для чого використовуються растрові моделі даних?

5.Переваги і недоліки растрових і векторних моделей?

3. Поняття про просторові та атрибутивні дані

Кожен географічний об’єкт має один або більше атрибутів, які ідентифікують даний об’єкт. Вибір типу аналізу частково залежить і від типу використовуваних атрибутів.

Типи атрибутивних величин. До атрибутивних величин відносять: категорії, ранги, кількість, величину, відношення.

Категорії. Категоріями є групи подібних об’єктів. Вони допомагають краще відобразити суть даних. Об’єкти одного класу завжди якимось чином подібні між собою і мають характерні відмінності від іншого класу. Наприклад в категорію доріг можна віднести автостради, шосе або інші дороги. Значення категорій можуть бути представлені у вигляді числового коду або тексту. Текстові значення часто приводяться в скороченому вигляді з метою економії місця в таблиці.

Ранги. Ранги систематизують об’єкти в порядку зростання або зниження величин. Як правило, вони використовуються, коли безпосередня оцінка величини затрудняється або визначається поєднанням факторів. Такий вид оцінки відносний.

Кількість і величина. Відбивають числові значення. Кількість відбиває фактичне число об’єктів заданого виду на карті. Використання показника кількість або величина дозволяє бачити реальне значення кожного об’єкту і співставляти його з наченнями сусідніх.

Відношення. Показує взаємозв’язок між двома величинами і визначається для кожного об’єкту шляхом поділу однієї величини на іншу. Використання відносних показників відбиває різницю між великими і малими площами, які мають меншу їх кількість. Таким чином, карта більш об’єктивно може показувати розподіл об’єктів.

Постановка задачі. Видалення (блокування виведення на екран) невидимих ділянок ліній та поверхонь (задача загороджування) є одним із найважливіших та найважчих етапів створення на комп ютері якісного та реалістичного зображення 3D-об єктів та 3D-сцен за короткий час.

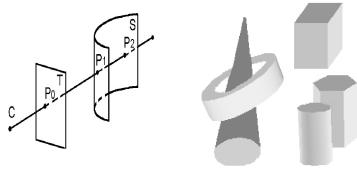
З проективної геометрії відомо, що деяка точка Р1 поверхні S загороджує точку Р2 цієї поверхні, якщо: проекції цих точок на картинну площину Т при заданому центрі проектування та спостереження С співпадають; СР1 СР2 (рис.3.1). Деяку точку поверхні називають видимою, якщо вона не загороджена жодною іншою точкою цієї поверхні або інших об’єктів 3D-сцени.

Задача видалення невидимих ділянок ліній та поверхонь природно зводиться до виявлення видимих частин цих ліній та поверхонь та зображення їх на картинній площині. Незважаючи на існування численних загальних концепцій розв язування задач загороджування, відсутній універсальний алгоритм їх розв язуван-ня. Натомість є ефективні методи розв язування окремих класів задач загороджування.

Загальні концепції розв язування задач загороджування. Нехай геометрична 3D-сцена складається з певної кількості фрагментів (об єктів) А1,А2,..,АN (рис.3.2). Тоді для будь-якої пари фрагментів Аі та Аj потрібно встановлювати такі факти: якщо жоден із фрагментів Аі та Аj не загороджує інший, то їх можна обробляти незалежно один від одного; якщо фрагмент Аі повністю або частково загороджує фрагмент Аj, а фрагмент Аj не загороджує фрагменту Аі, то встановлюють певний пріоритет їх обробки (спочатку – фрагмент Аj, а потім – фрагмент Аі); якщо фрагменти Аі та Аj частково загороджують один одного, то доцільно розбити ці фрагменти на складові частини та повернутися до першого або другого варіантів.

Уцілому, задача встановлювання факту загороджування одним об єктом іншого об єкту може бути розв язана двома способами: у просторі об єктів (шляхом аналізу взаємного розташування геометричних фігур); у просторі проекцій (шляхом аналізу взаємного розташування проекцій геометричних фігур на картинну площину).

Уразі аналізу взаємного розташування 3D-фігур, пріоритет їх обробки встановлюють так: знаходять найдальші та найближчі точки фрагментів по відношенню до спостерігача (або до картинної площини) та аналізують їх розташування (якщо найдальша точка фрагменту Аі лежить ближче до спостерігача, ніж найближча точка фрагменту Аj, то Аj не загороджує Аі); в об єктному просторі знаходять площину, що розділяє його на два напівпростори, в одному з яких знаходяться фрагмент Аi та спостерігач, а в іншому – фрагмент Аj (тоді Аj не може загороджувати Аi).

Уразі аналізу проекцій, незалежна обробка геометричних фігур можлива тоді, коли проекції цих фігур не перетинаються.

Для ефективного розв язування задач загороджування, правила обчислення пріоритету та встановлення факту незалежності фрагментів 3D-сцени повинні бути простими. Тому початкову задачу загороджування необхідно подрібнювати та

спрощувати до такого стану, щоб її можна було розв’язати на основі простих правил.

Якщо початкові геометричні фігури мають складну форму, доцільно розбити їх на простіші складові частини або помістити, як в оболонку, всередину простіших геометричних фігур (кулі, куба, паралелепіпеда), та працювати з цими оболонками (вони повинні бути мінімальними). Якщо проекції мають складні форми, їх теж розбивають на простіші складові частини або поміщають до мінімальних простих оболонок (до прямокутників зі сторонами, паралельними осям координат).

Класифікація методів розв’язування задач загороджуван-ня. Базовими для цієї класифікації є такі поняття: дозвіл картинної площини (кількість точок растру або пікселів на екрані монітору); дозвіл многогранної поверхні (кількість її граней); глибина елементу поверхні або лінії (відстань від нього до картинної площини). Найвідоміші методи розв’язування задач загороджування можна класифікувати за чотирма наведеними нижче характеристиками.

По-перше, за вибраним типом формалізованого опису дос-ліджуваної поверхні або лінії (за тим математичним апаратом та структурами даних, які було вибрано для її подання), виділяють три класи методів, які використовують такі подання: аналітичне (за допомогою аналітичного виразу); поліедральне, тобто многогранне (за допомогою сукупності многокутних граней); параметричне .

По-друге, за вибраним типом простору, в якому здійснюють аналіз видимості частин досліджуваних поверхонь або ліній, виділяють такі класи методів: об’єктні (аналіз видимості здійснюють в об’єктному просторі, час роботи методів є квадратичною функцією від кількості об’єктів 3D-сцени та їх дозволу); картинні (аналіз видимості здійснюється в площині зображення, час роботи методів є лінійною функцією від добутку кількості об’єктів на кількість точок растру); змішані.

По-третє, за обраним способом візуалізації поверхні виділяють такі класи методів: ті, що орієнтовані на отримання каркасного зображення (лінії

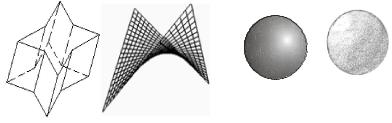
сітки параметричного подання та ребра много-гранника називають каркасними лініями, а саме зображення – каркасним – рис.3.3); ті, що орієнтовані на отримання напівтонового зображення (з використанням напівтонового зафарбовування елементів поверхні або накладання на неї текстури, з урахуванням впливу на цю текстуру джерел світла – рис. 3.4).

По-четверте, методи розв’язування задач загороджування розрізняють за специфічними геометричними властивостями 3D-об’єктів, 3D-сцен та їх проекцій, використаними в процесі роботи.

Застосування до розв язування задачі загороджування тих чи інших методів суттєво залежить від форми, властивостей та взаємного розташування компонентів 3D-сцен. Слід окремо виділити опуклі многогранники та гладкі несамоперетинні поверхні: завдяки їх гарній структурованості та впорядкованості, видимість кожного елементу 3D-сцени залежить від видимості найближчих елементів та змінюється регулярно (кожна грань опуклого многогранника або повністю видима, або повністю невидима). У разі неопуклих многогранних поверхонь, видимість теж змінюється регулярно. Але цих властивостей не буде мати 3D-сцена з довільних, невпорядковано розкиданих у просторі многокутників.

Важливою характеристикою методу розв язування задачі загороджування є асимптотичний час роботи алгоритму залежно від дозволу зображуваного об’єкту та картинної площини (він може бути пов язаний з властивостями об’єкту, внутрішньою структурою використаного алгоритму та іншими факторами).

Найбільш розповсюдженими на практиці методами розв’язу-вання задач

допомогою активних вікон, кеширування вздовж регулярної прямокутної сітки, художника, поточних обріїв, двійкового розбиття об єктного простору, порядкового сканування.

Оглядовий аналіз базових методів розв’язування задач загороджування. Розглянемо сутність, характеристику практичного застосування та продуктивності основних класів методів розв я-зування задач загороджування.

1. Метод прямого перебирання.

Сутність методу. Аналіз видимості об’єктів 3D-сцени передбачає пряме перебирання цих об’єктів. Розглядають кожне ребро кожного об’єкту сцени та аналізують його взаємне розташування з усіма гранями.

Якщо ребро перетинає ту напівплощину, що містить грань, то розглядають окремо частини ребра, розділені точкою перетину.

Якщо ж ребро не перетинає грань, то перевіряють, чи знаходиться це ребро в тому ж напівпросторі відносно грані, що й спостерігач.

Характеристика методу. Застосовується для побудови каркасних зображень. Час роботи цього методу квадратично залежить від кількості елементів сцени (дозволу об єктів), оскільки є пропор-ційним добутку кількості ребер та граней сцени.

2. Метод буферу глибини (Z-буферу).

Сутність методу. Використовуються дві області пам’яті:

–Z-буфер (він же – буфер глибини) зберігає координату Z (глибину) кожного пікселя картинної площини, що є видимим на поточному кроці аналізу зображення;

–буфер кадру містить інформацію про стан атрибутів пікселів (інтенсивності та кольору).

Технологія роботи за методом Z-буферу така.

Крок 1: ініціалізують буфер глибини значенням глибини фону, а буфер кадру – значеннями атрибутів фону. Крок 2: будують растрову розгортку проекції поточної грані. Крок 3: для кожного пікселя (xi,yj) цієї розгортки

обчислюють глибину zij . Крок 4: по-рівнюють значення zij з відповідним пікселю (xi,yj) значенням zij(Buf), що зберігається в буфері глибини; якщо zij < zij(Buf) (zij знаходиться ближче), то zij(Buf) присвоюють значення zij, заносячи його до відповідної позиції буферу глибини, а атрибути пікселя zij записують до буферу кадру. Крок 5: переходять до наступної необробленої грані та до

кроку 2.

Характеристика методу. Використовується для зображення складних сцен із застосуванням ортогонального проектування на картинну площину. Нескладна модифікація методу дозволяє отримувати перерізи поверхонь паралельними площинами.

Час роботи цього методу: лінійно залежить від кількості точок растру та глибинної складності сцени (усередненої кількості граней, які взаємно закривають одна одну); не залежить від дозволу об’єкту.

Метод Z-буферу є зручним для апаратної реалізації завдяки простоті алгоритму та використаного в цьому алгоритмі набору операцій.

3.Метод видалення нелицьових граней.

Сутність методу. Деяку грань многогранника називають лицьовою (нелицьовою), якщо: зовнішня нормаль до грані та центр проектування знаходяться в одному (різних) напівпросторах відносно площини, що містить грань – у разі центрального проектування; вектор зовнішньої нормалі до

грані та вектор проектування утворюють гострий (тупий) кут – у разі паралельного проектування. При проектуванні многогранника на картинну площину, нелицьові грані будуть невидимими. Це вдвічі скорочує кількість граней, які потрібно аналізувати на видимість. Для опуклих багатогранників цей метод дає повний розв язок задачі – достатньо видалити всі нелицьові грані. Для неопуклих багатогранників додатково аналізують на видимість лицьові грані.

Характеристика методу. Використовується для побудови зображень многогранників на картинній площині з використанням центральної проекції з заданим центром проектування або ортогональної проекції з заданим напрямним вектором. Час роботи методу є пропорційним кількості граней.

4. Методи аналізу кількісної невидимості точок поверхні.

Сутність методів. У основу цих методів покладено такі поняття: точка гладкої поверхні є регулярною точкою відображення проектування поверхні на картинну площину, якщо вона разом зі своєю малою околицею може бути взаємно однозначно спроектована на цю площину; контурними лініями гладкої поверхні називають зв’язні компоненти, що входять до складу множини нерегулярних точок деякого відображення проектування цієї поверхні на картинну площину (як правило, це гладкі криві).

Ці методи базуються на впровадженні функції кількісної невидимості точок гладкої поверхні (значенням функції у фіксованій точці поверхні є кількість тих точок, які закривають її). Властивості вказаної функції дозволяють звести задачу загороджування на гладкій поверхні до вивчення поведінки цієї функції на контурних лініях, видимі частини яких є обрисами поверхні. Аналізуючи величини стрибків функції, виявляють: ділянки поверхні, що загороджені складками інших ділянок цієї поверхні; ділянки загороджування поверхнею самої себе в околицях точок зборки проектування.

Характеристика методів. Використовуються для розв’язування задач загороджування на гладких поверхнях та (при складнішому процесі аналізу) на многогранних поверхнях. Підсумком роботи методів є контурне зображення, що заповнюють каркасними лініями або напівтоновим зафарбовуванням (для цього використовують властивості функції кількісної невидимості в таких точках, які є прообразом регулярних значень відображення проектування). Час роботи методів лінійно залежить від дозволу поверхні, що є найкращим результатом для алгоритмів, які працюють в об’єктному просторі.

5. Метод розбиття картинної площини за допомогою активних вікон. Сутність методу. Використовується поняття активного вікна –

геометричної області, яку можна пересувати вздовж картинної площини та розбивати на вікна меншого розміру.

Вміст поточного активного вікна аналізують на взаємне розташування з проекціями елементів 3D-сцени (найчастіше – з многокутниками, що є проекціями граней многогранників).

Упідсумку аналізу, який можна проводити за різними системами правил) розглядають такі типові випадки: якщо вікно повністю покрите проекцією найближчого за глибиною елементу сцени, то зафарбовування вікна здійснюють кольором цієї проекції; якщо до вікна не потрапила жодна з проекцій елементів сцени, то його зафарбовують кольором фону; в разі невиконання двох перших умов, вікно розбивають на чотири частини та повторюють аналіз для кожної з них.

Подрібнення вікна можна здійснювати до розміру пікселя картинної площини.

Упідсумку роботи методу, отримують подання зображення в вигляді тетрарного дерева, листки якого зберігають атрибути кольору та інтенсивності відповідних активних вікон.

Характеристика методу. Застосовується для аналізу видимості сцен, складених із многогранних поверхонь. Для підвищення ефективності методу, вдосконалюють: правила формування, аналізу та розбиття активного вікна (для скорочення кількості операцій розбиття); метод аналізу взаємного розташування вікна та проекцій елементів 3D-сцени (для скорочення кількості перевірочних дій). Час роботи методу залежить від щільності розташування проекцій елементів 3D-сцени та може бути скорочений завдяки застосуванню для аналізу зображення паралельних обчислень.

6. Метод кеширування вздовж регулярної прямокутної сітки. Сутність методу. Метод базується на такій властивості: як-що

проекції ребра та грані многогранника можна розмістити в прямокутних оболонках зі сторонами, паралельними координатним осям, та ці оболонки не перетинаються, то: проекції не перетинаються; ребро повністю видиме відносно грані. Цю пару "ребро-грань" можна вилучити з подальшого аналізу ребра многогранника на виявлення видимих ділянок.

Для реалізації методу, на картинну площину накладають регулярну сітку з прямокутними чарунками. Для кожної чарунки складають список граней, проекції яких її перетинають. Для кожного ребра: складають список чарунок, які перетинає його проекція; аналізують на видимість лише ті пари "ребро-грань", проекції яких мають загальні чарунки перетину.

Характеристика методу. Дозволяє уникнути прямого перебирання комбінацій "ребро-грань" многогранника в процесі аналізу взаємного розташування проекцій ребер та граней, націленого на виявлення видимих ділянок ребер (кількість операцій аналізу та час їх виконання стають на порядок меншими, але потрібна додаткова пам’ять для зберігання списків чарунок перетину).

7. Метод художника.

Сутність методу. Базова технологія зображення в ортогональній проекції довільної поверхні, визначеної як функція від двох змінних на прямокутній сітці, є наступною: виконують тріангуляцію області визначення функції та кусково-лінійну апроксимацію початкової (дискретно заданої) поверхні многогранною поверхнею з трикутними гранями; призначають вузлам сітки таку нумерацію (xi,yj) (i = 0,…,M-1, j = 0,…,N-1), щоб було встановлено відповідність між зростанням номерів i, j та збільшенням відстані від спостерігача; проекції граней (їх зафарбовують кольорами відповідних граней) скидають на картинну площину в зворотному порядку (проекції граней, що лежать далі від спостерігача, обробляють раніше).

Характеристика методу. Належить до методів пріоритетів, ознакою яких є обов’язкове попереднє впорядковування елементів сцени за деяким параметром, наприклад, за глибиною елементу в сцені. Дає якісне напівтонове зображення поверхні. Завдяки попередньому впорядковуванню, знижується кількість операцій аналізу взаємного розташування, тобто економиться час.

8. Метод поточних обріїв.

Сутність методу. На відміну від методу художника, скидає на картинну площину проекції ребер у прямому порядку. При такому підході, формуються межі області, забороненої для подальшого втручання (побудованої частини зображення): всередині цієї області розміщують ту частину 3D-сцени, що розташована ближче до спостерігача, ніж необроблені елементи сцени. Тому проекції необроблених елементів не повинні загороджувати тієї частини сцени, зображення якої вже отримане на екрані. Максимальну та мінімальну межі області побудованого зображення називають верхнім та нижнім поточними обріями (в процесі роботи методу, їх положення змінюється).

Для враховування факту наявності забороненої зони, використовують такі типові прийоми: для зображення проекції ребра, застосовують алгоритми растрової разгортки (попіксельного рисування) відрізку; виводять тільки ті точки проекції ребра, що знаходяться зовні забороненої області, визначеної верхнім та нижнім поточними обріями.

Характеристика методу. Належить до методів пріоритетів (з відповідною економією часу роботи). Використовується для побудови каркасних зображень поверхонь, які кусково-лінійно апроксимовані на базі стандартної тріангуляції регулярної прямокутної сітки.

9. Метод двійкового розбиття об єктного простору.

Сутність методу. Базується на концепціях методу художника, тобто: грані попередньо впорядковують за зростанням їх відстані від спостерігача; проекції скидають на картинну площину в зворотному порядку.

Для впорядковування граней, використовують особливий підхід, який базується на наведених нижче домовленостях.

На першому кроці методу фіксують одну довільну грань 3D-сцени. Якщо деяка інша грань перетинає площину, що містить фіксовану грань, то її розбивають лінією перетину на дві окремі грані.

Далі грані 3D-сцени розбивають відносно фіксованої грані на дві підгрупи:

–ті грані, що лежать в одному напівпросторі зі спостерігачем відносно фіксованої грані (тобто не можуть бути загороджені фіксованою гранню);

–ті грані, що лежать у різних напівпросторах зі спостерігачем відносно фіксованої грані (тобто фіксована грань не може бути загороджена жодною з граней цієї групи).

На кожному наступному кроці методу, для кожної з виділених на попередньому кроці підгруп граней, процес фіксації певної грані та розбиття на дві підгрупи повторюють.

У підсумку, отримують впорядковане бінарне дерево, кожен вузол якого містить інформацію про деяку фіксовану грань, ліва (від вузла) гілка – про лицьові (по відношенню до фіксованої) грані, права (від вузла) гілка – про нелицьові грані.

Для отримання зображення, активізують алгоритм рекурсив-ного обходу бінарного дерева в напрямку "праве піддерево – коренева грань – ліве піддерево", з паралельним скиданням на площину проекцій тих граней, що відповідають поточним вершинам.

Характеристика методу. Належить до методів встановлення пріоритетів. Може успішно використовуватися для створення каркасних та напівтонових зображень. Аналіз геометричної 3D-сцени виконується виключно в об’єктному просторі. Робота методу не базується на враховуванні форми або перетинів граней.

10.Метод порядкового сканування.

Сутність методу. Базовим кроком методу є аналіз взаємного розташування відносно спостерігача та розв’язування задачі загороджування для множини прямолінійних відрізків, що утворюються в процесі перетину граней 3D-сцени горизонтальною площиною, котрій поставлено у відповідність горизонтальний рядок растрової розгортки екрану.

При формуванні зображення, розглядають ряд горизонтальних площин, що в цілому відповідає всім рядкам растрової розгорт-ки зображення на екрані.

Характеристика методу. Може формувати напівтонові та каркасні зображення. Працює в об’єктному просторі та в площині зображення. Дозволяє враховувати геометричні властивості 3D-сцени. В растровій модифікації часто використовується для апаратної реалізації.

Список рекомендованої літератури [2, 3, 7, 14, 15]