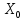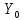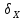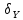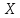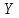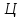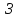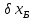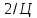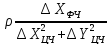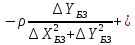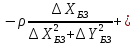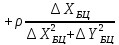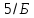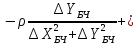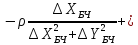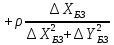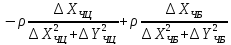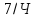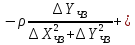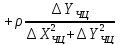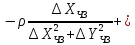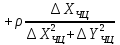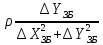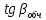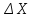- •Харківський національний університет міського господарства імені о. М. Бекетова
- •1 Лабораторні роботи
- •1.1 Математичне опрацювання рівноточних вимірювань однієї величини
- •Порядок роботи
- •1.2 Математичне опрацювання нерівноточних вимірювань однієї величини
- •Порядок роботи
- •1.3 Математичне опрацювання подвійних рівноточних вимірювань
- •Порядок роботи
- •1.4 Математичне опрацювання подвійних нерівноточних вимірювань
- •Порядок роботи
- •1.5 Оцінка точності функцій виміряних величин
- •Порядок роботи
- •2. Розрахунково-графічна робота
- •1.1 Зрівнювання геодезичного чотирикутника параметричним методом
2. Розрахунково-графічна робота
1.1 Зрівнювання геодезичного чотирикутника параметричним методом
Зміст роботи. На місцевості побудована мережа у вигляді геодезичного чотирикутника. Відомі координати двох вихідних пунктів і значення виміряних напрямків всередині чотирикутника. Необхідно знайти координати двох шуканих пунктів, які максимально відповідали б їх дійсним значенням.
Робота складається з двох етапів: зрівнювання результатів вимірювань параметричним методом; оцінка точності вимірювань.
Вихідні дані. Видаються викладачем за індивідуальним номером варіанту.
Задача.
За відомими координатами вихідних
пунктів
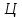 і
і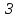 (табл. 6) і виміряними напрямками (табл.
5) виконати зрівнювання геодезичного
чотирикутника
(табл. 6) і виміряними напрямками (табл.
5) виконати зрівнювання геодезичного
чотирикутника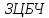 ,
знайти координати шуканих пунктів
,
знайти координати шуканих пунктів і
і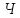 ,
та виконати оцінку точності вимірювань.
,
та виконати оцінку точності вимірювань.
Таблиця 5 – Виміряні напрямки
|
Станція |
Пункт візування |
Виміряний напрямок |
|
З |
Ц |
0° 00' 00.00'' |
|
Б |
39° 54' 56.15'' | |
|
Ч |
83°45' 10.40'' | |
|
Ц |
З |
0° 00' 00.00'' |
|
Б |
262° 07' 42.15'' | |
|
Ч |
314° 24' 44.61'' | |
|
Б |
З |
0° 00' 00.00'' |
|
Ц |
42° 12' 46.55'' | |
|
Ч |
321° 38' 06.33' | |
|
Ч |
З |
0° 00' 00.00'' |
|
Ц |
50° 39' 35.69'' | |
|
Б |
97° 47' 50.32'' |
Спочатку
будуємо схему геодезичної мережі в
масштабі 1:50000 (рис. 2). Для цього на
окремому аркуші паперу креслимо дві
взаємно перпендикулярні осі –
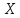 та
та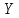 ,
і оцифровуємо їх відповідно до заданого
масштабу. Початок координат обираємо
довільно, але так, щоб схема мала компактні
розміри.
,
і оцифровуємо їх відповідно до заданого
масштабу. Початок координат обираємо
довільно, але так, щоб схема мала компактні
розміри.
Наносимо
на схему вихідні пункти
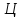 і
і за їх прямокутними координатами та
з’єднуємо їх прямою лінією. З вихідних
пунктів за допомогою транспортиру
будуємо виміряні напрямки (табл. 5) на
шукані пункти
за їх прямокутними координатами та
з’єднуємо їх прямою лінією. З вихідних
пунктів за допомогою транспортиру
будуємо виміряні напрямки (табл. 5) на
шукані пункти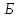 і
і .
.

Рис. 2 –Схема геодезичного чотирикутника
Таблиця 6 – Координати вихідних і шуканих пунктів
|
Назва пункту |
Наближені координати, м |
Поправки, м |
Вихідні і зрівняні координати, м | |||
|
|
|
|
|
|
| |
|
|
- |
- |
- |
- |
3123495.600 |
7017455.084 |
|
|
- |
- |
- |
- |
3120644.561 |
7017479.980 |
|
|
3123892,047 |
7020148,946 |
-0,006 |
-0,011 |
3123892,041 |
7020148,935 |
|
|
3120953,964 |
7020095,120 |
0,005 |
-0,031 |
3120953,969 |
7020095,090 |
За
виміряними напрямками обчислюємо
значення горизонтальних кутів, результати
заносимо до табл. 7 (колонка 4). Наприклад,
перший кут, виміряний зі станції
 ,
буде дорівнювати різниці напрямків на
пункти
,
буде дорівнювати різниці напрямків на
пункти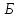 і
і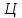
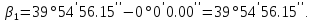
Підраховуємо
кількість невідомих
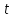 ,
якими в даному випадку є координати
,
якими в даному випадку є координати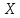 і
і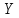 шуканих пунктів
шуканих пунктів і
і ,
тобто
,
тобто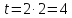 .
Число незалежних вимірювань
.
Число незалежних вимірювань
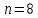 .
Число надлишкових вимірювань, відповідно,
становить
.
Число надлишкових вимірювань, відповідно,
становить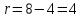 .
.
Таблиця 7 – Виміряні і зрівняні кути
|
№ кута |
Вільні члени, сек |
Кути, обчислені за наближеними координатами |
Виміряні кути |
Поправ-ки, сек |
Зрівняні кути |
|
1 |
0 |
39° 54' 56.15'' |
39° 54' 56.15'' |
-0.24 |
39° 54' 55.91'' |
|
2 |
0 |
45° 35' 15.39'' |
45° 35' 15.39'' |
-0.98 |
45° 35' 14.41'' |
|
3 |
0 |
52° 17' 02.46'' |
52° 17' 02.46'' |
0.66 |
52° 17' 03.12'' |
|
4 |
-0.55 |
42° 12' 46.00'' |
42° 12' 46.55'' |
0.02 |
42° 12' 46.57'' |
|
5 |
2.99 |
38° 21' 56.66'' |
38° 21' 53.67'' |
1.38 |
38° 21' 55.05'' |
|
6 |
0.25 |
47° 08' 14.88'' |
47° 08' 14.63'' |
0.64 |
47° 08' 15.27'' |
|
7 |
-1.48 |
50° 39' 34.21'' |
50° 39' 35.69'' |
0.19 |
50° 39' 35.88'' |
|
8 |
0 |
43° 50' 14.25'' |
43° 50' 14.25'' |
-0.44 |
43° 50' 59.25'' |
|
∑ |
|
360° 00' 00.00'' |
359° 59' 58.79'' |
1.21 |
360° 00' 00.00'' |
За
виміряними кутами (табл. 7) та координатами
вихідних пунктів (табл. 6) обчислюємо
наближені координати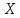 і
і
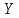 шуканих пунктів
шуканих пунктів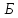 і
і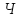 .
Використовуємо для цього допоміжну
схему взаємного розміщення пунктів в
трикутнику (рис. 3) і формули Юнга
.
Використовуємо для цього допоміжну
схему взаємного розміщення пунктів в
трикутнику (рис. 3) і формули Юнга
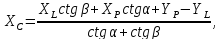
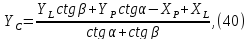
де
 –
координати
лівого
пункту
–
координати
лівого
пункту
 і
правого пункту
і
правого пункту
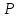 відповідно.
відповідно.
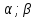 – кути
трикутника, вершинами яких є відповідно
пункти
– кути
трикутника, вершинами яких є відповідно
пункти
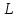 і
і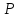 .
.
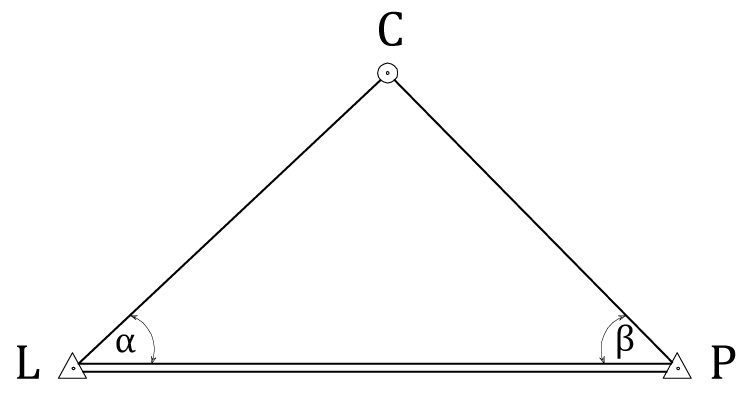
Рис. 3 – Пояснювальна схема до формул (40)
При
позначенні вершин трикутника керуються
таким правилом: якщо дивитися із середини
базисної сторони трикутника на шуканий
пункт, то ліворуч буде знаходитися
вихідний пункт
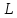 і виміряний кут
і виміряний кут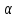 ,
а праворуч – вихідний пункт
,
а праворуч – вихідний пункт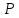 і виміряний кут
і виміряний кут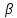 .
.
Застосувавши
це правило, виділяємо з чотирикутника
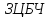 два
трикутники
–
два
трикутники
–
 і
і
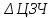 .
.
Підставляємо
в формули (40) числові значення та отримуємо
наближені координати пунктів
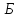 і
і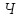 .
Обчислення виконуємо в табл. 8. Результати
заокруглюємо до 0.001 м.
.
Обчислення виконуємо в табл. 8. Результати
заокруглюємо до 0.001 м.
Таблиця 8 – Обчислення наближених координат шуканих пунктів
|
Назва пункту |
Виміряні кути |
Координати | |
|
|
| ||
|
Ц |
97° 52' 17.85'' |
3123495,600 |
7017455,084 |
|
З |
39° 54' 56.15'' |
3120644,561 |
7017479,980 |
|
Б |
|
3123892,047 |
7020148,946 |
|
Ц |
45° 35' 15.39'' |
3123495,600 |
7017455,084 |
|
З |
83° 45' 10.40'' |
3120644,561 |
7017479,980 |
|
Ч |
|
3120953,964 |
7020095,120 |
Обчислені
наближені координати пунктів
 і
і
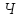 заносимо до табл. 6. Складаємо рівняння
поправок до виміряних кутів
заносимо до табл. 6. Складаємо рівняння
поправок до виміряних кутів
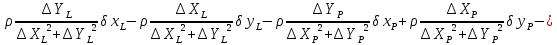
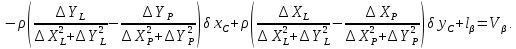
де
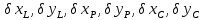 – поправкидо
наближених
координат;
– поправкидо
наближених
координат;
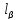 –вільний
член рівняння поправок;
–вільний
член рівняння поправок;
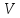 –поправка
до виміряного кута.
–поправка
до виміряного кута.
Вільні члени рівнянь поправок обчислюємо за формулою
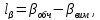 (41)
(41)
де
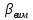 –виміряний
кут;
–виміряний
кут;
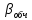 –кут,
обчислений
за наближеними координатами.
–кут,
обчислений
за наближеними координатами.
Кути, обчислені за наближеними координатами, отримуємо із виразу
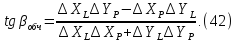
Для спрощення обчислень заповнюємо табл. 9, в якій представляємо коефіцієнти рівнянь поправок в буквеному позначенні.
Таблиця 9 – Коефіцієнти рівнянь поправок в буквеному позначенні
|
Пункт
Кут |
Поправки до наближених координат | |||
|
|
|
|
| |
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
------------------- |
------------------- |
|
|
------------------- |
------------------- |
|
|
|
|
|
|
|
|
|
|
|
|
------------------- |
------------------- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
------------------- |
------------------- |
|
|
|
|
|
|
|
|
Підставивши
в формулу
(42),
вихідні
координати пунктів
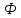 і
і
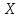 та наближені координати пунктів
та наближені координати пунктів
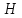 і
і
 ,
обчислюємо
тангенси кутів
,
обчислюємо
тангенси кутів
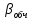 .Значення
кутів отримуємо через арктангенс.
Обчислення представлені
в табл. 10.
Контроль
обчислень – сума кутів повинна дорівнювати
360°.
.Значення
кутів отримуємо через арктангенс.
Обчислення представлені
в табл. 10.
Контроль
обчислень – сума кутів повинна дорівнювати
360°.
Кути, обчислені за наближеними координатами, заносимо до табл. 10 (колонка 3). За формулою (41) обчислюємо вільні члени рівнянь поправок, результати заносимо до табл. 7 (колонка 2).
Таблиця 10 – Обчислення кутів за наближеними координатами
|
№ кута |
Напрямок |
Приріст |
Тангенс кута
|
Значення кута
| ||
|
|
| |||||
|
1 |
ЗЦ |
2851,039 |
-24,896 |
0,83659243 |
39° 54' 56.15'' | |
|
ЗБ |
3247,486 |
2668,966 | ||||
|
2 |
ЦЧ |
309,403 |
2615,140 |
-9,13519097 |
45° 35' 15.39'' | |
|
ЦЗ |
-2851,039 |
24,896 | ||||
|
3 |
ЦБ |
396,447 |
2693,862 |
1,29310312 |
52° 17' 02.46'' | |
|
ЦЧ |
-2541,636 |
2640,036 | ||||
|
4 |
БЗ |
-3247,486 |
-2668,966 |
0,90715109 |
42° 12' 46.00'' | |
|
БЦ |
-396,447 |
-2693,862 | ||||
|
5 |
БЧ |
-2938,083 |
-53,826 |
0,79161705 |
38° 21' 56.66'' | |
|
БЗ |
-3247,486 |
-2668,966 | ||||
|
6 |
ЧЦ |
2541,636 |
-2640,036 |
1,07754038 |
47° 08' 14.88'' | |
|
ЧБ |
2938,083 |
53,826 | ||||
|
7 |
ЧЗ |
-309,403 |
-2615,140 |
1,22000091 |
50° 39' 34.21'' | |
|
ЧЦ |
2541,636 |
-2640,036 | ||||
|
8 |
ЗБ |
3247,486 |
2668,966 |
0,96021571 |
43° 50' 14.25'' | |
|
ЗЧ |
309,403 |
2615,140 | ||||
За
виразами, наведеними в табл. 9, використовуючи
значення
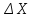 і
і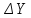 з табл. 13, обчислюємо значення коефіцієнтів
рівнянь поправок. Щоб не отримувати
занадто великих значень коефіцієнтів
рівнянь поправок і з метою запобігання
втрати точності обчислень, зменшимо
постійну
з табл. 13, обчислюємо значення коефіцієнтів
рівнянь поправок. Щоб не отримувати
занадто великих значень коефіцієнтів
рівнянь поправок і з метою запобігання
втрати точності обчислень, зменшимо
постійну
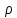 в 100 разів, тобто приймемо
в 100 разів, тобто приймемо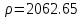 .
.
З
числових значень коефіцієнтів рівнянь
поправок формуємо матрицю  .
.
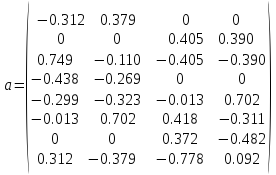 .
.
Транспонуємо
матрицю
 і помножимо її на таку ж матрицю. В
результаті отримаємо матрицю коефіцієнтів
нормальних рівнянь
і помножимо її на таку ж матрицю. В
результаті отримаємо матрицю коефіцієнтів
нормальних рівнянь .
.

Знаходимо
матрицю,
обернену
до матриці
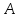 .
.
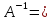
 .
.
Обчислюємо
матрицю-стовбець
вільних
членів нормальних рівнянь
 .
.
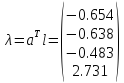 .
.
Обчислюємо
вектор-стовбець поправок до наближених
координат пунктів
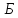 і
і
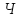 .
Результати
отримуємо
в сантиметрах.
.
Результати
отримуємо
в сантиметрах.
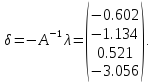
Отримані поправки заносимо до табл. 6, попередньо зменшивши їх в 100 разів, щоб розмірність була в метрах.
Знаходимо
в табл. 6
значення
зрівняних координат
шуканих
пунктів
 і
і
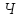 .
.
Обчислюємо вектор-стовбець поправок до виміряних кутів. Результати отримуємо в секундах.

Отримані результати заносимо до табл. 7 і обчислюємо зрівняні кути. Для контролю обчислень знаходимо суму зрівняних кутів, – вона повинна дорівнювати 360° 00' 00.00''. В даному випадку умова виконується.
На цьому зрівнювання результатів вимірювань завершено. Після зрівнювання виконуємо оцінку точності вимірювань.
Обчислюємо емпіричну середню квадратичну похибку виміряного кута за формулою
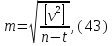
де
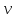 – поправка до виміряного кута;
– поправка до виміряного кута;
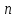 –кількість
вимірювань;
–кількість
вимірювань;
 –кількість
невідомих.
–кількість
невідомих.
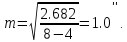
Оцінюємо надійність емпіричної середньої квадратичної похибки за формулою
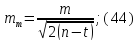
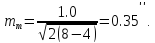
Обчислюємо середню квадратичну похибку зрівняного кута за формулою
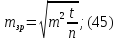
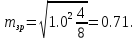
Позначивши
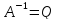 ,знаходимо
середні квадратичні похибки положення
шуканих пунктів
,знаходимо
середні квадратичні похибки положення
шуканих пунктів
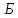 і
і
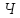 за осями координат, використовуючи
діагональні елементи матриці
за осями координат, використовуючи
діагональні елементи матриці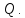
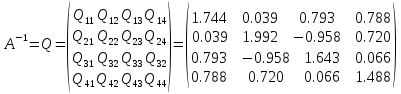 .
.
Пункт
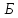 Пункт
Пункт
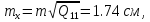

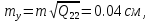
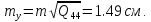
Знаходимо
кругові середні квадратичні похибки
положення пунктів
 і
і
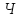 за формулою
за формулою
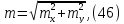
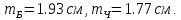
Використовуючи
елементи матриці
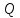 ,
знаходимо параметри еліпсів похибок
(рис. 4), орієнтування і розміри осей
якого визначають найбільш вірогідні
напрямки і величину максимальної і
мінімальної середньої квадратичної
похибки
положення пунктів
,
знаходимо параметри еліпсів похибок
(рис. 4), орієнтування і розміри осей
якого визначають найбільш вірогідні
напрямки і величину максимальної і
мінімальної середньої квадратичної
похибки
положення пунктів
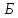 і
і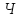 .
.
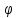
b
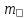
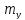

P
a
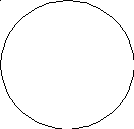
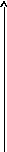




Y
V





U
Рис. 4 – Параметри еліпсу похибок
Кут повороту осей еліпсу похибок знаходимо із виразу
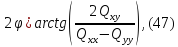
де
 – елементи матриці
– елементи матриці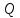 .
.
Якщо
кут
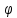 ,
обчислений за формулою (47) приймає
від’ємне значення, додаємо до нього
180°.
,
обчислений за формулою (47) приймає
від’ємне значення, додаємо до нього
180°.
Пункт
Б Пункт
Ч


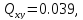
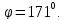
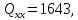
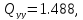
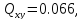
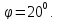
 виділяємо 2 блоки: перший відповідає
пунктуБ,
другий – пункту Ч
(в тому порядку, в якому вони були внесені
до табл. 9).
виділяємо 2 блоки: перший відповідає
пунктуБ,
другий – пункту Ч
(в тому порядку, в якому вони були внесені
до табл. 9).
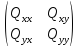
 Пункт
Б
Пункт
Б



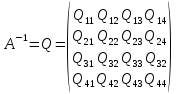
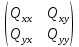
Розміри великої і малої напіввісі еліпсів похибок, відповідно, обчислюємо за формулами
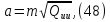

де
елементи
 і
і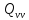 дорівнюють
дорівнюють

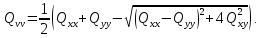
Отже,
підставивши числові значення елементів
матриці
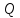 у вирази (48) і (49), отримаємо такі результати
у вирази (48) і (49), отримаємо такі результати
Пункт Б Пункт Ч
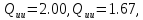
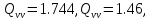
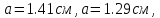
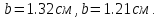
За
обчисленими параметрами еліпсів похибок
(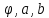 ),
будуємо
їх на схемі геодезичної мережі (рис.
5).
),
будуємо
їх на схемі геодезичної мережі (рис.
5).
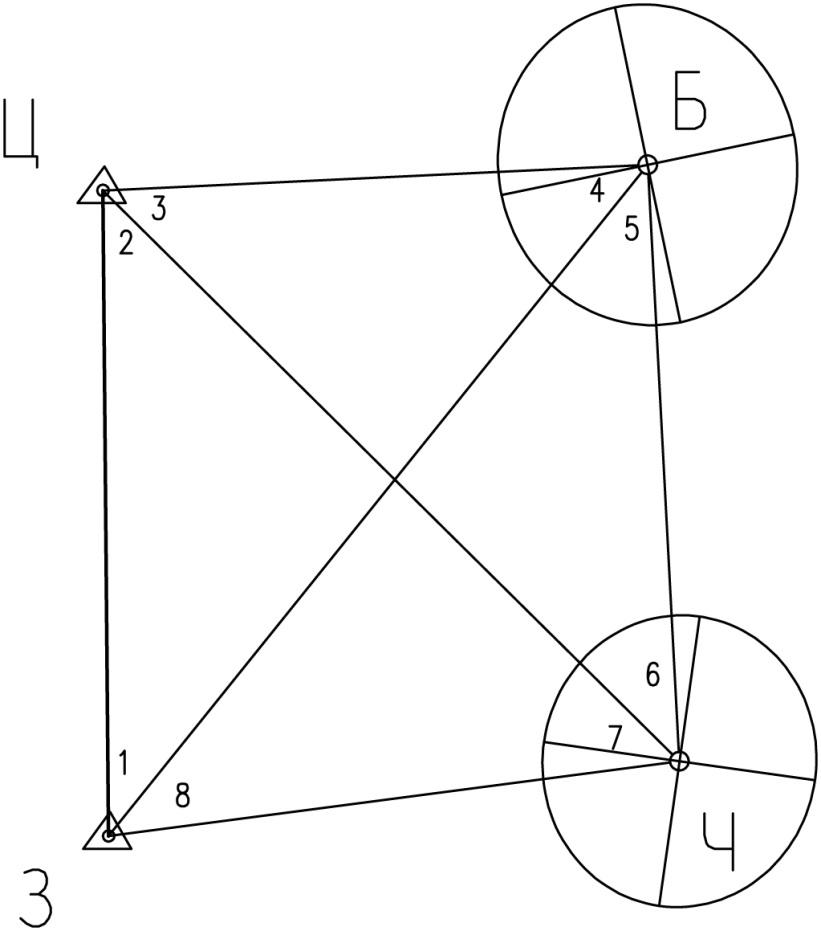
Рис. 5 – Побудова еліпсу похибок