- •Харківський національний університет міського господарства імені о. М. Бекетова
- •1 Лабораторні роботи
- •1.1 Математичне опрацювання рівноточних вимірювань однієї величини
- •Порядок роботи
- •1.2 Математичне опрацювання нерівноточних вимірювань однієї величини
- •Порядок роботи
- •1.3 Математичне опрацювання подвійних рівноточних вимірювань
- •Порядок роботи
- •1.4 Математичне опрацювання подвійних нерівноточних вимірювань
- •Порядок роботи
- •1.5 Оцінка точності функцій виміряних величин
- •Порядок роботи
- •2. Розрахунково-графічна робота
- •1.1 Зрівнювання геодезичного чотирикутника параметричним методом
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
Харківський національний університет міського господарства імені о. М. Бекетова
Кафедра ГІС, оцінки землі
та нерухомого майна
ЛАБОРАТОРНІ
ТА РОЗРАХУНКОВО-ГРАФІЧНІ РОБОТИ
з дисципліни
«Математична обробка геодезичних вимірів»
Варіант 55
Виконала: ст. гр. ГІС2012-2
Маківець Н.С.
Перевірив: Шаульський Д.В.
Харків – 2014
ЗМІСТ
Стор.
|
1. |
ЛАБОРАТОРНІ РОБОТИ………………………………………………... |
| |||
|
|
1.1 |
Математичне опрацювання рівноточних вимірювань однієї величини……………………………………………………………… |
| ||
|
|
1.2 |
Математичне опрацювання нерівноточних вимірювань однієї величини……………………………………………………………… |
| ||
|
|
1.3 |
Математичне опрацювання подвійних рівноточних вимірювань.. |
| ||
|
|
1.4 |
Математичне опрацювання подвійних нерівноточних вимірювань…………………………………………………………... |
| ||
|
|
1.5 |
Обчислення середніх квадратичних похибок функцій виміряних величин……………………………………………………………….. |
| ||
|
2 |
РОЗРАХУНКОВО-ГРАФІЧНА РОБОТА……………………………... |
| |||
|
|
2.1 |
Зрівнювання геодезичного чотирикутника параметричним методом………………………………………………………………. |
| ||
|
СПИСОК ДЖЕРЕЛ…………………………………………………………... |
| ||||
1 Лабораторні роботи
1.1 Математичне опрацювання рівноточних вимірювань однієї величини
Мета роботи: практичне застосування формул математичного опрацювання рівноточних вимірювань однієї величини; засвоєння методу визначення найбільш надійного або вірогіднішого значення вимірюваної величини та оцінки точності вимірювань.
Вихідні дані. Видаються викладачем за індивідуальним номером варіанту.
Зміст роботи. В результаті повторних рівноточних вимірювань однієї величини X, істинне значення якої є невідомим, отриманий ряд результатів
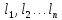 .
.
Необхідно обчислити найбільш надійне значення вимірюваної величини X, обчислити середні квадратичні похибки одного вимірювання і простої арифметичної середини результатів вимірювань. Оцінити їх надійність.
Порядок роботи
Визначити вірогідніше значення вимірюваної величини за формулою
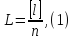
де
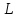 –проста
арифметична середина результатів
вимірювань;
–проста
арифметична середина результатів
вимірювань;
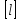 –сума
результатів вимірювань;
–сума
результатів вимірювань;
 –кількість
вимірювань.
–кількість
вимірювань.
Замість формули (1) на практиці використовують більш зручну формулу

де
 –так
званий
«умовний
нуль».
–так
званий
«умовний
нуль».
За умовний нуль зазвичай обирають найменше значення з наведеного ряду результатів вимірювань, або інше доцільно обране значення таким чином, щоб різниці
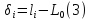
були малими величинами.
Щоб
не накопичувати похибки заокруглення,
просту арифметичну середину
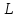 обчислюють з числом десяткових знаків
на два більше, ніж у результатах вимірів
обчислюють з числом десяткових знаків
на два більше, ніж у результатах вимірів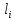 .
Потім заокруглюють це значення, залишаючи
кількість десяткових знаків на один
більше, ніж у результатах вимірювань.
Таким чином, отримують дещо зміщене
значення
.
Потім заокруглюють це значення, залишаючи
кількість десяткових знаків на один
більше, ніж у результатах вимірювань.
Таким чином, отримують дещо зміщене
значення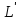 ,
яке відрізняється від
,
яке відрізняється від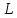 на малу величину
на малу величину
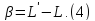
Обчислити поправки, тобто відхилення результатів вимірювань
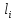 від арифметичної середини, за формулою
від арифметичної середини, за формулою
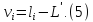
Теоретично
контролем обчислення поправок слугує
четверта властивість простої арифметичної
середини [2].
На практиці внаслідок заокруглення
простої арифметичної середини на
величину
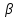 ,
за формулою (5) ми отримуємо зміщенні
поправки. Які, в свою чергу, теж
відрізняються від вірогідніших на
величину
,
за формулою (5) ми отримуємо зміщенні
поправки. Які, в свою чергу, теж
відрізняються від вірогідніших на
величину .
Тому контролем обчислення поправок
слугує рівність
.
Тому контролем обчислення поправок
слугує рівність
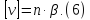
Двічі, враховуючи вираз
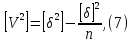
обчислити емпіричну середню квадратичну похибку окремого вимірювання за формулою
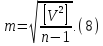
Так як емпірична середня квадратична похибка, обчислена за формулою (8) – величина наближена, то необхідно оцінити її надійність. Тобто обчислити середню квадратичну похибку середньої квадратичної похибки. Для цього застосовують формулу

Обчислити середню квадратичну похибку простої арифметичної середини за формулою
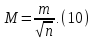
Обчислити надійність середньої квадратичної похибки простої арифметичної середини за формулою
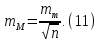
Задача. Горизонтальний кут виміряний 21 прийомом теодолітом 2Т5. Результати вимірювань наведені в табл. 1. Виконати математичне опрацювання результатів рівноточних вимірювань.
Таблиця 1 – Результати математичного опрацювання рівноточних вимірювань
|
№ |
Горизонтальний
кут,
|
сек. |
сек2. |
сек. |
сек2. |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
111˚ 44' 52.8'' |
6.6 |
43.56 |
-1.05 |
1.1025 |
|
2 |
111˚ 44' 48.1'' |
1.9 |
3.61 |
3.65 |
13.3225 |
|
3 |
111˚ 44' 48.9'' |
2.7 |
7.29 |
2.85 |
8.1225 |
|
4 |
111˚ 44' 53.1'' |
6.9 |
47.61 |
-1.35 |
1.8225 |
|
5 |
111˚ 44' 46.2'' |
0.0 |
0 |
5.55 |
30.8025 |
|
6 |
111˚ 44' 50.9'' |
4.7 |
22.09 |
0.85 |
0.7225 |
|
7 |
111˚ 44' 54.2'' |
8.0 |
64 |
-2.45 |
6.0025 |
|
8 |
111˚ 44' 46.9'' |
0.7 |
0.49 |
4.85 |
23.5225 |
|
9 |
111˚ 44' 53.6'' |
7.4 |
54.76 |
-1.85 |
3.4225 |
|
10 |
111˚ 44' 57.3'' |
11.1 |
123.21 |
-5.55 |
30.8025 |
|
11 |
111˚ 44' 52.9'' |
6.7 |
44.89 |
-1.15 |
1.3225 |
|
12 |
111˚ 44' 53.4'' |
7.2 |
51.84 |
-1.65 |
2.7225 |
|
13 |
111˚ 44' 49.8'' |
3.6 |
12.96 |
1.95 |
3.8025 |
|
14 |
111˚ 44' 53.5'' |
7.3 |
53.29 |
-1.75 |
3.0625 |
|
15 |
111˚ 44' 50.8'' |
4.6 |
21.16 |
0.95 |
0.9025 |
|
16 |
111˚ 44' 48.4'' |
2.2 |
4.84 |
3.35 |
11.2225 |
|
17 |
111˚ 44' 56.7'' |
10.5 |
110.25 |
-4.95 |
24.5025 |
|
18 |
111˚ 44' 56.5'' |
10.3 |
106.09 |
-4.75 |
22.5625 |
|
19 |
111˚ 44' 54.5'' |
8.3 |
68.89 |
-2.75 |
7.5625 |
|
20 |
111˚ 44' 51.1'' |
4.9 |
24.01 |
0.65 |
0.4225 |
|
21 |
111˚ 44' 47.1'' |
0.9 |
0.81 |
4.65 |
21.6225 |
|
Σ |
|
116.5 |
865.65 |
0.05 |
219.3525 |
За умовний нуль приймаємо найменший з результатів вимірювань горизонтального кута, тобто
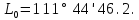
Обчисливши
за формулою (10) різниці
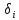 ,
находимо їх суму
,
находимо їх суму
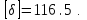
Результати обчислень заносимо до табл. 1 (колонка 3). За формулою (2) обчислюємо вірогідніше значення горизонтального кута
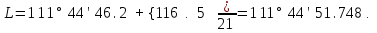
Заокруглюємо отриманий результат до 0.01''
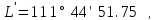
і
находимо похибку заокруглення
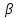 за
формулою
(4)
за
формулою
(4)
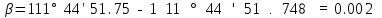
Для
оцінки
точності вимірювань обчислюємо зміщені
поправки
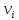 за формулою (5), і находимо їх суму.
Результати заокруглюємо до 0.01'' і заносимо
до табл. 1 (колонка 5). Виконуємо контроль
обчислень шляхом підстановки отриманих
значень в рівність (6)
за формулою (5), і находимо їх суму.
Результати заокруглюємо до 0.01'' і заносимо
до табл. 1 (колонка 5). Виконуємо контроль
обчислень шляхом підстановки отриманих
значень в рівність (6)

Находимо
квадрати поправок і їх сумарне значення
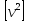 ,
результати
заокруглюємо до 0.0001 сек.2
і
заносимо до табл. 1 (колонка 6). Перевіряємо
виконання рівності (7)
,
результати
заокруглюємо до 0.0001 сек.2
і
заносимо до табл. 1 (колонка 6). Перевіряємо
виконання рівності (7)

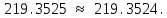
За формулою (8) обчислюємо емпіричну середню квадратичну похибку одного вимірювання
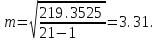
Обчислюємо середню квадратичну похибку простої арифметичної середини за формулою (10)
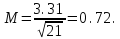
Оцінюємо
надійність величин
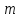 і
і
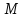 за
формулами
(9)
і
(11)
відповідно
за
формулами
(9)
і
(11)
відповідно
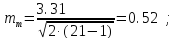
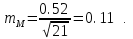
Остаточний результат математичного опрацювання рівноточних вимірювань горизонтального кута буде таким