
- •Міністерство освіти і науки, молоді та спорту україни
- •Практичне заняття № 1. Визначення області екстремуму методом крутого сходження Боксу-Уїлсона
- •Порядок роботи:
- •Залишкова сума квадратів дорівнює
- •Контрольні питання
- •Практичне заняття № 2. Узагальнений параметр оптимізації
- •Результати наведені в таблиці 2.1.
- •Для другого приватного параметра
- •Другий спосіб
- •Третій спосіб
- •Контрольні питання
- •Практичне заняття № 3. Симплекс-решітчастого планування (плани Шефе)
- •Контрольні питання
- •Практичне заняття №4 Планування експерименту з якісними факторами
- •Контрольні питання
- •Список використаних джерел
Контрольні питання
1. Для чого використовується узагальнений параметр оптимізації?
2. Що таке середнє геометричне?
3. Як визначаються коефіцієнти моделі для узагальненого параметра?
4. Яким чином розбивається шкала бажаності?
5. Яким чином проводиться обмеження шкали бажаності?
Практичне заняття № 3. Симплекс-решітчастого планування (плани Шефе)
Мета заняття – досліджити залежність октанового числа (04) суміші, що складається з трьох сортів бензину: АІ-93, А-76 і А-66, за допомогою симплекс-решітчастого планування експерименту.
Вихідні дані:
бензин АИ-93 --- Х1
бензин А-76 ----- Х2
бензин А-66 ----- Х3
октанове число (04) – У
Модель
зв’язку
![]() подається
у вигляді приведеного рівняння другого
порядку.
подається
у вигляді приведеного рівняння другого
порядку.
![]() .
.
Потрібно:
1) знайти коефіцієнти моделі;
2) перевірити однократність дисперсій виміру функції відгуку й перевірити одержану модель на адекватність.
Порядок виконання роботи
1. Визначаємо число точок плану.
Симплекс-решітчасті плани є насиченими, тобто число дослідів для цих планів дорівнює числу коефіцієнтів моделі. При цьому, число дослідів визначають за формулою числа поєднань
![]() ,
,
де
![]() – число
компонентів,
що
створюють суміш;
– число
компонентів,
що
створюють суміш;
![]() –ступінь
поліному
математичної
моделі.
–ступінь
поліному
математичної
моделі.
Оскільки
зв'язок
![]() описано
моделю
другого
порядку, то q=3, n=2.
описано
моделю
другого
порядку, то q=3, n=2.
Тому
![]() .
.
2. Складаємо матрицю симплекс-решітчасте планування другого порядку для три компонентної суміші трьох сортів бензину.
|
|
№ досліду |
Склад суміші (частка одиниці) |
Паралельні досліди |
Середнє значення октанового числа (опитне) |
Дисперсія за рядком Si | |||
|
|
Х1 |
Х2 |
Х3 |
У1 |
У2 | |||
|
|
1 |
1 |
0 |
0 |
100,8 |
100,9 |
У1=100,85 |
0,005 |
|
|
2 |
0 |
1 |
0 |
85,2 |
85,6 |
У2=85,4 |
0,08 |
|
|
3 |
0 |
0 |
1 |
86,0 |
85,0 |
У3=85,5 |
0,5 max |
|
|
4 |
1/2 |
1/2 |
0 |
88,8 |
89,3 |
У12=89,05 |
0,11 |
|
|
5 |
1/2 |
0 |
1/2 |
90,3 |
90,7 |
У13=90,5 |
0,08 |
|
|
6 |
0 |
1/2 |
1/2 |
85,5 |
85,4 |
У23=85,45 |
0,05 |
|
Додатковіточки |
7 |
0,333 |
0,333 |
0,333 |
88,3 |
88,8 |
У123=88,55 |
0,11 |
|
8 |
0,15 |
0,595 |
0,255 |
86,6 |
86,8 |
У0=86,7 |
0,02 | |
|
9 |
0,3 |
0,49 |
0,21 |
87,6 |
88,1 |
У0=87,85 |
0,11 | |
|
|
|
|
|
|
|
|
|
|
Дисперсія за рядком розраховується за формулою:
 ,
,
де m – число паралельних дослідів у рядку.
Перевіряється однорідність дисперсії виміру функції відгуку по критерію Кохрена.
Опитне значення критерію Кохрена дорівнює
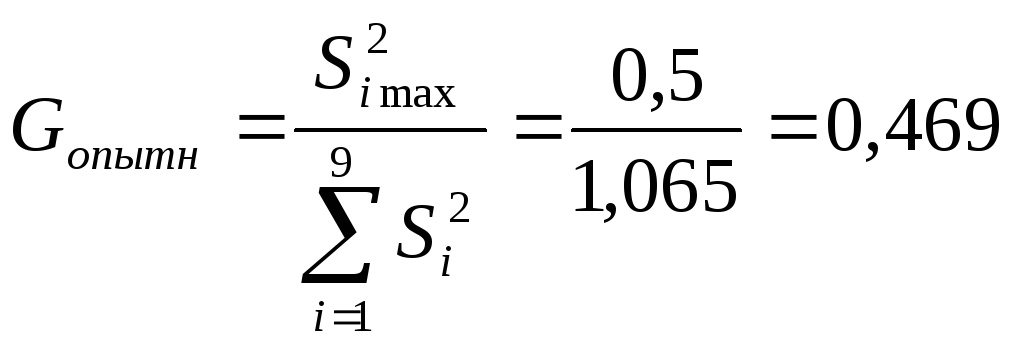 .
.
Вважається, що дисперсії однорідні, якщо опитне значення критерію Кохрена не перевищує табличного.
Табличне значення критерію Кохрена визначають для рівня значущості Р=0,05, числа ступенів свободи К=2-1=1 і N=9.
За таблицею 1
![]() .
.
Оскільки
![]() ,
,
то гіпотеза про однорідність дисперсії не відкидається.
Обчислюються коефіцієнти моделі

Визначається похибка досліду за формулою:
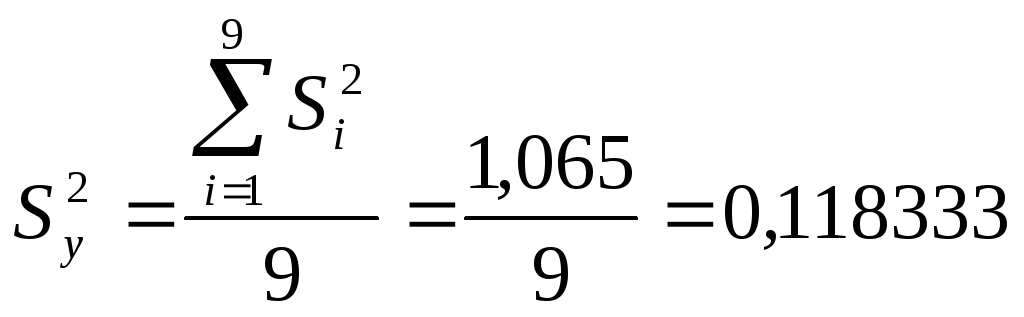
![]() .
.
Оцінюється похибка визначення коефіцієнтів моделі:
![]() .
.
Отже,
коефіцієнт
![]() моделі
є не
значим.
моделі
є не
значим.
Визначається математична модель:
![]() .
.
8. Проводиться оцінка коефіцієнтів моделі.
Оскільки симплекс-решітчасті плани є насиченими, то для оцінки коефіцієнтів моделі використовується критерій Стьюдента.
Для цього до основного плану додається декілька точок у центрі плану. Це точки 7,8 і 9. При цьому, якщо опиниться, що для крапок, поставлених у центрі плану, коефіцієнти моделі значимі, то вважають, що і для всього плану модель адекватна.
Опитне значення критерію Стьюдента для кожної з точок, поставлених в центрі плану, обчислюються за формулою:
![]() ,
,
де
![]() –
відхилення
в центральній точці розрахункового
значення функції відгуку від її
досвідченого значення;
–
відхилення
в центральній точці розрахункового
значення функції відгуку від її
досвідченого значення;
![]()
![]() –число
паралельних дослідів;
–число
паралельних дослідів;
![]() –частина
дисперсій передбаченого значення
функції відгуку, що є функцією тільки
координат точок симплексу, для якої
наперед обчислені значення проекцій
ліній рівного рівня, тобто ізоляції.
–частина
дисперсій передбаченого значення
функції відгуку, що є функцією тільки
координат точок симплексу, для якої
наперед обчислені значення проекцій
ліній рівного рівня, тобто ізоляції.
Відхилення
![]() дорівнюють:
дорівнюють:
для
досліду
№7
![]() =87,5-88,5=-0,97;
=87,5-88,5=-0,97;
для
досліду
№8
![]() =85,88-86,7=-0,82;
=85,88-86,7=-0,82;
для
досліду
№9
![]() =86,99-87,85=-0,86.
=86,99-87,85=-0,86.
У
центральній точці
У=0,628. Тому
![]() .
.
Опитне значення крітерію Стьюдента дорівнює
![]() .
.
9. Визначається табличне значення критерію Стьюдента для Р=0,05 і числа ступенів свободи К2=N-1=9-1=8
![]() .
.
Оскільки
![]() .
.
Аналогічні співвідношення можуть бути одержані для точок №8 і №9.
Відповідно коефіцієнти моделі значимі.
Подальші
дослідження показали, що для опису
зв'язку
![]() потрібно
скористатися моделлю третього порядку.
потрібно
скористатися моделлю третього порядку.
![]() .
.
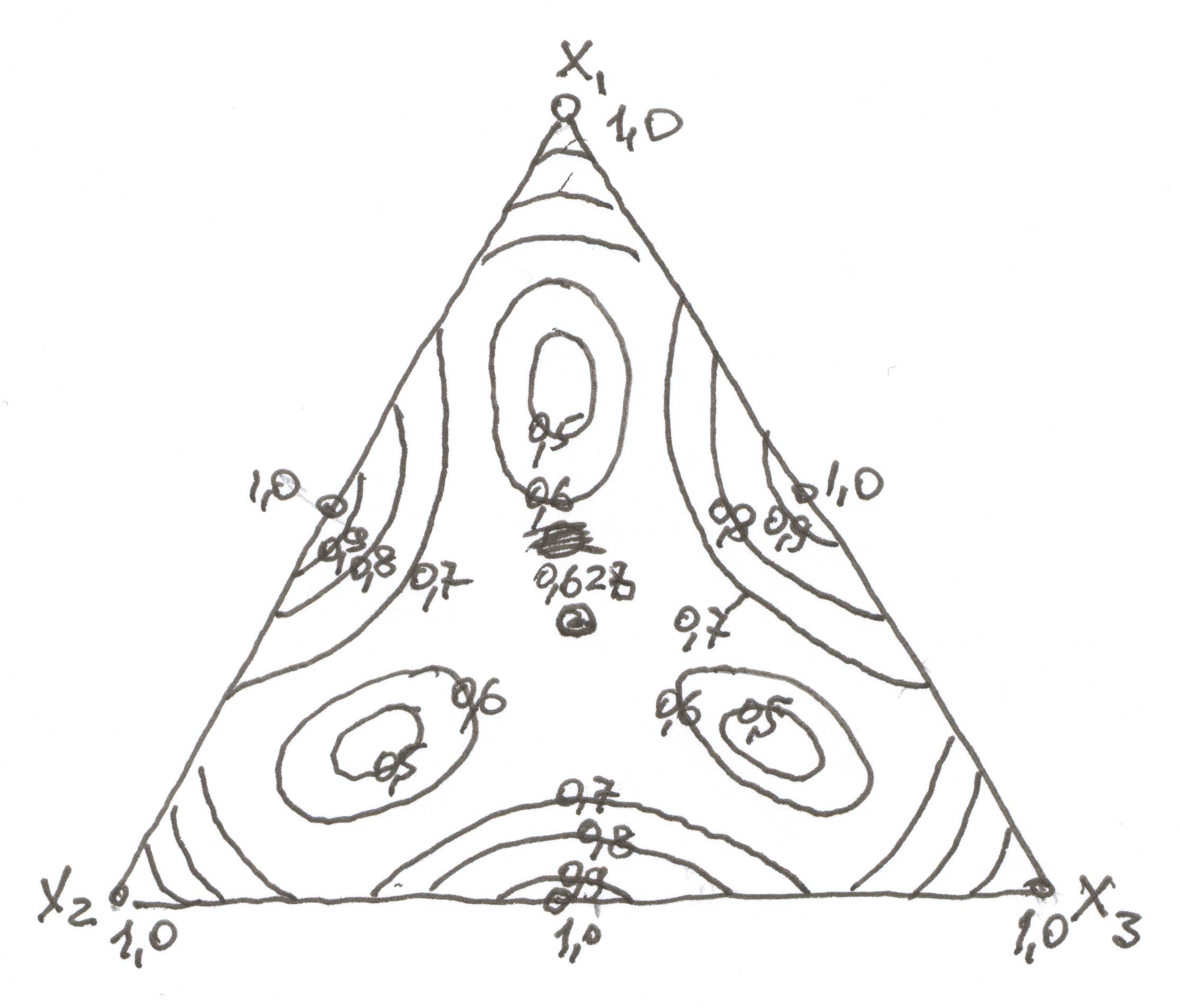
Рис. 3.1 – Лінії рівного рівня (ізолінії) для квадратичної моделі три компонентного складу симплекс-решітчастого плану
