Результати наведені в таблиці 2.1.
Таблиця 2.1
|
№ дсліду |
Х0 |
Х1 |
Х2 |
|
|
|
Узагальн.парам. | |||
|
Натур. |
Умов. |
Натур. |
Умов. |
Натур. |
Умов. | |||||
|
1 |
+ |
- |
- |
8 |
1 |
90 |
1 |
1,1 |
1 |
|
|
2 |
+ |
+ |
- |
10 |
1 |
80 |
1 |
1,5 |
1 |
|
|
3 |
+ |
- |
+ |
24 |
1 |
70 |
1 |
2,6 |
1 |
|
|
4 |
+ |
+ |
+ |
36 |
1 |
60 |
0 |
0,7 |
0 |
|
Далі обчислюється коефіцієнт моделі
.
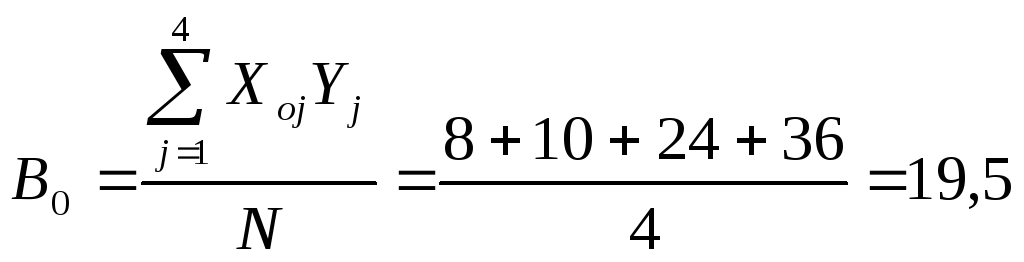
Тому модель першого параметра оптимізації
Для другого приватного параметра
Для третього приватного параметра
Для узагальненого параметра оптимізації, що дорівнює середньому геометричному, коефіцієнт моделі складають
,
|
|
.
Другий спосіб
Вагові коефіцієнти визначаються експертами.
Визначення узагальненого параметра проводять за формулою:
де
– вагові
коефіцієнти;
–
альтернативні
обмеження за кожним з приватних
параметрів.
Припустимо, що внаслідок експертних оцінок одержано:
,
для першого рядка матриці планування (таблиця 1) одержимо.
Аналогічно для досліджуючих рядків
.
Коефіцієнти моделі для узагальненого параметра.
.
Тому
Третій спосіб
Використання шкали бажаності.
Кожному з параметрів оптимізації відповідає шкала, що назівається шкалою бажаності «градації».
Ця шкала встановлює залежність між вихідними значеннями приватного параметра оптимізації та якісною оцінкою цієї величини.
Шкала бажаності має безрозмірний вигляд:
|
Дуже добре (відмінно) |
1,00 – 0,80 |
|
Добре |
0,80 – 0,63 |
|
Задовільно |
0,63 – 0,37 |
|
Погано |
0,37 – 0,20 |
|
Дуже погано |
0,20 – 0,00 |
Шкали бажаності обмежують зліва показником 0,37, а справа – 0,8.
За початок звіту приймають точки, що відповідає шкалі градації 0,37.
Кінцем служить крапка 0,8 на шкалі.
Інтервал між 0,37 – 0,8 поділяють для кожного з приватних параметрів пропорційно фізичній сутності кожного із вказаних параметрів. Привид решти точок відповідно до шкали градації вимагає від експериментатора значення сутності цього явища й обережності.
Розглянемо порядок приведення досвідчених крапок у відповідність з школою градації на прикладі таблиці 3.2.
Каждому значению опытной точки приписывается значение показателя на шкале желательности.
Таблиця2.2
|
№ опыта |
|
|
|
Узагальненийпараметр | |||
|
Натур |
Умов. |
Натур |
Умов. |
Натур |
Умов. | ||
|
1 |
8 |
0,37 |
90 |
0,78 |
1,1 |
0,39 |
|
|
2 |
10 |
0,50 |
80 |
0,63 |
1,5 |
0,50 |
|
|
3 |
24 |
0,64 |
70 |
0,50 |
2,6 |
0,78 |
|
|
4 |
36 |
0,78 |
60 |
0,00 |
0,7 |
0,00 |
|
Визначаємо коефіцієнти моделі для узагальненого параметра оптимізації.
Аналітично графік функції бажаності виражається за допомогою наступної залежності:
.
Коли х=0 отримуємо:
лівий
кінець шкали бажано 
;
правий
кінець шкали бажано
.