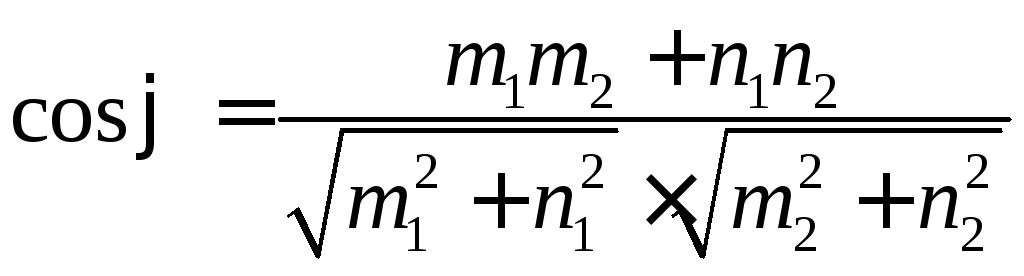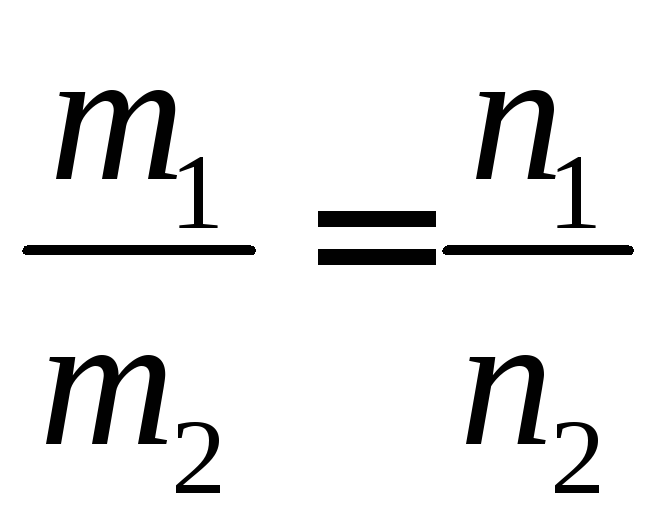3.3. Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых

Способ задания прямых	Угол между двумя прямыми	Условия параллельности	Условия перпендику-лярности
Прямые заданы общими уравнениями: , .
Прямые заданы каноническими уравнениями: , .
Прямые заданы уравнениями с угловым коэффициентом: ,

3.4. Задание плоскости в пространстве

Плоскость в пространстве может быть задана:

1. тремя точками плоскости;

2. точкой и нормальным вектором плоскости, тогда множество точек М плоскости, проходящей через точку М₀ ортогонально вектору , будет удовлетворять условию.

3. точкой и двумя неколлинеарным векторам ,, тогда множество точекМ плоскости будет удовлетворять условию, что векторы ,,компланарны

3.5. Виды уравнений плоскости

1. Общее уравнение плоскости:

Ах+By+Cz+D=0,

где (A;B;C) – нормальный вектор плоскости.

2) Уравнение плоскости, проходящей через точку М₀ параллельно

двум неколлинеарным векторам (m₁;n₁;p₁), (m₂;n₂;p₂).

.

2. Уравнение плоскости, проходящей через три точки

М₁(x₁;y₁;z₁), M₂(x₂;y₂;z₂), M₃(x₃,y₃,z₃):

.

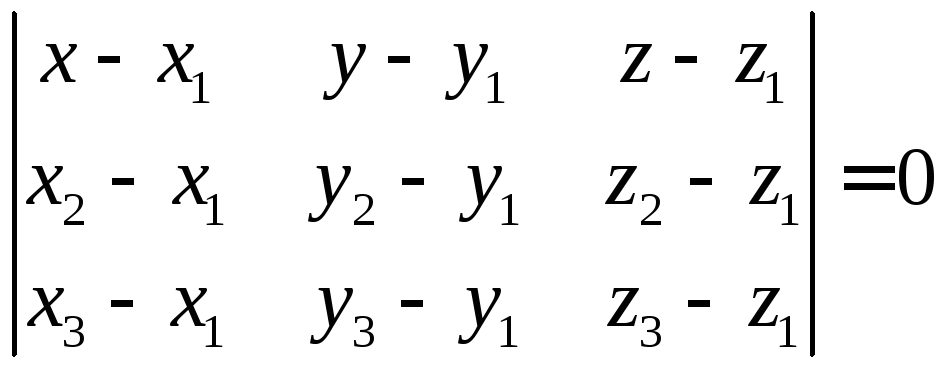Это уравнение есть условие компланарности трех векторов .

3.6. Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей

Пусть две плоскости ₁ и ₂ заданы общими уравнениями:

₁: A₁x+B₁y+C₁z+D=0;

₂: A₂x+B₂y+C₂z+D=0.

Вопрос об определении угла между указанными плоскостями сводится к определению угла  между их нормальными векторами (А₁,В₁,С₁) и (А₂,В₂,С₂).

Из определения скалярного произведения и записи его в координатной форме, получим:

.

Условие параллельности плоскостей ₁ и ₂, эквивалентное условию коллинеарности векторов (А₁,В₁,С₁) и (А₂,В₂,С₂), заключается в пропорциональности координат этих векторов, т.е. имеет вид:

.

Условие перпендикулярности плоскостей ₁ и ₂ выражается равенством нулю скалярного произведения векторов (А₁,В₁,С₁) и (А₂,В₂,С₂). Оно имеет вид:

А₁А₂+В₁В₂+С₁С₂=0.

3.7. Определение прямой в пространстве

Прямая в пространстве может быть задана как линия пересечения двух плоскостей; либо точкой и направляющим вектором прямой.

Прямая в пространствене определяется через нормальный вектор, т.к. любая прямая имеет в каждой своей точке бесконечное множество нормальных векторов.

3.8. Виды уравнений прямой в пространстве

1) Каноническое уравнение прямой:

,

где (m;n;p) – направляющий вектор прямой; - координаты заданной точки прямой.

2) Уравнение прямой, проходящей через две точки М₁(х₁;у₁;z₁) и М₂(х₂;у₂;z₂):

.

3) Общее уравнение прямой в пространстве:

Каждое из уравнений системы является уравнением плоскости, прямая – линия пересечения двух плоскостей.

4) Параметрическое уравнение прямой:

,

где m, n, p – координаты направляющего вектора прямой;- координаты заданной точки прямой,t – параметр, -t+.

3.9. Угол между прямыми в пространстве. Условия параллельности и перпендикулярности прямых

Пусть две прямые в пространстве заданы своими каноническими уравнениями:

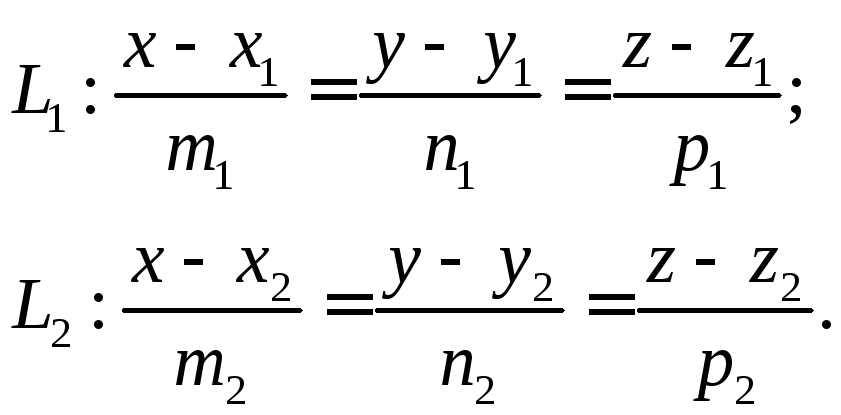
Задача определения угла между этими прямыми сводится к определению угла  между их направляющими векторами (m₁;n₁;p₁) и (m₂;n₂;p₂). По определению скалярного произведения:

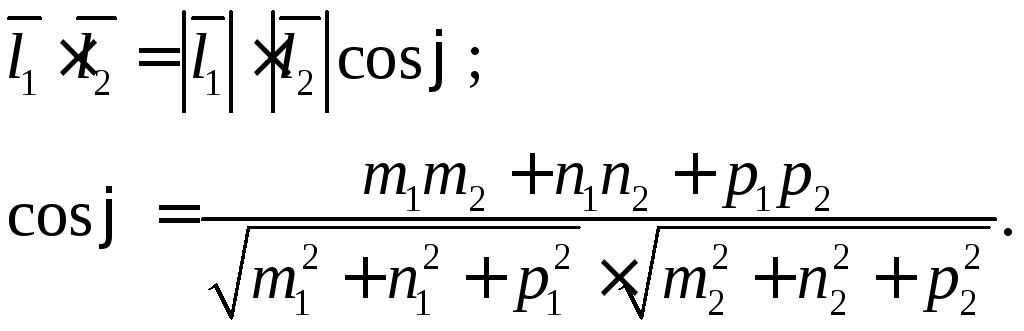
Условие параллельности прямых L₁ и L₂, эквивалентное условию коллинарности векторов (m₁;n₁;p₁) и (m₂;n₂;p₂), заключается в пропорциональности координат их направляющих векторов:

Условие перпендикулярности прямых L₁ и L₂ выражается равенством нулю скалярного произведения векторов и:

m₁m₂+n₁n₂+p₁p₂=0.