
- •Федеральное агентство по образованию Российской Федерации
- •Введение
- •1. Матрицы и определители
- •1.1. Понятие матрицы
- •1.2. Алгебраические операции над матрицами
- •1.3.5. Свойства определителей
- •1.4. Обратная матрица
- •1.4.1. Определение обратной матрицы
- •1.4.2. Методы вычисления обратной матрицы
- •3) Составляем матрицу алгебраических дополнений:
- •1.5. Ранг матрицы
- •1.5.1. Определение ранга матрицы
- •1.5.2. Методы вычисления ранга матрицы
- •1.6. Системы линейных уравнений
- •1.6.1. Определение системы
- •1.6.2. Классификация систем
- •1.6.3. Крамеровские системы
- •1.6.4. Произвольные неоднородные системы
- •1.6.6. Метод Гаусса решения систем неоднородных уравнений
- •2. Векторная алгебра
- •2.1. Понятие вектора
- •2.2. Линейные операции над векторами
- •2. 3. Проекция вектора на ось
- •2.4. Линейная зависимость векторов
- •2.5. Базис. Координаты вектора
- •2.6. Прямоугольная (декартова) система координат
- •2.7. Скалярное произведение векторов
- •2.8. Векторное произведение векторов
- •2.9. Смешанное произведение векторов
- •3. Прямые и плоскости
- •3.1. Задание прямой на плоскости
- •3.2. Виды уравнений прямой на плоскости
- •3.3. Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых
- •3.4. Задание плоскости в пространстве
- •3.5. Виды уравнений плоскости
- •3.6. Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей
- •3.7. Определение прямой в пространстве
- •3.8. Виды уравнений прямой в пространстве
- •3.9. Угол между прямыми в пространстве. Условия параллельности и перпендикулярности прямых
- •3.10. Условие принадлежности прямых одной плоскости
- •3.11. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости
- •4.2. Гипербола
- •4.3. Парабола
- •Вариант №0
- •2. Вычислить определитель
- •Решение варианта №0
- •2. Вычислить определитель
- •Рекомендуемая литература
- •164500, Г. Северодвинск, ул. Воронина, 6.
4.2. Гипербола
Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек плоскости F1 и F2, называемых фокусами, есть величина постоянная, равная 2а.
 Точки
F1
и F2
имеют координаты F1(c,0)
и F2(-c,0).
Точки
F1
и F2
имеют координаты F1(c,0)
и F2(-c,0).
Пусть точка М(х,у) – некоторая точка плоскости. Обозначим через r1 и r2 расстояния от точки М до точек F1 и F2 соответственно. Согласно определению гиперболы равенство:
|r1-r2|=2a
является необходимым и достаточным условием расположения точки М(х,у) на данной гиперболе.
Уравнение гиперболы в данной системе координат примет вид:
 - каноническое
уравнение
гиперболы,
- каноническое
уравнение
гиперболы,
где b2=c2-a2.
Если а=b, то гипербола называется равносторонней.
Свойства гиперболы.
Гипербола симметрична относительно осей Ох и Оу и точки О(0;0) – центра гиперболы.
Гипербола состоит из двух частей, называемых ветвями гиперболы.
Точки пересечения гиперболы с осью Ох А1(а;0) и А2(-а;0) называются вершинами гиперболы.
Отрезок А1А2=2а называется действительной осью гиперболы.
3)
Прямые
![]() и
и![]() называютсяасимптотами
гиперболы
(ветви
гиперболы неограниченно приближаются
к этим прямым).
называютсяасимптотами
гиперболы
(ветви
гиперболы неограниченно приближаются
к этим прямым).
Отношение расстояния между фокусами к длине действительной оси эллипса называется эксцентриситетом гиперболы:
е=с/а.
Учитывая, что b2=с2-а2, получим:
 .
.
Из этой формулы видно, что эксцентриситет гиперболы больше единицы.
Эксцентриситет
гиперболы можно рассматривать как
числовую характеристику величины угла
между ее асимптотами, т.к. отношение
![]() есть тангенс половины угла между
асимптотами гиперболы.
есть тангенс половины угла между
асимптотами гиперболы.
4.3. Парабола
Параболой называется множество точек плоскости, каждая из которых одинаково удалена от данной точки F, называемой фокусом, и данной прямой l, называемой директрисой.
Расстояние от фокуса F до директрисы l называется параметром параболы и обозначается через р.
Пусть ось Ох проходит через фокус F перпендикулярно директрисе, а начало координат расположено посередине между фокусом и директрисой. Тогда F(p/2;0), а уравнение директрисы х=-р\2.
у2=2рх
– каноническое уравнение параболы.

Свойства параболы.
1) Парабола симметрична относительно оси Ох (Ох - ось симметрии параболы), т.к. в каноническом уравнении параболы величина у фигурирует в четной степени.
Парабола проходит через начало координат, точка О(0;0) – вершина параболы.
Отметим, что кривая у2=2рх при р<0 также является параболой, которая располагается в левой полуплоскости.
Пример контрольной работы и образец ее выполнения.
Вариант №0
1. Вычислить произведение матриц
 .
.
2. Вычислить определитель
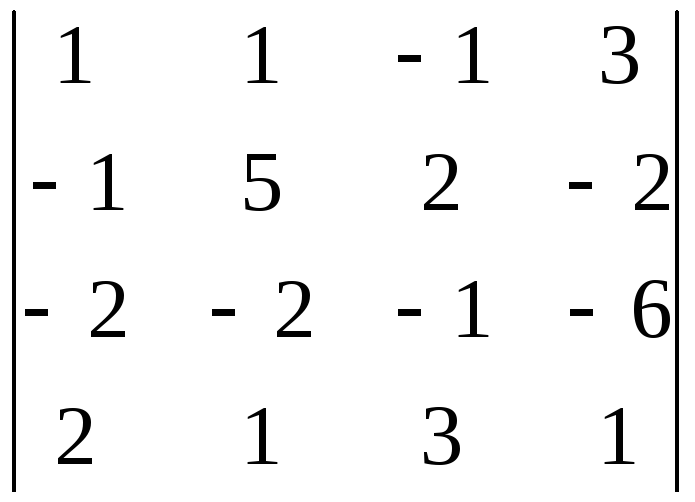 .
.
3. Найти обратную матрицу
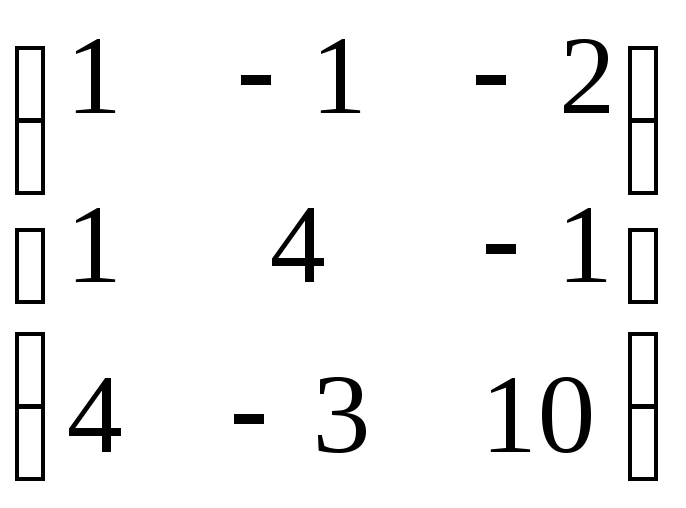 .
.
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
б) Методом Крамера.
в) Методом Гаусса.
а)
 б)
б) в)
в)
5.
Написать разложение вектора
![]() по базису
по базису![]() :
:
![]() .
.
6.
Установить, являются ли векторы
![]() линейно-зависимыми:
линейно-зависимыми:
![]() .
.
7.
Найти площадь параллелограмма,
построенного на векторах
![]() и
и![]() :
:
![]() .
.
8. Составить уравнение прямой, проходящей через две точки М1(1, 5), М2(3, 3) и найти расстояние от точки Р(1,-2) до полученной прямой.
9. Найти угол между прямыми:
![]() .
.
10. От общего уравнения прямой

перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
![]() .
.
12. Найти расстояние от точки М до плоскости :
![]() .
.
13. Найти проекцию точки М на плоскость :
![]() .
.
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
![]() .
.
