
- •Федеральное агентство по образованию Российской Федерации
- •Введение
- •1. Матрицы и определители
- •1.1. Понятие матрицы
- •1.2. Алгебраические операции над матрицами
- •1.3.5. Свойства определителей
- •1.4. Обратная матрица
- •1.4.1. Определение обратной матрицы
- •1.4.2. Методы вычисления обратной матрицы
- •3) Составляем матрицу алгебраических дополнений:
- •1.5. Ранг матрицы
- •1.5.1. Определение ранга матрицы
- •1.5.2. Методы вычисления ранга матрицы
- •1.6. Системы линейных уравнений
- •1.6.1. Определение системы
- •1.6.2. Классификация систем
- •1.6.3. Крамеровские системы
- •1.6.4. Произвольные неоднородные системы
- •1.6.6. Метод Гаусса решения систем неоднородных уравнений
- •2. Векторная алгебра
- •2.1. Понятие вектора
- •2.2. Линейные операции над векторами
- •2. 3. Проекция вектора на ось
- •2.4. Линейная зависимость векторов
- •2.5. Базис. Координаты вектора
- •2.6. Прямоугольная (декартова) система координат
- •2.7. Скалярное произведение векторов
- •2.8. Векторное произведение векторов
- •2.9. Смешанное произведение векторов
- •3. Прямые и плоскости
- •3.1. Задание прямой на плоскости
- •3.2. Виды уравнений прямой на плоскости
- •3.3. Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых
- •3.4. Задание плоскости в пространстве
- •3.5. Виды уравнений плоскости
- •3.6. Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей
- •3.7. Определение прямой в пространстве
- •3.8. Виды уравнений прямой в пространстве
- •3.9. Угол между прямыми в пространстве. Условия параллельности и перпендикулярности прямых
- •3.10. Условие принадлежности прямых одной плоскости
- •3.11. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости
- •4.2. Гипербола
- •4.3. Парабола
- •Вариант №0
- •2. Вычислить определитель
- •Решение варианта №0
- •2. Вычислить определитель
- •Рекомендуемая литература
- •164500, Г. Северодвинск, ул. Воронина, 6.
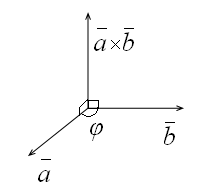
2.8. Векторное произведение векторов
Векторным
произведением
векторов
![]() и
и![]() называется вектор
называется вектор![]() ,
удовлетворяющий следующим условиям:
,
удовлетворяющий следующим условиям:
1)
![]() ; (2)
; (2)
2)
![]() ;
;
3) тройка векторов
![]() ,
,![]() ,
,![]() - правая (кратчайший поворот от вектора
к вектору происходит против часовой
стрелки).
- правая (кратчайший поворот от вектора
к вектору происходит против часовой
стрелки).
Алгебраические свойства векторного произведения:
1)
![]() - свойствоантикоммутативности;
- свойствоантикоммутативности;
2) (![]() )
)![]() =(
=(![]() )
– свойство ассоциативности;
)
– свойство ассоциативности;
3)
![]() - векторное произведение вектора на
себя равно нулю.
- векторное произведение вектора на
себя равно нулю.
Геометрические свойства векторного произведения:
1) вектора
![]() и
и![]() коллинеарны, если
коллинеарны, если![]() =0;
=0;
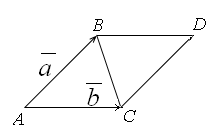
2) модуль векторного
произведения |![]()
![]() |
равен площадиS
параллелограмма, построенного на
приведенных к общему началу векторах
|
равен площадиS
параллелограмма, построенного на
приведенных к общему началу векторах
![]() и
и![]() -геометрический
смысл
векторного произведения.
-геометрический
смысл
векторного произведения.
Векторное
произведение в координатах векторов
![]() (ха;
уа;
zа)
и
(ха;
уа;
zа)
и
![]() (хb;
уb;
zb)
есть вектор, вычисляемый по правилу:
(хb;
уb;
zb)
есть вектор, вычисляемый по правилу:
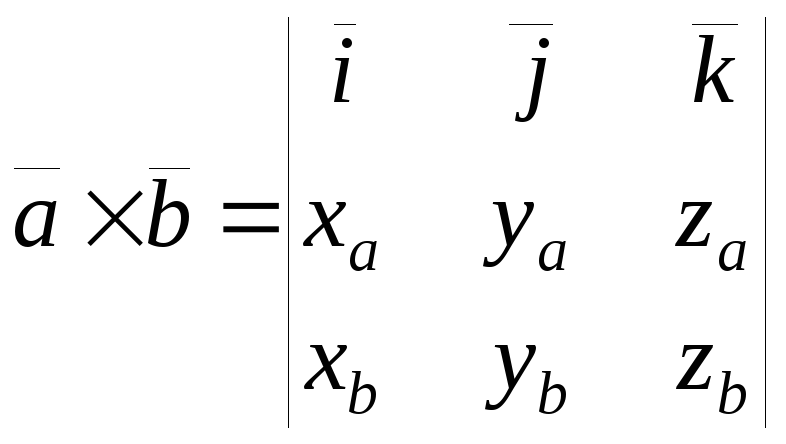 .
.
Из определения векторного произведения вытекают следующие формулы:
- синус
угла между
векторами
![]() ;
;
- площадь
треугольника,
построенного на векторах
![]() и
и![]() ,
равна 1/2|
,
равна 1/2|![]()
![]() |.
|.
2.9. Смешанное произведение векторов
Смешанным
произведением
упорядоченной тройки векторов
![]() называется число, равное скалярному
произведению вектора
называется число, равное скалярному
произведению вектора![]() на вектор
на вектор![]() :
:
![]() .
.
Алгебраические свойства смешанного произведения:
1)
![]() - смешанное произведение не изменяется
от перегруппировки сомножителей;
- смешанное произведение не изменяется
от перегруппировки сомножителей;
2)
![]() -
смешанное произведение меняет знак на
обратный при перестановке пары
сомножителей;
-
смешанное произведение меняет знак на
обратный при перестановке пары
сомножителей;
3)
![]() - при умножении вектора на число смешанное
произведение умножается на это число.
- при умножении вектора на число смешанное
произведение умножается на это число.
Геометрические свойства смешанного произведения:
1) три вектора
![]() компланарны, если
компланарны, если![]() -условие
компланарности
трех векторов;
-условие
компланарности
трех векторов;
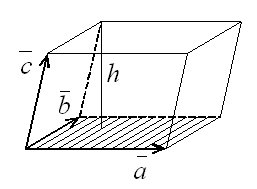
2) модуль смешанного
произведения ![]()
некомпланарных векторов равен объему
параллелепипеда, построенного на
приведенных к общему началу векторах
некомпланарных векторов равен объему
параллелепипеда, построенного на
приведенных к общему началу векторах
![]() ,
,![]() и
и![]() ;
;
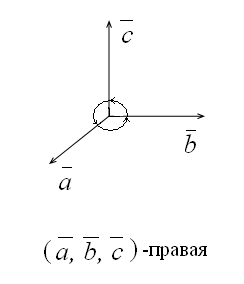
3) тройка векторов
правая, если (![]() ,
,![]() ,
,![]() )0;
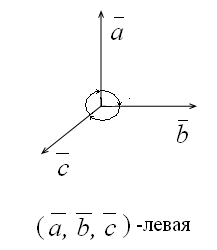
тройка левая, если (
)0;
тройка левая, если (![]() ,
,![]() ,
,![]() )0.
)0.
Смешанное
произведение в координатах
трех векторов
![]() ,
,![]() ,
,![]() есть число, равное определителю,
составленному из координат векторов:
есть число, равное определителю,
составленному из координат векторов:
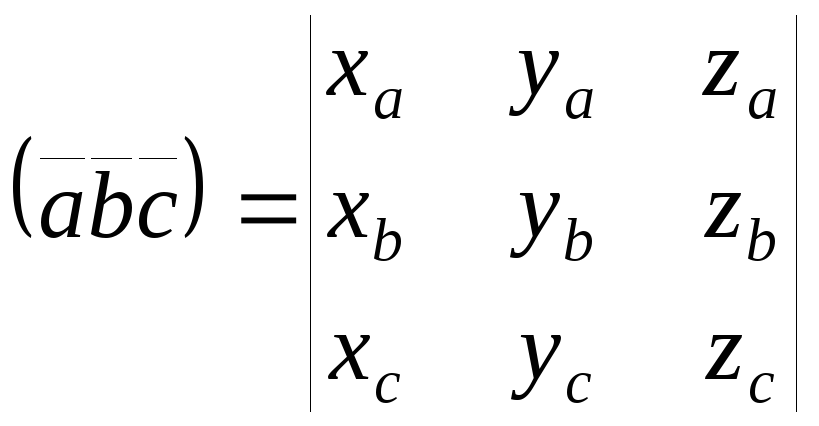 .
.
Из определения смешанного произведения векторов вытекают следующие формулы:
- объем тетраэдра
![]() ;
;
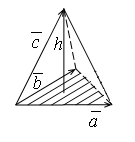
- высота тетраэдра
(параллелепипеда)
![]() .
.
3. Прямые и плоскости
3.1. Задание прямой на плоскости
В сякий
вектор
сякий
вектор![]() ,
параллельный прямойL,
называется направляющим
вектором прямой
L.
,
параллельный прямойL,
называется направляющим
вектором прямой
L.
Всякий вектор
![]() ,
ортогональный прямойL,
называется нормальным
вектором прямой
L.
,
ортогональный прямойL,
называется нормальным
вектором прямой
L.
Прямая на плоскости задается:
парой точек этой прямой;
точкой и направляющим вектором прямой, тогда множество точек М прямой, проходящей через точку М0 параллельно вектору
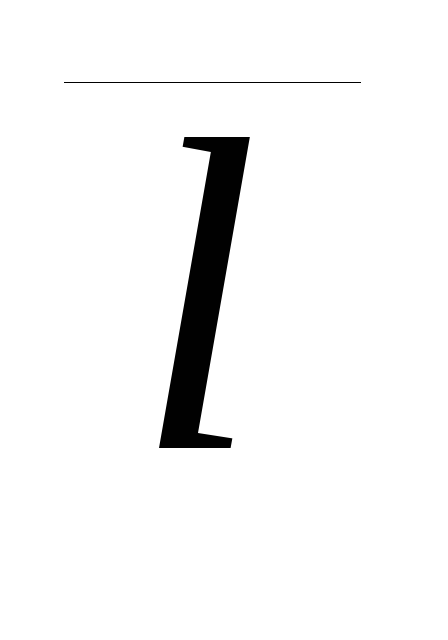 ,
будет удовлетворять условию
,
будет удовлетворять условию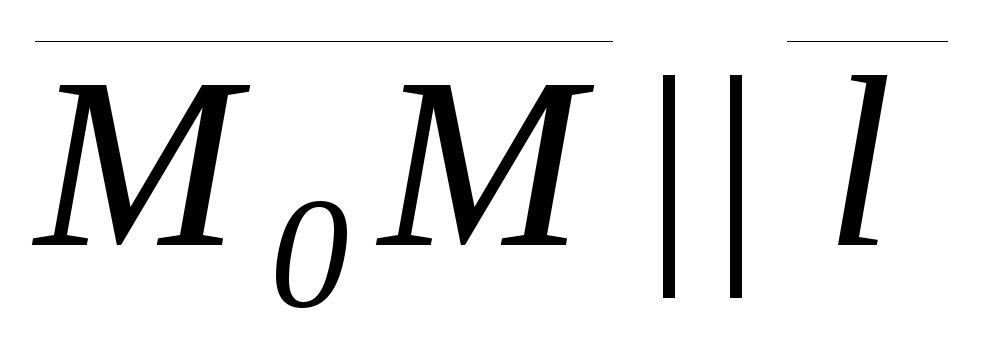 .
.точкой и нормальным вектором прямой, тогда множество точек М прямой, проходящей через точку М0 ортогонально вектору
 ,
будет удовлетворять условию
,
будет удовлетворять условию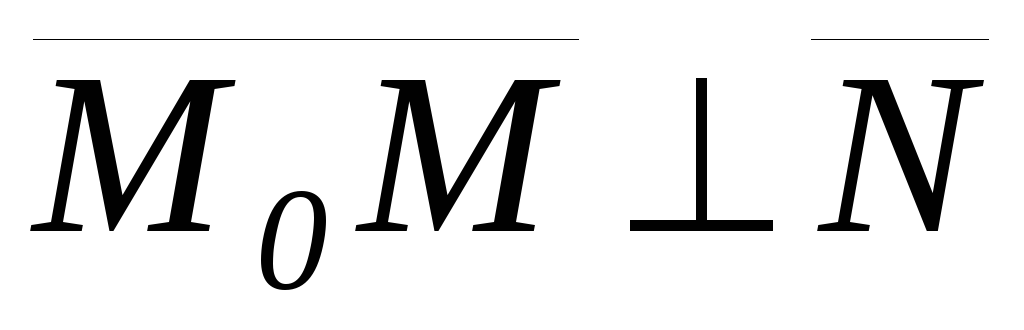 .
.
3.2. Виды уравнений прямой на плоскости
1) Общее уравнение прямой:
Ах+Ву+С=0,
где
![]() (А;В)
– нормальный вектор прямой L.
(А;В)
– нормальный вектор прямой L.
2) Каноническое уравнение прямой:
![]() ,
,
где
![]() (m;n)
– направляющий вектор прямой L.
(m;n)
– направляющий вектор прямой L.
3) Уравнение прямой, проходящей через две точки М1(х1;у1) и М2(х2;у2):
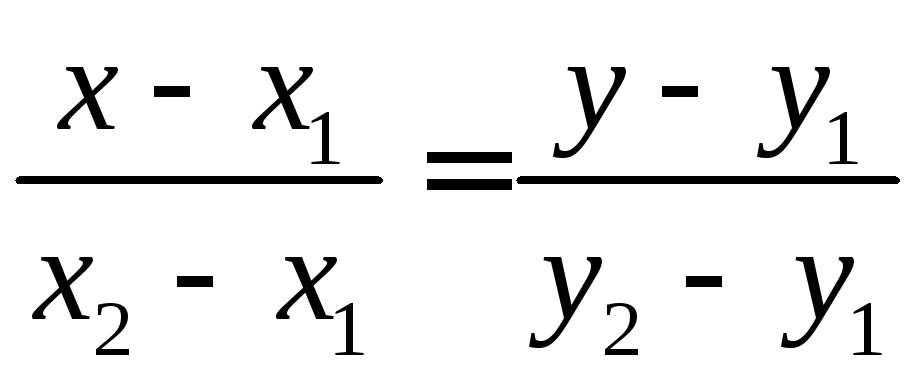 .
.
4) Параметрическое уравнение прямой:
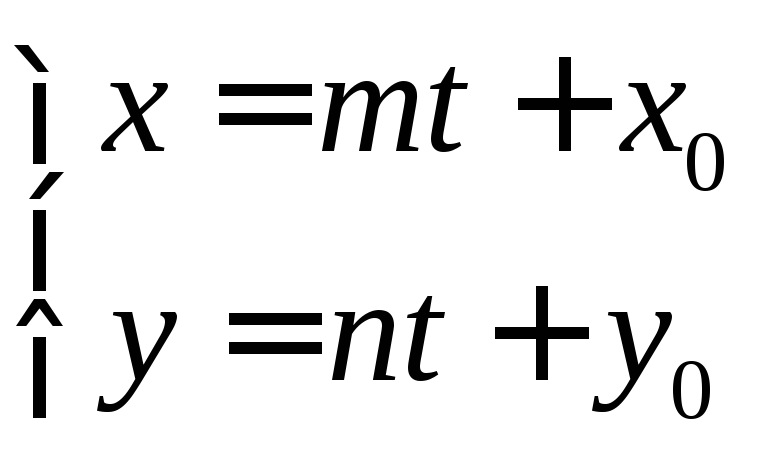 ,
,
где m,
n,
– координаты
направляющего вектора
![]() прямой;
прямой;![]() - координаты заданной точки прямой,t
– параметр,
-t+.
- координаты заданной точки прямой,t
– параметр,
-t+.
5) Уравнение прямой с угловым коэффициентом:
у=kх+b,
где k=tg - угловой коэффициент прямой L (тангенс угла наклона прямой к оси Ох).
