4.2. Деякі задачі, що приводять до кривих другого порядку

Задача. Знайти геометричне місце точок на площині xOy, які задовольняють наступній властивості: відношення відстаней від довільної точки М цієї множини до точки F(2; 1) і від точки М до прямої х = 4 є величина стала, що дорівнює ε. Розглянути випадки: 1) ε = 1/2; 2) ε = 1; 3) ε = 2.

Рис. 23

Розв’язання. Покажемо, що при будь-якому значенні ε шукане геометричне місце точок є кривою другого порядку, тип якої істотно залежить від величини ε (ε < 1  еліпс, ε = 1  парабола, ε > 1  гіпербола).

,,

FM ²=²MK²,

,

,

. (39)

Випадок 1:ε = 1/2.,

,

,.

Зробимо заміну змінних x=x4/3,y =y1 і введемо нову систему координатxOyіз центромO(4/3; 1), що виходить ізxOy паралельним переносом. У системі координатxOyрівняння кривої набуде вигляду

. (40)

Зауваження.Рівняння (40) являє собою на площині криву другого порядку, називануеліпсом. Для будь-якого еліпса на площині завжди можна ввести таку систему координатOxy, у якій його рівняння матиме вигляд:

. (41)

Випадок 2:ε= 1. З рівняння (39) одержуємо:

,,.

Зробимо заміну змінних x=x3,y =y1. У системі координатxOyмаємо:

. (42)

Зауваження.Рівняння (42) являє собою на площиніxOyкриву другого порядку, називанупараболою. Для будь-якої параболи на площині завжди можна ввести таку систему координатxOy, у якій її рівняння матиме вигляд:

. (43)

Випадок 3: = 2. З рівняння (39) одержуємо:

,,

,

Зробимо заміну змінних x=x14/3,y =y1. У системі координатxOyрівняння кривої набуде вигляду:

(44)

Зауваження.Рівняння (44) являє собою на площині криву другого порядку, називанугіперболою. Для будь-якої гіперболи на площині завжди можна ввести таку систему координатxOy, у якій її рівняння матиме вигляд:

. (45)

4.3. Криві другого порядку. Узагальнення

Кривою другого порядку називається геометричне місце точок на площині, що задовольняє наступній властивості: відношення відстаней від довільної точки М кривої до фіксованої точки F площини (фокус кривої) і від точки М до фіксованої прямої на площині (директриса кривої) є величиною сталою, яка дорівнює ε (ексцентриситет кривої).

Тип кривої другого порядку залежить від величини ε. Крива другого порядку є:

1. еліпс, якщо ε< 1;

2. парабола, якщо ε= 1;

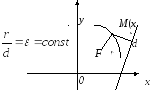3. гіпербола, якщоε> 1.

Рис. 24

Кривою другого порядку є алгебраїчна лінія другого порядку, що визначається рівнянням (38). При переході від однієї системи координат до іншої рівняння кривої змінюватиметься. Найбільш просте рівняння крива другого порядку матиме в канонічній системі координат, одна з осей якої спрямована уздовж перпендикуляра, опущеного з фокусаFна директрису, а інша – паралельно директрисі. Рівняння кривої другого порядку в канонічній системі координат називаєтьсяканонічним рівнянням кривої. Будь-яке рівняння (38) можна звести до канонічного вигляду за допомогою паралельного переносу й повороту системи координат на кут, що визначається з рівняння.

Далі розглядатимемо криві другого порядку в канонічних системах координат.

4.4. Еліпс

Рівняння еліпса в параметричній формі:

0t2. (46)

З рівняння (46) маємо: x/a= cost,y/b= sint. Піднесемо до квадрата і складемо:

(47)

• канонічне рівняння еліпса.

При y= 0 маємох=а; прих= 0у=b, тобто еліпс відсікає на осіОхвідрізкиа, на осіОувідрізки b(рис. 25). Точки перетину еліпса з осями координат називаютьсявершинами еліпса.

Рис. 25. Еліпс (a b) Рис. 26. Еліпс (ab)

Точки F₂(c;0),F₁(c;0), де(ab) називаютьсяфокусамиеліпса.

Величина ε = c/a називається ексцентриситетом еліпса (0   <1). Від ексцентриситету залежить форма еліпса. Якщо ε = 0, то еліпс перетворюється в коло. При ε→1 еліпс вироджується у відрізок [ a; a].

Прямі x=a/називаютьсядиректрисамиеліпса.

Якщо r– відстань від точкиМдо фокуса,d– відстань від точкиМдо найближчої директриси, тоr/d=.

Відстані r₁=F₁M іr₂=F₂Mвід довільної точкиМ(x;y) еліпса до фокусів називаютьсяфокальними радіусамиеліпса.

Знайдемо фокальні радіуси:

Аналогічно .

Таким чином

,(48)

З формул (48) випливає основна властивість еліпса: сума відстаней від будь-якої точки еліпса до фокусів дорівнює 2а.

F₁M + F₂M = 2а.(49)

Зауваження 1. Якщоa<b, то фокуси еліпса мають координатиF₂(0;c),F₁(0;c), де. Ексцентриситет еліпса=с/b, директриси еліпса y=b/(рис. 26).

Зауваження 2. Відомо, що фокальні радіусиF₁MіF₂Mперетинають дотичну до еліпса в точціМпід однаковими кутами. Отже, промінь світла, або звукова хвиля, що виходить із фокусаF₁, відбившись від еліпса, потрапить у фокусF₂(оптична властивістьеліпса).

Зауваження 3. Якщоa=b=R, то еліпс вироджується в коло радіусаR; фокуси F₁ і F₂збігаються з центромOкола, ексцентриситет кола= 0 (рис. 27). Коло директрис не має.

Коло– геометричне місце точок на площині, рівновіддалених від даної фіксованої точки, яка називаєтьсяцентром кола.

Рис. 27. Коло

Приклад 11.Звести до канонічного вигляду рівняння

9x²+ 25y²36x + 50y = 164. Визначити тип кривої, зробити креслення.

Розв’язання.Виділимо в рівнянні лінії повні квадрати:

, ,,, де

В системі координат xOyотримане канонічне рівняння еліпса. Центр еліпса має координатиO(2;1). Півосі еліпсаa= 5,b= 3.=c/a= 4/5.

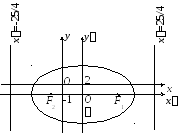
Рис. 28