
- •Метод гаусса решения систем линейных уравнений и его модификации
- •Кафедра: «Математического анализа»
- •Введение
- •Компактная схема Гаусса
- •Компактная схема Гаусса
- •Порядок заполнения таблицы (прямой ход):
- •Обратный ход:
- •Модификация Краута – Дулитла
- •Порядок заполнения таблицы, прямой ход:
- •3. Схема Гаусса с выбором главного элемента
- •Задания к лабораторной работе по теме «Решение систем линейных уравнений»
- •Тесты для защиты лабораторной работы Вариант № 1
- •Вариант № 2
- •Вариант № 3
- •1. Последние строки разделов и всех столбцов, кромеи, это результат:
- •Список литературы
- •Михащенко Татьяна Николаевна Метод гаусса и его модификации
- •640669, Г. Курган, ул. Гоголя, 25
Порядок заполнения таблицы (прямой ход):
Записываем коэффициенты системы в четырёх строках и пяти столбцах раздела I (табл. 1).
Суммируем все коэффициенты по строке и записываем сумму в столбце
 столбец
контроля), т.е.a16=
столбец
контроля), т.е.a16= .
.Делим все числа, стоящие в первой строке, на ведущий элемент a11
 и результаты b1j=a1j
/a11
записываем в пятой строке раздела I.
и результаты b1j=a1j
/a11
записываем в пятой строке раздела I.Вычисляем
 и делаем проверку. Если вычисления
ведутся постоянным знаком после запятой,
то числаb16
и
и делаем проверку. Если вычисления
ведутся постоянным знаком после запятой,
то числаb16
и
 не должны отличаться более чем на
единицу последнего разряда. В противном
случае следует проверить действия
пункта 3.
не должны отличаться более чем на
единицу последнего разряда. В противном
случае следует проверить действия
пункта 3.
Вычисляем коэффициенты a
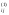 (i
=2,3,4; j=2,3,4,5,6)
по формуле
(i
=2,3,4; j=2,3,4,5,6)
по формуле
a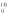 =aij–ai1b1j.
Результаты
записываем в первые три строки раздела
II.
=aij–ai1b1j.
Результаты
записываем в первые три строки раздела
II.
Осуществляем контроль. Сумма элементов каждой строки
 (i=2,3,4)
не должна отличаться от a
(i=2,3,4)
не должна отличаться от a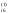 более чем на единицу последнего разряда.
более чем на единицу последнего разряда.Делим все элементы первой строки раздела II на a

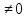 ,
результаты записываем в четвёртой
строке раздела II.
Осуществляем контроль.
,
результаты записываем в четвёртой
строке раздела II.
Осуществляем контроль.Вычисляем a
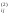 ,
a
,
a =a
=a –a
–a b
b ,
(i=3,4;
j=3,4,5,6).
Осуществляем
контроль.
,
(i=3,4;
j=3,4,5,6).
Осуществляем
контроль.Делим элементы первой строки раздела III на a
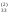 и находим числа
b
и находим числа
b =a
=a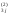 /a
/a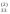 .
Все результаты записываем в третьей
строке раздела
III.
Осуществляем контроль.
.
Все результаты записываем в третьей
строке раздела
III.
Осуществляем контроль.Вычисляем a
 =a
=a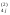 - a
- a b
b .
Результаты
записываем в разделе IV.
.
Результаты
записываем в разделе IV.
Обратный ход:
В разделе V записываем единицы, как это указано в табл. 1, вычисляем x4=a
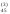 /a
/a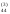 .
.Для вычисления значений x3,x2,x1 используются лишь строки разделов I, II, III, содержащие единицы (отмеченные строки). Так для вычисления x3 умножаем x4 на b
 и получившееся произведение вычитаем
из b
и получившееся произведение вычитаем
из b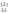 .
При этом единицы, расставленные в
разделе V,
помогают находить для xi
(i=3,2,1)
соответствующие коэффициенты в
отмеченных строках. Таким образом,
.
При этом единицы, расставленные в
разделе V,
помогают находить для xi
(i=3,2,1)
соответствующие коэффициенты в
отмеченных строках. Таким образом,
x3=
b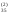 -
b
-
b x4.
x4.
Вычисляем x2, и затем x1, для чего используем элементы отмеченной строки раздела II: x2= b
 -
b
-
b x4-
b
x4-
b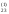 x3,
x3,
x1=
b -
b
-
b x4
- b
x4
- b x3
- b
x3
- b x2.
x2.
Компактная схема Гаусса оказывается особенно выгодной при одновременном решении нескольких систем, отличающихся лишь столбцами свободных членов, при вычислении обратной матрицы.
Решим с помощью компактной схемы Гаусса
систему уравнений, все вычисления
занесем в таблицу
(табл.2):

Следуя порядку действий, указанному в параграфе 1, получаем значения неизвестных: x4=0,068976; х3=-1,815417; x2=0,964032; х1=4,870672.
Проверка показывает, с какой точностью получен результат, погрешность вычислений не превосходит соответственно 0,0000029; 0,0000028; 0,000001; 0,000016 в первом, втором, третьем и четвертом уравнениях.
Таблица 2
|
|
i |
x1 |
x2 |
x3 |
x4 |
Свободные члены |
|
|
|
I |
1 |
2 |
-3,5 |
2,7 |
-8,2 |
0,9 |
-6,1 |
|
|
2 |
1 |
2,8 |
3,6 |
2,4 |
1,2 |
11 |
| |
|
3 |
1 |
2,5 |
-3,8 |
-2,6 |
14 |
11,1 |
| |
|
4 |
5 |
-6 |
4,8 |
2,1 |
10 |
15,9 |
| |
|
|
1 |
-1,75 |
1,35 |
-4,1 |
0,45 |
-3,05 |
-3,05 | |
|
II |
2 |
|
4,55 |
2,25 |
6,5 |
0,75 |
14,05 |
14,05 |
|
3 |
|
4,25 |
-5,15 |
1,5 |
13,55 |
14,15 |
14,15 | |
|
4 |
|
2,75 |
-1,95 |
22,6 |
7,75 |
31,15 |
31,15 | |
|
|
|
1 |
0,494505 |
1,428571 |
0,164835 |
3,087912 |
3,087912 | |
|
III |
3 |
|
|
-7,251648 |
-4,571429 |
12,849451 |
1,026374 |
1,026374 |
|
4 |
|
|
-3,30989 |
18,671429 |
7,296703 |
22,658242 |
22,658242 | |
|
|
|
|
1 |
0,630399 |
-1,771935 |
-0,141537 |
-0,141537 | |
|
IV |
4 |
|
|
|
20,757978 |
1,431793 |
22,189771 |
22,189771 |
|
|
|
|
|
1 |
0,068976 |
1,068976 |
1,068976 | |
|
V |
|
|
|
|
1 |
0,068976 |
|
0,0000029 |
|
|
|
|
1 |
|
-1,815417 |
|
0,0000028 | |
|
|
|
1 |
|
|
0,964032 |
|
0,000001 | |
|
|
1 |
|
|
|
4,870672 |
|
0,000016 |
