
- •Глава II. Элементы векторной алгебры и аналитической геометрии
- •§1. Система координат
- •1.1 Система координат на плоскости (пространство r2 )
- •1.2 Простейшие задачи аналитической геометрии Расстояние между двумя точками на плоскости
- •Деление отрезка в данном отношении
- •§2 Векторы.
- •1.Основные понятия
- •2. Линейные операции с векторами Сложение векторов
- •Вычитание
- •Умножение вектора на число
- •3. Проекция вектора на ось
- •4.Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы
- •Обозначим проекции на координатные оси, через.
- •5. Действия над векторами в координатной форме
- •§3. N- мерное векторное пространство. Линейная зависимость и независимость векторов.
- •§4. Скалярное, векторное и смешанное произведения векторов
- •4.1 Скалярное произведение, его свойства и вычисление
- •Механический смысл скалярного произведения
- •Геометрический смысл векторного произведения
- •Механический смысл векторного произведения
- •Свойства векторного произведения
- •Векторное произведение векторов, заданных координатами
- •4.3 Смешанное (векторно-скалярное) произведение векторов, его геометрический смысл
- •Свойства смешанного произведения
- •Смешанное произведение векторов, заданных координатами
Свойства векторного произведения
10 Векторное произведение равно нулю, если векторы коллинеарны или один из них равен нулю.
![]() следует
из определения модуля векторного
произведения:
следует
из определения модуля векторного
произведения:
![]() .
.
Модуль равен нулю, если:
1)
![]() или
или![]() векторы
векторы![]() коллинеарны.
коллинеарны.
2)
![]() или
или![]() .
.
20
![]() ,
т.е. векторное произведение не коммутативно.
,
т.е. векторное произведение не коммутативно.
30![]() (сочетательный закон относительно
числового множителя).
(сочетательный закон относительно
числового множителя).
40.![]() (распределительный закон относительно
суммы и произведения).
(распределительный закон относительно
суммы и произведения).
Векторное произведение векторов, заданных координатами
Пусть
заданы векторы
![]() и
и![]() .
.
Векторное
произведение векторов, заданных
координатами, равно определителю
третьего порядка, первой строкой которого
являются единичные векторы
![]() и
и![]() ,
второй- координаты первого перемножаемого
вектора, третьей – координаты второго
вектора:
,
второй- координаты первого перемножаемого
вектора, третьей – координаты второго
вектора:
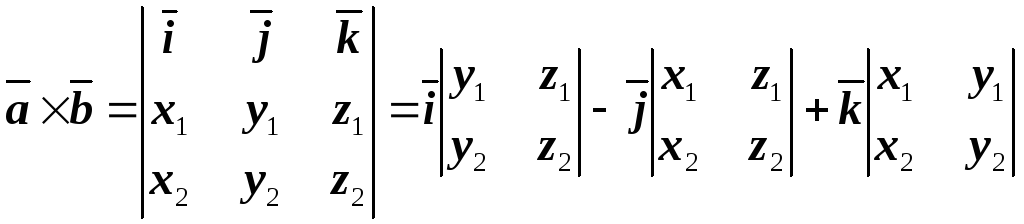 .
(4.10)
.
(4.10)
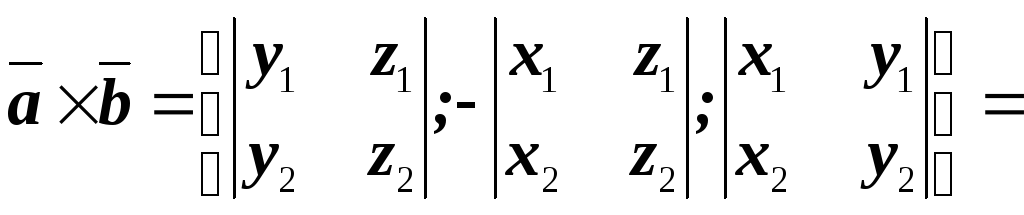
![]() .
(4.11)
.
(4.11)
Практический способ вычисления векторного произведения
Записать векторы один под другим
![]()
![]()
и, вычёркивая последовательно столбцы одноимённых координат, получаем определители второго порядка, которые являются координатами векторного произведения. При вычислении второй координаты перед определителем изменить знак.
Составить выражение из координат:
![]() .
(4.12)
.
(4.12)
Для получения координат векторного произведения в выражении (4.12) поочередно вычеркивать столбцы.
Для получения первой координаты x вычеркнуть 1-й столбец:
![]()
Для получения y вычеркнуть второй столбец, перед оставшимся минором взять знак « - »:
![]() .
.
Для z вычеркнуть 3-й столбец:
![]()
4.3 Смешанное (векторно-скалярное) произведение векторов, его геометрический смысл
Опр 4 Смешанным произведением векторов называется число, полученное в результате векторного произведения двух векторов, скалярно умноженного на третий.
Обозначается
![]() .(4.13)
.(4.13)
Геометрический смысл его выражается теоремой.
Теорема.
Смешанное произведение представляет
собой число, абсолютная величина которого
равна объёму параллелепипеда, построенного
на векторах
![]() как на составляющих, т.е.
как на составляющих, т.е.
![]() .
(4.14)
.
(4.14)
Подставляя эти значения в формулу (*), получим, что и требовалось доказать.
Свойства смешанного произведения
10
Смешанное произведение равно нулю, если
векторы
![]() -
компланарны, один из них нулевой или
какие-либо два из них коллинеарные.
-
компланарны, один из них нулевой или
какие-либо два из них коллинеарные.
20 Можно ли переставлять местами сомножители в смешанном произведении?
Там, где произведение скалярное, там можно, а где векторное– нельзя.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;![]() .
.
Если расположить векторы по координатным осям, то, делая круговой поворот их против часовой стрелки (рисунок 20), смешанное произведение не меняет знак.
![]() .
.
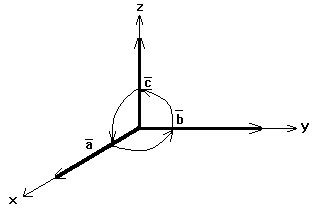 Рис.
20
Рис.
20
Если вращать векторы по ходу часовой стрелки, то смешанное произведение меняет знак на противоположный (рисунок 21).
![]() .
.
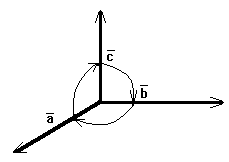 Рис.
21
Рис.
21
Смешанное произведение векторов, заданных координатами
Пусть
векторы
![]() заданы координатами
заданы координатами
![]() ,
,
![]() ,
,![]() .
.
Тогда смешанное произведение их вычисляется с помощью определителя третьего порядка, строками которого являются координаты перемножаемых векторов.
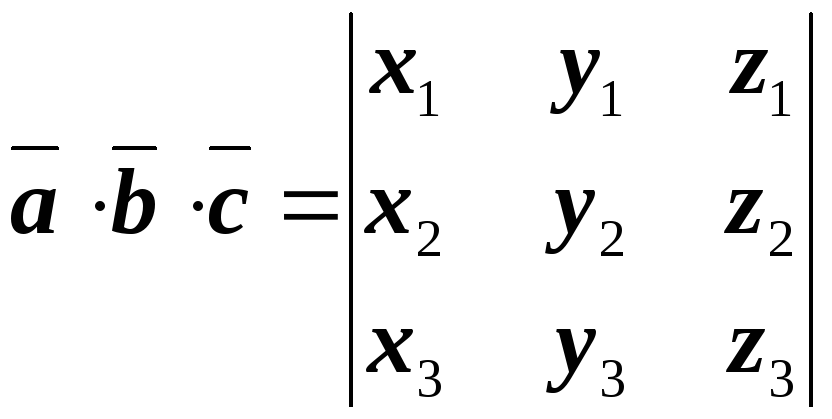 .
(4.15)
.
(4.15)
