2.3. Нелинейная регрессия

Рассмотрим случай, когда зависимость нелинейна по переменным х, например модель вида

(2.6)

На рис. 2.1 изображено поле корреляции. Очевидно, что зависимость между Y и X нелинейная и её графическим изображением является не прямая, а кривая. Оценкой выражения (2.6) является уравнение регрессии

где и— оценки коэффициентов регрессиии.

Принцип нахождения коэффициентов тот же — метод наименьших квадратов, т.е.

или

Дифференцируя последнее равенство по ии приравнивая правые части нулю, получаем так называемую систему нормальных уравнений:

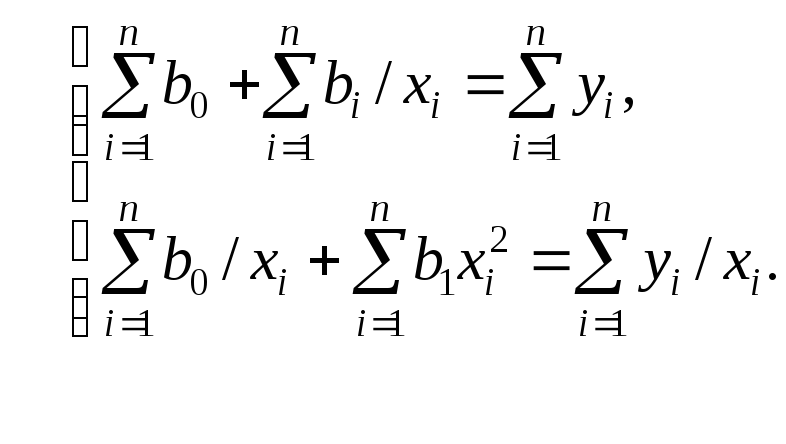_(2.7)

В общем случае нелинейной зависимости между переменными Y и X связь может выражаться многочленом k-й степени от х:

Коэффициенты регрессии определяют по принципу наименьших квадратов. Система нормальных уравнений имеет вид

Вычислив коэффициенты системы, её можно решить любым известным способом.

2.4. Оценка значимости коэффициентов регрессии. Интервальная оценка коэффициентов регрессии

Проверить значимость оценок коэффициентов регрессии — значит установить, достаточна ли величина оценки для статистически обоснованного вывода о том, что коэффициент регрессии отличен от нуля. Для этого проверяют гипотезу о равенстве нулю коэффициента регрессии, соблюдая предпосылки «нормальной регрессии». В этом случае вычисляемая для проверки нулевой гипотезы Н₀: β=0 статистика

(2.8)

имеет распределение Стьюдента с k=n-2 степенями свободы (b — оценка коэффициента регрессии, — оценка среднеквадратического отклонения коэффициента регрессии, иначе стандартная ошибка оценки). По уровню значимостиα и числу степеней свободы k находят по таблицам распределения Стьюдента (см. табл. 1 приложений) критическое значение , удовлетворяющее условию. Если, то нулевую гипотезу о равенстве нулю коэффициента регрессии отвергают, коэффициент считают значимым. Принет оснований отвергать нулевую гипотезу.

Оценки среднеквадратического отклонения коэффициентов регрессии вычисляют по следующим формулам:

(2.9)

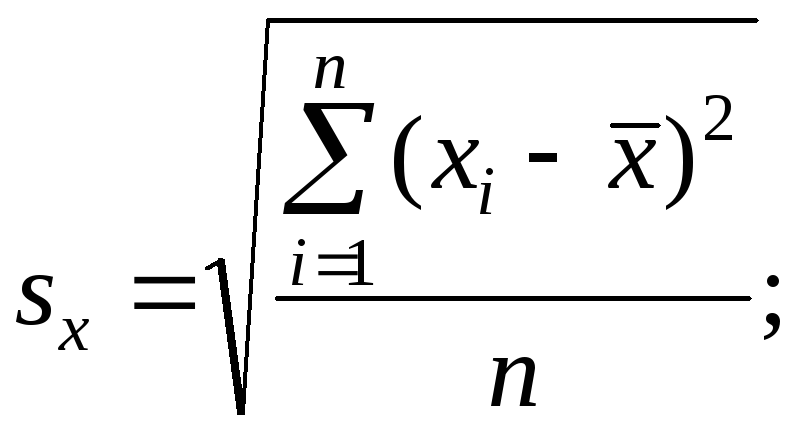
где — оценка остаточной дисперсии, вычисляемая по формуле (2.5).

Доверительный интервал для значимых параметров строят по обычной схеме. Из условия

где α — уровень значимости, находим

(2.10)

2.5. Интервальная оценка для условного математического ожидания

Линия регрессии характеризует изменение условного математического ожидания результативного признака от вариации остальных признаков. Точечной оценкой условного математического ожидания M(Y\X=x) является условное среднее . Кроме точечной оценки дляM(Y\X=x) можно построить доверительный интервал в точке х=х₀.

Известно, что имеет распределение Стьюдента сk=n—2 степенями свободы. Найдя оценку среднеквадратического отклонения для условного среднего, можно построить доверительный интервал для условного математического ожидания M(Y\X=x) в точке х=х₀.

Оценку дисперсии условного среднего вычисляют по формуле

или для интервального ряда

(2.11)

Доверительный интервал находят из условия

где α — уровень значимости. Отсюда

Доверительный интервал для условного математического ожидания можно изобразить графически (рис, 2.2).

Из рис. 2.2 видно, что в точке границы интервала наиболее близки друг другу. Расположение границ доверительного интервала показывает, что прогнозы по уравнению регрессии, хороши только в случае, если значениех не выходит за пределы выборки, по которой вычислено уравнение регрессии; иными словами, экстраполяция по уравнению регрессии может привести к значительным погрешностям.