1.6. Проверка гипотезы о значимости коэффициента корреляции

На практике коэффициент корреляции ρ обычно неизвестен. По результатам выборки может быть найдена его точечная оценка — выборочный коэффициент корреляции r.

Равенство нулю выборочного коэффициента корреляции ещё не свидетельствует о равенстве нулю самого коэффициента корреляции, а следовательно, о некоррелированности случайных величин X и Y. Чтобы выяснить, находятся ли случайные величины в корреляционной зависимости, нужно проверить значимость выборочного коэффициента корреляции r, т.е. установить, достаточна ли его величина для обоснованного вывода о наличии корреляционной связи. Для этого проверяют нулевую гипотезу . Предполагается наличие двумерного нормального распределения случайных переменных; объём выборки может быть любым. Вычисляют статистикукоторая имеет распределение Стьюдента сk=n-2 степенями свободы. Для проверки нулевой гипотезы по уровню значимости α и числу степеней свободы k находят по таблицам распределения Стьюдента (t-распределение; см. табл. 1 приложения) критическое значение , удовлетворяющее условию. Если, то нулевую гипотезу об отсутствии корреляционной связи между переменнымиX и Y следует отвергнуть. Переменные считают зависимыми. При нет оснований отвергать нулевую гипотезу.

В случае значимого выборочного коэффициента, корреляции есть смысл построить доверительный интервал для коэффициента корреляций ρ. Однако для этого нужно знать закон распределения выборочного коэффициента корреляции r.

Плотность вероятности выборочного коэффициента корреляции имеет сложный вид, поэтому прибегают к специально подобранным функциям от выборочного коэффициента корреляции, которые сводятся к хорошо изученным распределениям, например нормальному или Стьюдента. Чаще всего для подбора функции применяют преобразование Фишера. Вычисляют статистику:

где r=thz — гиперболический тангенс от z.

Распределение статистики z хорошо аппроксимируется нормальным распределением с параметрами

В этом, случае доверительный интервал для ρимеетвид. Величиныинаходят по таблицам по следующим значениям:

где — нормированная функция Лапласа дляq % доверительного интервала (см. табл. 2 приложений значение функции ).

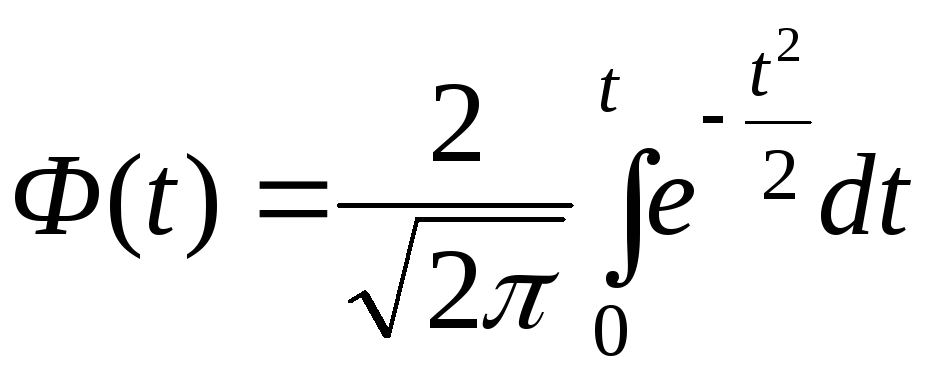Если коэффициент корреляции значим, то коэффициенты регрессии также значимо отличаются от нуля, а интервальные оценки для них можно получить по следующим формулам:

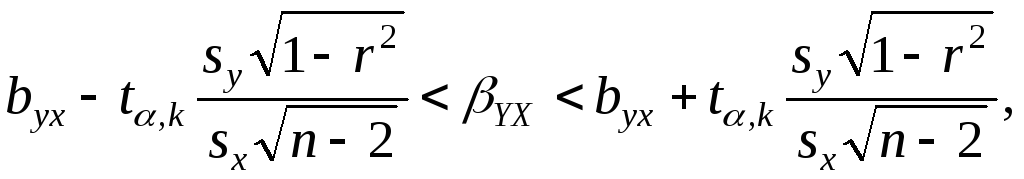(1.7)

(1.8)

где имеет распределение Стьюдента сk=n—2 степенями свободы.

1.7. Корреляционное отношение

На практике часто предпосылки корреляционного анализа нарушаются: один из признаков оказывается величиной не случайной, или признаки не имеют совместного нормального распределения. Однако статистическая зависимость между ними существует. Для изучения связи между признаками в этом случае существует общий показатель зависимости признаков, основанный на показателе изменчивости — общей (или полной) дисперсии.

Полной называется дисперсия признака относительно его математического ожидания. Так, для признака Y это . Дисперсиюможно разложить на две составляющие, одна из которых характеризует влияние фактораX на Y, другая — влияние прочих факторов. Очевидно, чем меньше влияние прочих факторов, тем теснее связь, тем более приближается она к функциональной. Представим в следующем виде:

. (1.9)

Первое слагаемое обозначим . Это дисперсия функции регрессии относительно математического ожидания признака (в данном случае признакаY);.она измеряет влияние признака X на Y. Второе слагаемое обозначим . Это дисперсия признакаY относительно функции регрессии. Её называют также средней из условных дисперсий или остаточной дисперсиейизмеряет влияние наY прочих факторов.

Покажем, что действительно можно разложить на два таких слагаемых:

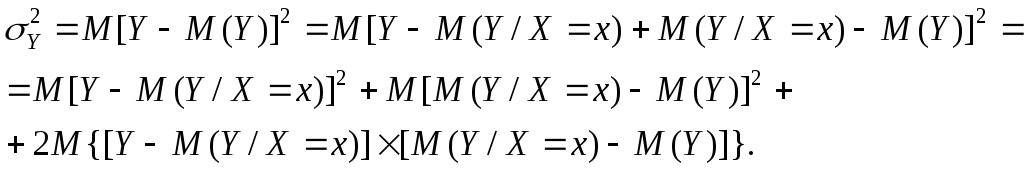(1.10)

Для простоты полагаем распределение дискретным. Имеем

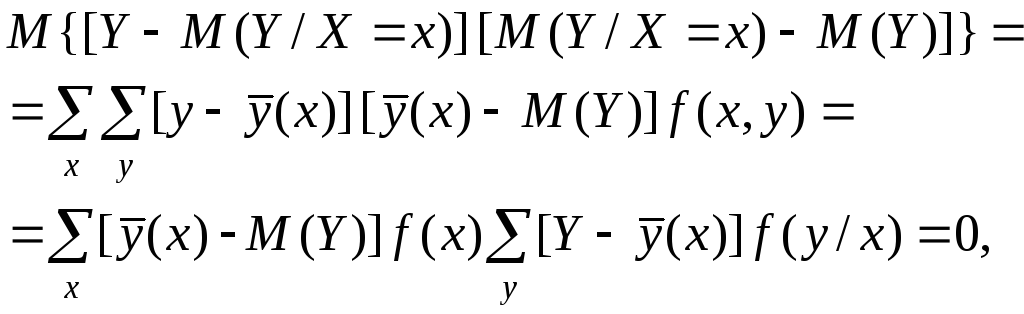
так как при любом х справедливо равенство

Третье слагаемое в равенстве (1.10) равно нулю, поэтому равенство (1.9) справедливо. Поскольку второе слагаемое в равенстве (1.9) оценивает влияние признака X на Y, то его можно использовать для оценки тесноты связи между X и Y. Тесноту связи удобно оценивать в единицах общей дисперсии , т.е. рассматривать отношение. Эту величину обозначаюти называют теоретическим корреляционным отношением. Таким образом,

(1.11)

Разделив обе части равенства (1.9) на получим

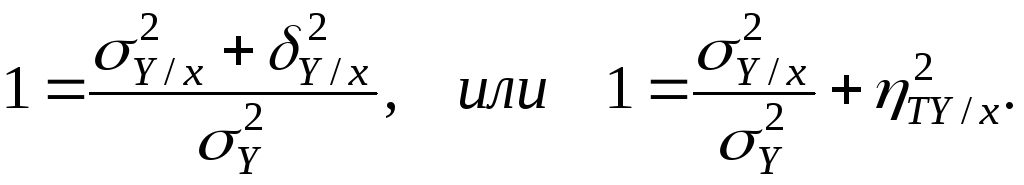
Из последней формулы имеем

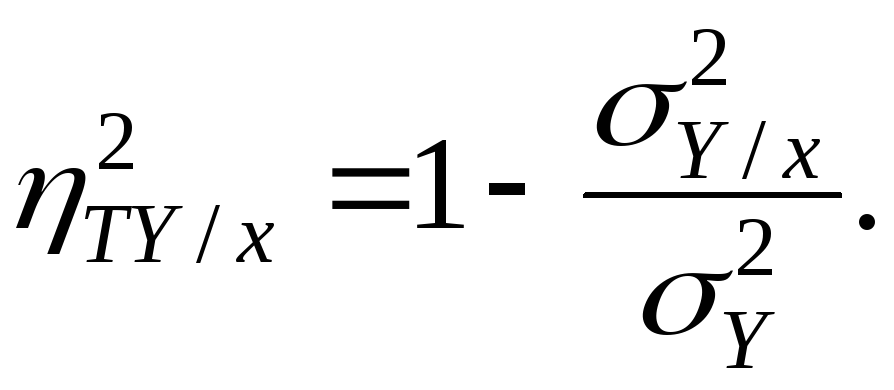_(1.12)

Поскольку , так как— составная часть, то из равенства (1.12) следует, что значениевсегда заключено между нулем и единицей.

Все сделанные выводы справедливы и для . Из равенства (1.12) следует, чтотолько тогда, когда, т.е. отсутствует влияние прочих факторов и всё распределение сконцентрировано на кривой регрессии. В этом случае междуY и X существует функциональная зависимость. Далее, из равенства (1.12) следует, что тогда и только тогда, когда

=M(Y) = const, т.е. линия регрессии Y по X — горизонтальная прямая, проходящая через центр распределения. В этом случае можно сказать, что переменная Y не коррелирована с X (рис. 1.2,а, б, в).

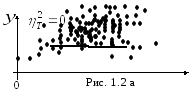
Аналогичными свойствами обладает— показатель тесноты связи

между X и Y.

Часто используют величину

. (1.13)

Считают, что она не может быть отрицательной. Значения величины (или) также могут находиться лишь в пределах от нуля до единицы. Это очевидно из формулы (1.13).

Значения , лежащие в интервале 0<<1, являются показателями тесноты группировки точек около кривой регрессии независимо oт её вида (формы связи). Корреляционное отношениесвязано сследующим образом:. В случае линейной зависимости между переменными. Разностьможет быть использована как показатель нелинейности связи между переменными.

При вычислении по выборочным данным получаем выборочное корреляционное отношение. Обозначим его. Вместо дисперсий в этом случае используются их оценки. Тогда формула (1.12) принимает вид