1.4. Свойства коэффициента корреляции

Коэффициент корреляции является одним из самых распространенных способов измерения связи между случайными переменными. Рассмотрим некоторые свойства этого коэффициента.

Теорема 1. Коэффициент корреляции принимает значения на интервале (-1, +1).

Доказательство. Докажем справедливость утверждения для случая дискретных переменных. Запишем явно неотрицательное выражение:

Возведём выражение под знаком суммы в квадрат:

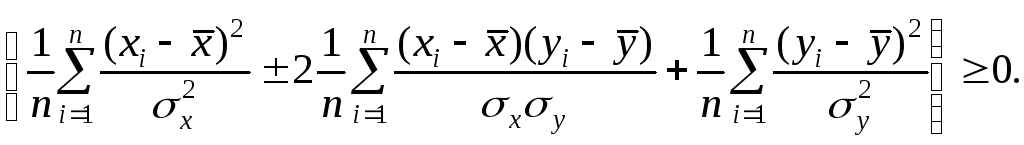
Первое и третье из слагаемых равны единице, поскольку из определения дисперсии следует, что —и. Таким образом, окончательно получаем 1±2ρ+1≥0, откуда -l≤ρ≤+1.

Если коэффициент корреляции положителен, то связь между переменными также положительна и значения переменных увеличиваются или уменьшаются одновременно. Если коэффициент корреляции имеет отрицательное значение, то при увеличении одной переменной уменьшается другая.

Приведём следующее важное свойство коэффициента корреляции: коэффициент корреляции не зависит от выбора начала отсчёта и единицы измерения, т. е. от любых постоянных и,итаких, что>0 и>0, т.е.

.

Таким образом, переменные X и Y можно уменьшать или увеличивать в а раз, а также вычитать или прибавлять к значениям X и Y одно и то же число b. В результате величина коэффициента корреляции не изменится.

Если коэффициент корреляции , то случайные переменные некоррелированы. Понятие некоррелированности не следует смешивать с понятием независимости, независимые величины всегда некоррелированы. Однако обратное утверждение невероятно: некоррелированные величины могут быть зависимы и даже функционально, однако эта связь не линейная.

Выборочный коэффициент корреляции вычисляют по формуле (1.2). Имеется несколько модификаций этой формулы, которые удобно использовать при той или иной форме представления исходной информации. Так, при малом числе наблюдений выборочный коэффициент корреляции удобно вычислять по формуле

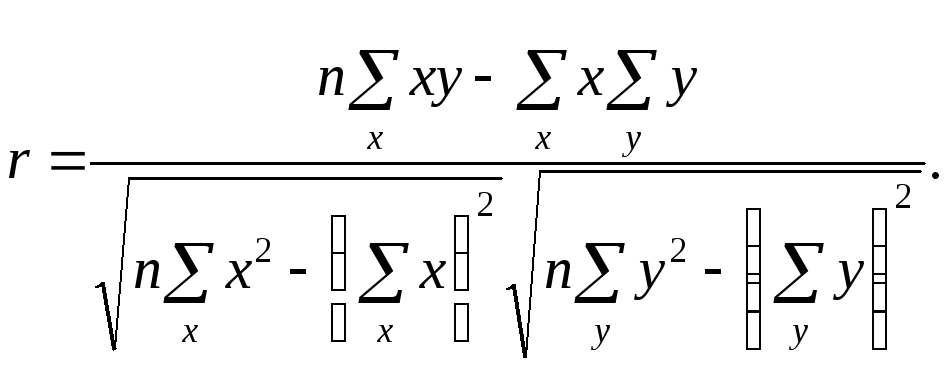
Если информация имеет вид корреляционной таблицы (см. п 1.5), то удобно пользоваться формулой

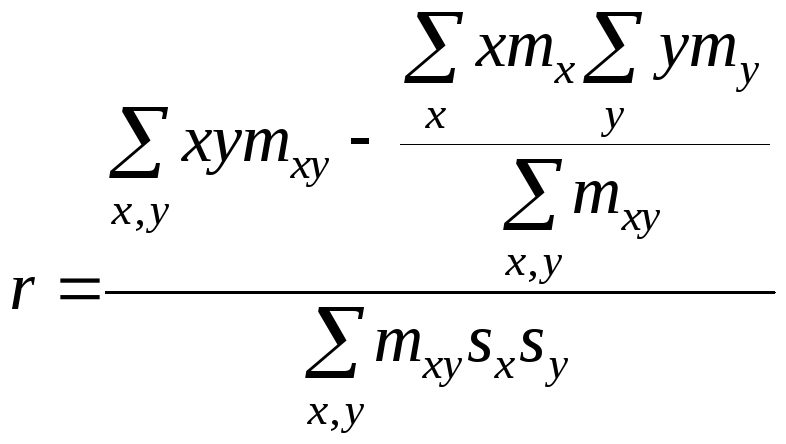, (1.5)

где — суммарная частота наблюдаемого значения признаках при всех значениях у;— суммарная частота наблюдаемого значения признакаупри всех значениях х; — частота появления пары признаков (х, у).

Из формулы (1.2) очевидно, что , т.е. величина выборочного коэффициента корреляции не зависит от порядка следования переменных, поэтому обычно пишут простоr.

1.5. Поле корреляции. Вычисление оценок параметров двумерной модели

На практике для вычисления оценок параметров двумерной модели удобно использовать корреляционную таблицу и поле корреляции. Пусть, например, изучается зависимость между объёмом выполненных работ (у) и накладными расходами (х). Имеем выборку из генеральной совокупности, состоящую из 150 пар переменных (). Считаем, что предпосылки корреляционного анализа выполнены.

Пару случайных чисел () можно изобразить графически в виде точки с координатами (). Аналогично можно изобразить весь набор пар случайных чисел (всю выборку). Однако при большом объёме выборки это затруднительно. Задача упрощается, если выборку упорядочить, т.е. переменные сгруппировать. Сгруппированные ряды могут быть как дискретными, так и интервальными.

По осям координат откладывают или дискретные значения переменных, или интервалы их изменения. Для интервального ряда наносят координатную сетку. Каждую пару переменных из данной выборки изображают в виде точки с соответствующими координатами для дискретного ряда или в виде точки в соответствующей клетке для интервального ряда. Такое изображение корреляционной зависимости называют полем корреляции. На рис. 1.1 изображено поле корреляции для выборки, состоящей из 150 пар переменных (ряд интервальный).

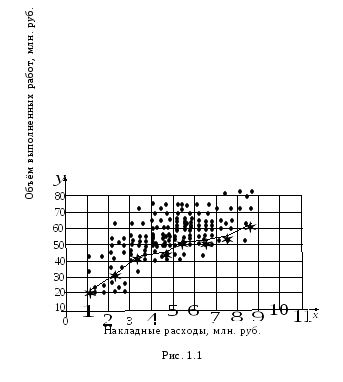
Если вычислить средние значения у в каждом интервале изменения х [обозначим их )], нанести эти точки на рис. 1.1 и соединить между собой, то получим ломаную линию, по виду которой можно судить, как в среднем меняютсяу в зависимости от изменения х. По виду этой линии можно также сделать предположение о форме связи между переменными. В данном случае ломаную линию можно аппроксимировать прямой линией, так как она достаточно хорошо приближается к ней. По выборочным данным можно построить также корреляционную табл. 1.1.

Таблица 1.1

Накладные расходы, млн. руб.	1÷2 1,5	2÷3 2,5	3÷4 3,5	4÷5 4,5	5÷6 5,5	6÷7 6,5	7÷8 7,5	8÷9 8,5
Объём выполненных работ, млн. руб.
10÷20 15	4	5							9
20÷30 25	1	3	1						5
30÷40 35	2	3	6	5	3	1			20
40÷50 45		5	9	19	8	7	2	1	51
50÷60 55		1	2	7	16	9	4	2	41
60÷70 65			1	5	6	4	2	2	20
70÷80 75							1	3	4
	7	17	19	36	33	21	9	8	150

Корреляционную таблицу, как и поле корреляции, строят по сгруппированному ряду (дискретному или интервальному). Табл. 1.1 построена на основе интервального ряда. В первой строке и первом столбце таблицы помещают интервалы изменения х и у и значения середин интервалов. Так, например, 1,5 — середина интервала изменения х=l÷2,15— середина интервала изменения у=10÷20. В ячейки, образованные пересечением строк и столбцов, заносят частоты попадания пар значений (х, у) в соответствующие интервалы по х и у. Например, частота 4 означает, что в интервал изменения у от 10 до 20 попало 4 пары наблюдавшихся значений. Эти частоты обозначают . В 9-й строке и 10-м столбце находятся значенияи- суммыпо соответствующим столбцу и строке.

Как будет показано в дальнейшем, корреляционно таблицей удобно пользоваться при вычислении коэффициентов корреляций и параметров уравнений регрессии.

Корреляционная таблица построена на основе интервального ряда, поэтому для оценок параметров воспользуемся формулами гл. 1 для вычисления средней арифметической и дисперсии. Имеем:

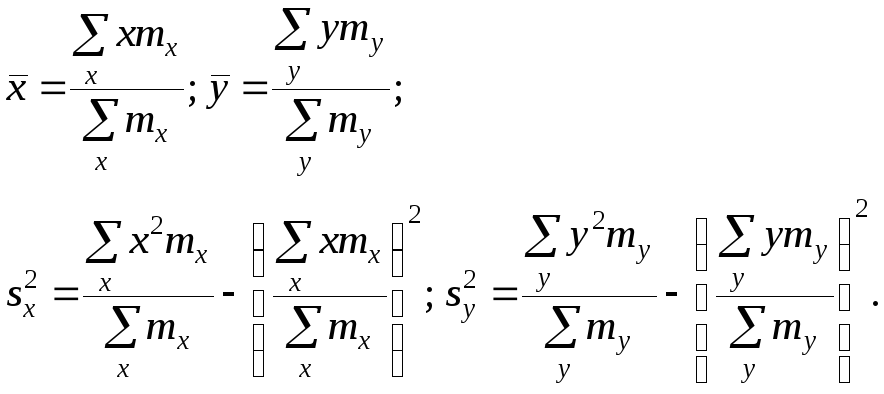(1.6)