2. Регрессионный анализ

2.1. Основные положения регрессионного анализа

Основная задача регрессионного анализа — изучение зависимости между результативным признаком Y и наблюдавшимся признаком Х, оценка функции регрессий.

Предпосылки регрессионного анализа:

1) Y — независимые случайные величины, имеющие постоянную дисперсию;

2) X — величины наблюдаемого признака (величины не случайные);

3) условное математическое ожидание М(Y |Х=х) можно представить в виде

_(2.1)

Выражение (2.1), как уже упоминалось в п. 1.2, называется функцией регрессии (или модельным уравнением регрессии) Y на X. Оценке в этом выражении подлежат параметры и, называемые коэффициентами регрессии, а также— остаточная дисперсия.

Остаточной дисперсией называется та часть рассеивания результативного признака, которую нельзя объяснить действием наблюдаемого признака; Остаточная дисперсия может служить для оценки точности подбора вида функции регрессии (модельного уравнения регрессии), полноты набора признаков, включенных в анализ. Оценки параметров функции регрессии находят, используя метод наименьших квадратов.

В данном вопросе рассмотрен линейный регрессионный анализ. Линейным он называется потому, что изучаем лишь те виды зависимостей , которые линейны по оцениваемым параметрам, хотя могут быть нелинейны по переменнымX. Например, зависимости линейны относительно параметров,, хотя вторая и третья зависимости нелинейны относительно переменныхх. Вид зависимости выбирают, исходя из визуальной оценки характера расположения точек на поле корреляции; опыта предыдущих исследований; соображений профессионального характера, основанных и знании физической сущности процесса.

Важное место в линейном регрессионном анализе занимает так называемая «нормальная регрессия». Она имеет место, если сделать предположения относительно закона распределения случайной величины Y. Предпосылки «нормальной регрессии»:

1) Y — независимые случайные величины, имеющие постоянную дисперсию и распределенные по нормальному закону;

2) X — величины наблюдаемого признака (величины не случайные);

3) условное математическое ожидание M(Y\X=x) можно представить в виде (2.1).

В этом случае оценки коэффициентов регрессии — несмещённые с минимальной дисперсией и нормальным законом распределения. Из этого положения следует что при «нормальной регрессии» имеется возможность оценить значимость оценок коэффициентов регрессии, а также построить доверительный интервал для коэффициентов регрессии и условного математического ожидания M(Y\X=x).

2.2. Линейная регрессия

Рассмотрим простейший случай регрессионного анализа — модель вида (2.1), когда зависимость линейна и по оцениваемым параметрам, и по переменным. Оценки параметров модели (2.1) и обозначил и. Оценку остаточной дисперсииобозначим. Подставив в формулу (2.1) вместо параметров их оценки, получим уравнение регрессии, коэффициенты которогоинаходят из условия минимума суммы квадратов отклонений измеренных значений результативного признакаот вычисленных по уравнению регрессии

или

Составим систему нормальных уравнений: первое уравнение

_откуда

второе уравнение

_откуда

_Итак,

_(2.2)

Оценки, полученные по способу наименьших квадратов, обладают минимальной дисперсией в классе линейных оценок. Решая систему (2.2) относительно инайдём оценки параметрови:

_(2.3)

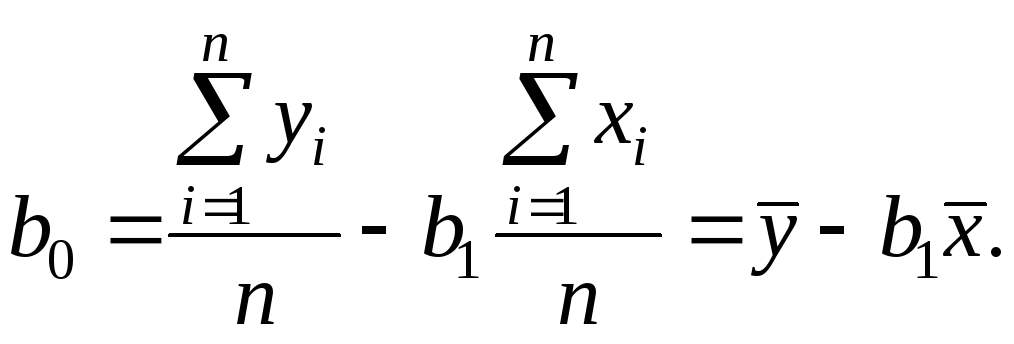_(2.4)

Остаётся получить оценку параметра . Имеем

_(2.5)

где п — количество наблюдений.

Если п велико, то для упрощения расчётов наблюдавшиеся данные принята группировать, т.е. строить корреляционную таблицу. Пример построения такой таблицы приведен в п. 1.5. Формулы для нахождения коэффициентов регрессии по сгруппированным данным те же, что и для расчёта по несгруппированным данным, но суммы заменяют на

где — частоты повторений соответствующих значений переменных. В дальнейшем часто используется этот наглядный приём вычислений.