2.6. Проверка значимости уравнения регрессии

Оценить значимость уравнения регрессии — значит установить, соответствует ли математическая, модель, выражающая зависимость между Y и Х, экспериментальным данным. Для оценки значимости в предпосылках «нормальной регрессии» проверяют гипотезу Н₀: =0. Если она отвергается, то считают, что междуY и X нет связи (или связь нелинейная). Для проверки нулевой гипотезы используют основное положение дисперсионного анализа о разбиении суммы квадратов на слагаемые. Воспользуемся разложением . Общая сумма квадратов отклонений результативного признакаразлагается наQ₁ (сумму, характеризующую влияние признака X) и Q₂ (остаточную сумму квадратов, характеризующую влияние неучтённых факторов). Очевидно, чем меньше влияние неучтённых факторов, тем лучше математическая модель соответствует экспериментальным данным, так как вариация Y в основном объясняется влиянием признака X.

Для проверки нулевой гипотезы вычисляют статистику которая имеет распределение Фишера-Снедекора с=l,=n-2 степенями свободы (вп - число наблюдений). По уровню значимости α и числу степеней свободы инаходят по таблицамF-распределение для уровня значимости α=0,05 (см. табл. 3 приложений) критическое значение , удовлетворяющее условию. Если, нулевую гипотезу отвергают, уравнение считают значимым. Еслито нет оснований отвергать нулевую гипотезу.

2.7. Многомерный регрессионный анализ

В случае, если изменения результативного признака определяются действием совокупности других признаков, имеет место многомерный регрессионный анализ. Пусть результативный признак Y, а независимые признаки Для многомерного случая предпосылки регрессионного анализа можно сформулировать следующим образом:Y - независимые случайные величины со средним и постоянной дисперсией— линейно независимые векторыВсе положения, изложенные в п.2.1, справедливы для многомерного случая. Рассмотрим модель вида

_(2.13)

Оценке подлежат параметры и остаточная дисперсия. Заменив параметры их оценками, запишем уравнение регрессии

_(2.14)

Коэффициенты в этом выражении находят методом наименьших квадратов.

Исходными данными для вычисления коэффициентов является выборка из многомерной совокупности, представляемая обычно в виде матрицыX и вектора Y:

АВТОНОМНАЯ НЕКОММЕРЧЕСКАЯ ОРГАНИЗАЦИЯ 1

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ 1

ЦЕНТРОСОЮЗА РОССИЙСКОЙ ФЕДЕРАЦИИ 1

КАЗАНСКИЙ КООПЕРАТИВНЫЙ ИНСТИТУТ (ФИЛИАЛ) 1

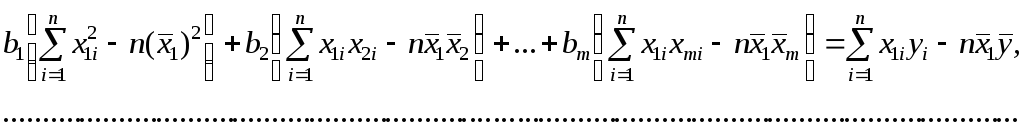
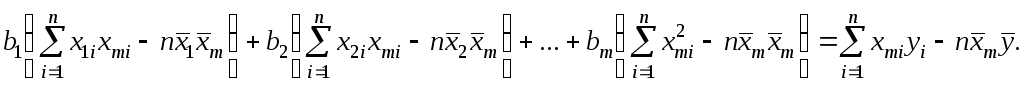Пусть С — матрица коэффициентов при неизвестных параметрах ;— матрица, обратная матрицеС; — элемент, стоящий на пересечении i-й строки и i-го столбца матрицы — выражение. Тогда, используя формулы линейной алгебры, запишем окончательные выражения для параметров:

(2.17)

Оценкой остаточной дисперсии является

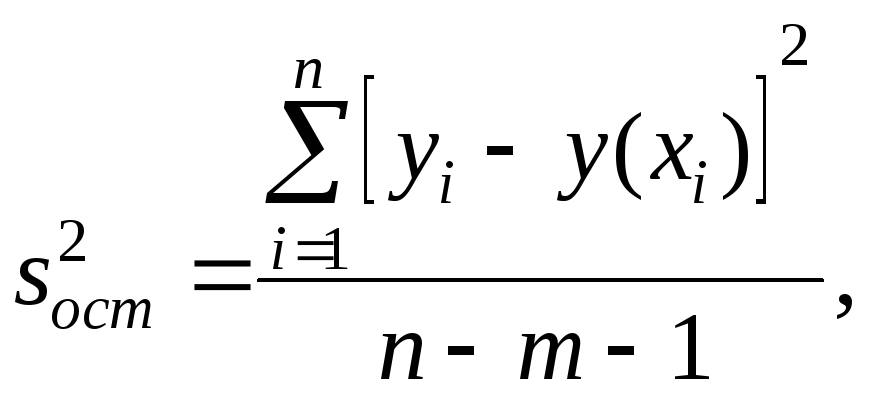
где — измеренное значение результативного признака;значение результативного признака, вычисленное по уравнению регрессий.

Если выборка получена из нормально распределенной генеральной совокупности, то, аналогично изложенному в п. 2.4, можно проверить значимость оценок коэффициентов регрессии, только в данном случае статистику вычисляют для каждогоj-го коэффициента регрессии (2.18)

где —элемент обратной матрицы, стоящий на пересеченииi-й строки и j-го столбца; — диагональный элемент обратной матрицы.

При заданном уровне значимости α и числе степеней свободы k=n—т—1 по табл. 1 приложений находят критическое значение . Если, то нулевую гипотезу о равенстве нулю коэффициента регрессии отвергают. Оценку коэффициента считают значимой. Такую проверку производят последовательно для каждого коэффициента регрессии. Если, то нет оснований отвергать нулевую гипотезу, оценку коэффициента регрессии считают незначимой.

Для значимых коэффициентов регрессии целесообразно построить доверительные интервалы по формуле (2.10). Для оценки значимости уравнения регрессии следует проверить нулевую гипотезу о том, что все коэффициенты регрессии (кроме свободного члена) равны нулю: ( — вектор коэффициентов регрессии). Нулевую гипотезу проверяют, так же как и в п. 2.6, с помощью статистики , гдеQ₁ — сумма квадратов, характеризующая влияние признаков Х; Q_ocт — остаточная сумма квадратов, характеризующая влияние неучтённых факторов; k₂=n—m—1, k₁=m. Для уровня значимости α и числа степеней свободы k₁ и k₂ по табл. 3 приложений находят критическое значение . Если, то нулевую гипотезу об одновременном равенстве нулю коэффициентов регрессии отвергают. Уравнение регрессии считают значимым. Принет оснований отвергать нулевую гипотезу, уравнение регрессии считают незначимым.