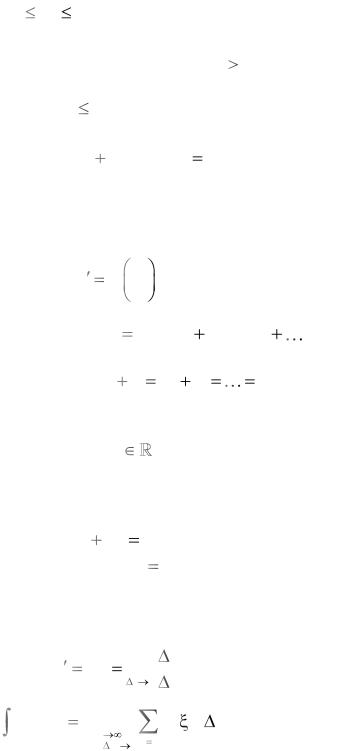
№

Термин

Значение

п/п

89.

Ограниченная после-

Последовательность {yn } называется ограни-

довательность

ченной с обеих сторон (или просто ограни-

ченной), если она ограничена и сверху, и сни-

зу, т.е. если существуют два вещественных

числа M и m такие,

что каждый элемент этой

последовательности

yn

удовлетворяет нера-

венствам m

yn

M .

90.

Ограниченная функ-

Функция y=f (x) называется ограниченной на

ция

интервале, если существует число C

0 такое,

что для всех x из этого интервала выполняется

C .

неравенство

f (x)

91.

Однородное диффе-

Дифференциальное уравнение вида

ренциальное уравне-

Pn (x, y)dx Qn (x, y)dy 0 ,

ние первого порядка

где Pn (x, y)

и Qn (x, y)

– однородные много-

в дифференциальной

члены одинаковой степени n.

форме

92.

Однородное диффе-

Дифференциальное уравнение вида

ренциальное уравне-

y

f

y

.

ние первого порядка

x

в нормальной форме

93.

Однородный много-

Многочлен вида

Pn (x)

a1xk1 yl1

a2 xk2 yl2

,

член

если все его слагаемые имеют одну и ту же

суммарную степень: k1

l1

k2

l2

n .

94.

Односторонний пре-

См. левосторонний предел, правосторонний

дел

предел.

95.

Окрестность

Окрестностью точки a

называется любой

открытый интервал, содержащий точку a .

96.

Окружность

Линия второго порядка, каноническое уравне-

ние которой имеет вид

x2

y2

R2 .

97.

Определение произ-

Производной

функции

y f (x)

в

точке

x

водной

называется предел отношения приращения

функции к приращению аргумента, когда при-

ращение аргумента стремится к нулю.

y

dy

lim

y

.

dx

x

0

x

98.

Определенный инте-

b

n

f (x)dx

lim

f (

k )

xk .

грал

a

n

0 k

1

max

xk

№

Термин

Значение

п/п

99.

Определитель

Определителем квадратной матрицы называет-

a11

a12

a1n

ся число detA

A

a21

a22

a2n

, вычисляе-

an1 an2

ann

мое по определенному правилу.

100.

Ордината

Координата точки на оси Oy в прямоугольной

системе координат.

101.

Орт

См. единичный вектор

102.

Отделение корня

Нахождение интервала, в котором находится

уравнения

единственный корень уравнения.

103.

Отрицание

Высказывание

A ,

которое истинно, если A

ложно, и ложно, если

A истинно.

Логическая

операция отрицание соответствует логической

связке «не».

104.

Парабола

Линия второго порядка, каноническое уравне-

ние которой имеет вид

y2

2 px .

105.

Первообразная

Функция F (x)

называется первообразной для

функции f (x) ,

если

выполняется равенство

F (x) f (x) .

106.

Первый замечатель-

lim sin x

1 или lim

x

1.

ный предел

x

0

x

x 0 sin x

107.

Пересечение мно-

Множество

A

B ,

состоящее из

элементов,

жеств

принадлежащих A и B .

108.

Подмножество

Множество

B

называется

подмножеством

множества

A

( B

A ),

если

любой элемент

множества B принадлежит множеству A .

109.

Порядок дифферен-

Наивысший порядок производных, входящих в

циального уравнения

дифференциальное уравнение.

110.

Порядок производной

См. производные высших порядков.

111.

Последовательность,

Последовательность {yn } называется ограни-

ограниченная сверху

ченной сверху,

если существует число M та-

кое, что каждый элемент yn

этой последова-

тельности удовлетворяет неравенству yn M .

№

Термин

Значение

п/п

112.

Последовательность,

Последовательность {yn } называется ограни-

ограниченная снизу

ченной снизу, если существует число m такое,

что каждый элемент

yn

этой последовательно-

сти удовлетворяет неравенству yn

m .

113.

Правая тройка век-

Тройка некомпланарных векторов a , b , c ,

торов

приведенных к общему началу, называется

правой,

если из конца вектора c

видно,

что

кратчайший поворот от вектора a к вектору b

происходит против часовой стрелки.

114.

Правило Лопиталя

Метод нахождения

пределов

функций,

рас-

крывающий

неопределѐнности

вида

0

и

0

. Обосновывающая метод теорема утвер-

ждает, что при некоторых условиях предел от-

ношения функций равен пределу отношения

их производных.

115.

Правильная рацио-

Рациональная дробь, степень числителя кото-

нальная дробь

рой меньше степени знаменателя.

116.

Правосторонний пре-

lim f (x)

lim f (x)

f (a

0) .

дел функции

x a

x

a 0

x a

117.

Предел последова-

Число a , к которому сходится последователь-

тельности

ность {yn }.

118.

Предел функции

Число b

является пределом функции

f (x)

при x

a,

если для любого

0 существует

проколотая окрестность точки a , в которой

выполняется

неравенство

f (x)

b

.

lim f (x)

b .

x a

119.

Предикат

Предложение, которое содержит переменные и

становится

высказыванием

при

подстановке

вместо переменных их значений.

120.

Признак Даламбера

Если для знакоположительного ряда

un

су-

сходимости знакопо-

n 1

ложительного ряда

un 1

ществует предел lim

D , то:

un

n

1) при D

1 ряд сходится;

2) при D

1 ряд расходится.

№

Термин

Значение

п/п

121. Признак интеграль-

Пусть члены знакоположительного ряда

un

ный сходимости зна-

n 1

коположительного

являются значениями некоторой непрерывной

ряда

положительной функции

f (x) , убывающей на

интервале x

[1, ) , так что un

f (n) . Тогда

1) если несобственный интеграл

f (x)dx

схо-

1

дится, то и ряд сходится;

2) если несобственный интеграл

f (x)dx

рас-

1

ходится, то и ряд расходится.

122. Признак Коши схо-

Если для знакоположительного ряда

un

су-

димости знакополо-

n 1

жительного ряда

ществует предел lim n u

n

K , то:

n

lim

un

a

0 ,

vn

n

то ряды

un и

vn

одновременно сходятся

n 1

n 1

126.

Приращение функ-

Приращение функции y

f (x) в точке x – это

ции

функция приращения аргумента x :

y f (x

x) f (x) .

127.

Производная

Основное понятие дифференциального исчис-

ления, характеризующее скорость изменения

функции (в данной точке).

№

Термин

Значение

п/п

128.

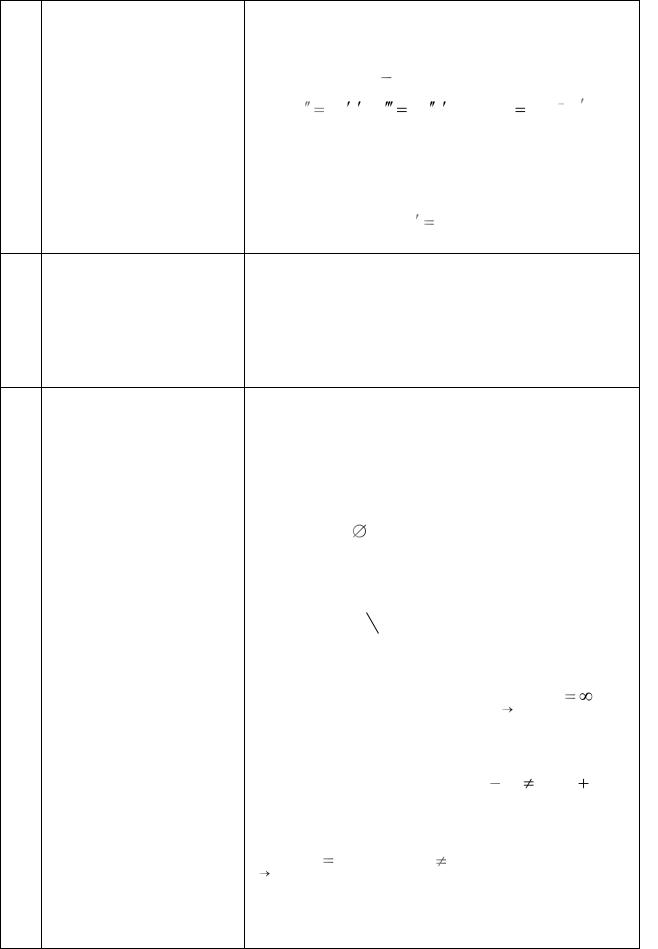
Производные выс-

Производная n -го порядка это производная от

ших порядков

производной (n

1) -го порядка:

y ( y ) , y

( y ) , ..., y(n) ( y(n 1) ) .

Число n называется порядком производной.

129.

Проколотая окрест-

Окрестность точки a , из которой удалена сама

ность

точка a .

130.

Простейшее диффе-

Дифференциальное уравнение вида

ренциальное уравне-

y f (x) .

ние

стве

точке O, которая называется началом коорди-

нат, на каждой оси выбраны положительные

направления и единицы измерения (орты).

O, которая называется началом координат, на

каждой оси выбраны положительные направ-

ления и единицы измерения (орты).

133.

Пустое множество

Множество , не содержащее ни одного эле-

мента.

134.

Радиус-вектор

Вектор, идущий из начала координат в данную

точку.

135.

Разность множеств

Множество A B , состоящее из элементов A ,

не принадлежащих B .

136.

Разрыв второго рода

Точка x0

называется

точкой бесконечного

(бесконечный)

разрыва функции f (x) , если lim f (x)

.

x

x0

137.

Разрыв первого рода

Точка x0

называется точкой скачка функции

(скачок)

f (x) , если односторонние пределы существу-

ют, но не равны, то есть

f (x0

0) f (x0

0) .

138.

Разрыв устранимый

Точка x0

называется

точкой устранимого

разрыва

функции f (x) , если существует

lim f (x)

b , но f (x0 )

b или

f (x0 ) не суще-

x x0

ствует.

139.

Разрыва точки

Точки, в которых нарушено условие непре-

рывности функции.

№

Термин

Значение

п/п

140.

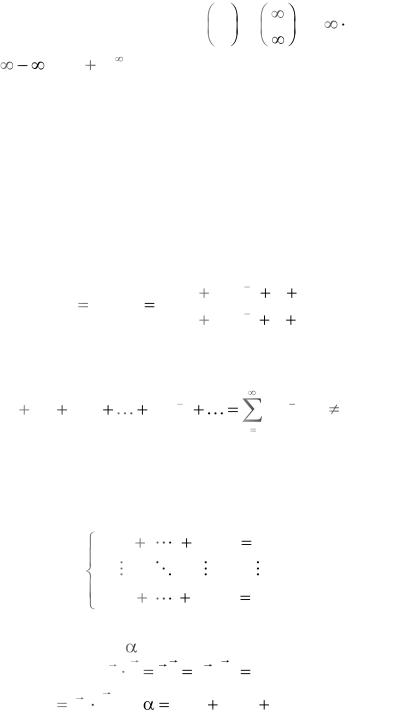
Раскрытие неопреде-

Методы вычисления пределов функций, задан-

ленности

ных формулами, которые в результате фор-

мальной подстановки в них предельных значе-

ний аргумента теряют смысл, то есть перехо-

дят

в выражения

типа:

0

,

, (

0) ,

0

(

) ,

(1

0) , …, по которым невозможно

судить о том, существуют или нет искомые

пределы (неопределенности).

141.

Расходящаяся после-

Последовательность, не являющаяся сходя-

довательность

щейся.

142.

Расходящийся ряд

Если последовательность N-х частичных сумм

{SN } ряда при неограниченном росте номера

N не стремится к конечному пределу, то ряд

называется расходящимся.

143.

Рациональная дробь

Отношение двух многочленов

Q (x)

b xm

b xm 1 ...

b

f (x)

m

0

1

m

.

a xn

a xn 1

P (x)

...

a

n

0

1

n

144.

Решение дифферен-

Функция,

обращающая

дифференциальное

циального уравнения

уравнение в тождество.

145.

Ряд бесконечной гео-

aq2

aqn 1

aqn 1 , a

метрической прогрес-

a

aq

0 .

сии

n 1

146.

Ряд Фурье

Тригонометрический ряд, коэффициенты, ко-

торого определены формулами Эйлера-Фурье.

147.

Система линейных

Система m линейных уравнений с n неизвест-

алгебраических

ными

уравнений

a11 x1

a1n xn

h1 ,

am1 x1

amn xn

hm .

148.

Скалярное произве-

Число, равное произведению модулей векторов

дение векторов

на косинус угла

между ними

a b

ab (a,b )

a

b

cos

x1 x2

y1 y2

z1 z2 .

№

Термин

Значение

п/п

149.

Смешанное произве-

Смешанным

произведением трех векторов

дение векторов

a,b,c называется скалярное произведение век-

тора a

b на вектор c .

x1 y1 z1

abc (a b ) c

x2 y2 z2

.

x3 y3 z3

150.

Степенной ряд

Бесконечная сумма степенных функций:

a (x

x )n .

n

0

n 0

151.

Сумма ряда

Число S , к которому стремится последова-

тельность его N-х частичных сумм {SN } при

неограниченном росте номера N.

152.

Сумма ряда беско-

a

нечной геометриче-

S

,

q

1.

q

ской прогрессии

1

153.

Сходящаяся последо-

Последовательность {yn } называется сходя-

вательность

щейся, если существует такое вещественное

число

a ,

что последовательность {yn a} яв-

ляется бесконечно малой последовательно-

стью.

154.

Сходящийся ряд

Ряд называется сходящимся, если последова-

тельность его N-х частичных сумм {SN } при

неограниченном росте номера N стремится к

конечному пределу lim SN

S .

N

155.

Точка максимума

Точка

x0

называется точкой максимума

функции

f (x) , если для всех точек x из неко-

торой окрестности точки x0

выполняется нера-

венство f (x0 )

f (x) .

156.

Точка минимума

Точка x0 называется точкой минимума функ-

ции f (x) , если для всех точек x из некоторой

окрестности

точки

x0

выполняется неравен-

ство f (x0 )

f (x) .

157.

Точка перегиба

Точка, лежащая на графике функции и разде-

ляющая выпуклую и вогнутую части графика.

158.

Точка сходимости

Значение, при котором функциональный ряд

функционального ря-

сходится.

да