Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский кооперативный институт (филиал РУК)

Предмет:

Макроэкономическое планирование и прогнозирование

Файл:

МатАн_ЛинАлг_080100 / Лекции_Математика_1_Линейная_алгебра

.pdf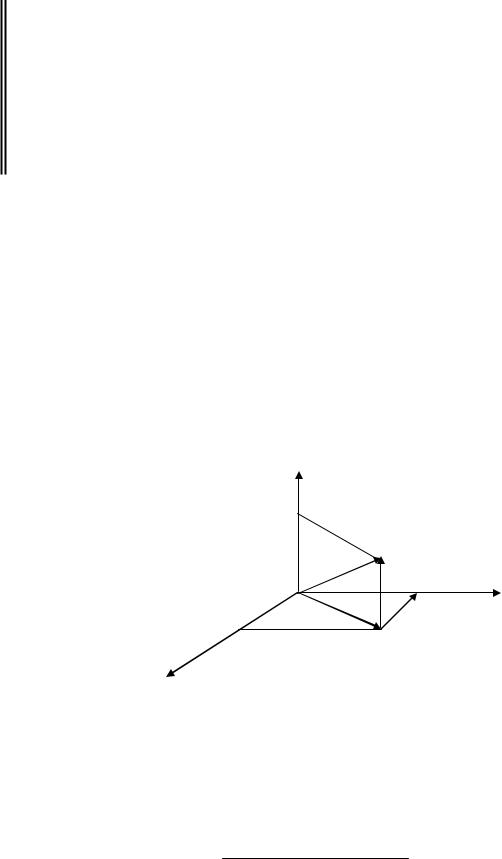

Скачиваний:

Добавлен:

26.02.2016

Размер:

454.39 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

взятые в определенном порядке.
Если e1, e2 , e3	– базис в пространстве и
	a = a1 e1 + a2 e2 + a3 e3 ,	(9)
то числа a1, a2 , a3	называются компонентами или координатами вектора a в

этом базисе, а представление (9) – разложением вектора a по базису.

В качестве примера рассмотрим декартову прямоугольную систему ко-

ординат в пространстве 3 . Она образована тремя взаимно перпендикуляр-

ными осями, имеющими общее начало координат O:		Ox – ось абсцисс, Oy –
ось ординат, Oz – ось аппликат (оси координат).
Любая точка в 3 имеет три координаты M (x , y		0	, z	0	).
	0	0		0
Тройка ортов i , j, k образует базис в пространстве 3.
Векторы i , j, k линейно независимые.
Рассмотрим вектор OM в 3 ,	где M (x, y, z) конец вектора
z
z	C
	M
	B
0	y				y
0					y

РИС. 2.1.13

Представим вектор OM в виде суммы векторов, лежащих на осях координат:


OM = OM1 + M1M = OA + OB + OC = xi					+ yj	+ zk .
Тогда
						(10)

	OM	= x × i	+ y × j	+ z × k

Записывают также OM = (x, y, z).

Частный случай, в 2 имеем a = (x, y) = x × i + y × j. 21

2.1.3. Линейные операции над векторами в координатах. Длина и направляющие косинусы вектора

Рассмотрим векторы, заданные в координатах.

a = (x , y z ),			b = (x , y	2	, z	2	).
1	1,	1	2	2		2

Решим ряд задач, связанных с этими векторами в координатах, учитывая свойства проекции вектора.

1) Модулем (длиной) вектора a называется положительное число

a = x12 + y12 + z12 .

Эта формула вытекает из свойства диагонали прямоугольного параллелепипеда.

2) Условие равенства векторов:

a = b x1 = x2 , y1 = y2 , z1 = z2 .

3) Линейные операции над векторами:

a + b = (x1 + x2 , y1 + y1 + y2 , z1 + z2 ),

λa = (λx1, λy1, λz1 ).

a − b = (x1 − x2 , y1 − y2 , z1 − z2 )

4)Направляющими косинусами вектора a называются косинусы углов α, β, γ , которые образует вектор a с осями координат Ox, Oy,Oz соот-

ветственно:

	x		y		z
cos α =	1	, cosβ =	1	, cos γ =	1	.
	a		a		a

Вектор a0 = (cos α, cosβ, cos γ) - единичный вектор, называемый ортом

вектора a.

5) Условие коллинеарности векторов a, b :

		x		y		z
a	b	1	=	1	=	1	= λ a	= λb.
a	b	x2	=	y2	=	z2	= λ a	= λb.
		x2		y2		z2

6)Координаты вектора AB по известным координатам начала A(xA , yA , zA ) и конца B(xB , yB , zB ) вектора:

Пример 13.	AB = (xB − xA , yB − yA , zB − zA )
Пример 13.	Даны точки:
	A(1,1,1), B(2, − 1,1), C(−2, 0, − 1).
Найти вектор	2 AB − 3AC.
Решение.
	22

AB = (1, − 2, 0) 2 AB = (2, − 4, 0),

AC = (−3, − 1, − 2) 3AC (−9, −3, −6),

2 AB − 3AC = (11, − 1, 6).

2.1.3.1. Задача о делении отрезка в данном отношении.

Даны точки A(xA , yA , zA ) и B(xB , yB , zB ).

Найти координаты точки M (x0 , y0 , z0 ), которая делит отрезок AB в от-

ношении λ , то есть

AM = λ .

A M B

Решение. Векторы

AM = (x0 − xA , y0 − yA , z0 − zA ),

MB = (xB − x0 , yB − y0 , zB − z0 ).

коллинеарны, причем AM = λMB. В силу условия коллинеарности имеем

x0 − xA

y0 − yA

z0 − zA

= λ.

xB − x0

yB − y0

zB − z0

Откуда,

x − x = λ(x − x ) x + λx = x + λx x =

xA + λxB

0 A

B 0

1 + λ

Аналогично находятся y0 , z0 .

Итак,

x =

xA + λxB

, y =

yA + λyB

, z =

zA + λzB

1 + λ

Частный

случай: λ = 1,

точка M (x0 , y0 , z0 ) делит отрезок AB пополам:

x =

xA + xB

, y =

yA + yB

, z

zA + zB

2.2.Произведения векторов

2.2.1.Скалярное произведение векторов

2.2.1.1.Определение

Скалярным произведением a × b

двух векторов a и b

называется чис-

ло, равное произведению модулей векторов на косинус угла

(a,b) между ними

a × b =

cos(a,b )

Обозначается скалярное произведение также (a,b ) , ab .

Пример 14.

= 2,

= 3,

(a,b ) = 60° .

Найти скалярное произведение a b .

= 2 × 3 × cos 60° = 2

× 3 ×

= 3.

Решение. ab

2.2.1.2. Свойства скалярного произведения

	1)		Учитывая	(см.


b				a b =
		cos(a,b ) = Прa b , то

a b = b × Прb a;

2)a b = b a ;

3)(l a )b = l(a b );

4)(a + b )c = a c + b c ;

5)a a = a a cos 0 = a 2 ,

	Рис. 2.2.1), что	b
	Рис. 2.2.1), что

a	Пр b . Аналогично,
a	Пр b . Аналогично,
	a

Прa b a

Рис. 2.2.1

пишут также a 2 = a 2 и называют скалярным

квадратом вектора;

6) скалярное произведение двух ненулевых векторов равно нулю, тогда и только тогда, когда векторы перпендикулярны

ab = 0 a b .

Действительно:

а) если

a b , то (a,b ) = 90° cos(a,b) = 0 , следовательно

ab =

cos(a,b ) = 0;

б) если ab = 0 , то, учитывая, что

ab =

¹ 0 ,

¹ 0 , полу-

cos(a,b )

чим cos(a,b )

= 0 . Из этого следует, что (a,b) = ±90° a ^ b .

2.2.1.3. Выражение скалярного произведения в координатах

Получим выражение скалярного произведения векторов в координа-

тах

Пусть a = (x1, y1, z1 ) , b = (x2 , y2 , z2 ) .

Учитывая свойства 5 и 6 скалярного произведения, составим таблицу ска-


лярных произведений единичных векторов i ,													j , k .

							i	j		k
							1	0		0
						i		0		0
						i		1		0
						j	0	1		0
							0	0		1
					k		0	0		1
Отсюда имеем
Отсюда имеем
														+ z2k ) =
	ab = (x1i + y1 j				+ z1k )(x2i							+ y2 j		+ z2k ) =
																	2	+ z y			+
= x x ii		+ y x ji		+ z x ki + x y								ij + y y			2	j	2	+ z y	2	kj	+
1	2	1	2	1	2				1		2		1		2			1	2

+x1z2ik + y1z2 jk + z1z2k 2 = x1x2 + y1 y2 + z1z2 .

Итак, получим выражение скалярного произведения в координатах

ab = x1x2 + y1 y2 + z1z2 .

Пример 15. Дано: a = (1,0, −2) , b = (-1,1,3) .

Найти: ab , a 2 , a × (a - 2b ) .

Решение.

ab =1 × (-1) + 0 ×1 + (-2) × 3 = -7 ; a2 = a 2 =12 + (-2)2 = 5 ;

a(a - 2b ) = a × a - 2ab = a 2 - 2ab = 5 + 14 =19 .

2.2.1.4. Приложения скалярного произведения

Из определения и свойств скалярного произведения вытекают следующие

приложения скалярного произведения.

Длина вектора a = (x, y, z)

xx + yy + zz

x2 + y2 + z2

Угол γ между векторами a = (x1, y1, z1 ) , b = (x2 , y2 , z2 ) :

cos γ = cos(ab ) =

Условие перпендикулярности векторов

a, b :

Если вектора a, b перпендикулярны ( a b ), то по свойству 6 имеем, что

Расписывая скалярное произведение в координатах, получим

ab = 0 .

x1x2 + y1 y2 + z1z2 = 0 .

2.2.2.Векторное произведение двух векторов

2.2.2.1.Определения:

Тройка некомпланарных векторов a , b , c , приведенных к общему началу, называется правой, если из конца вектора c видно, что кратчайший пово-

рот от вектора a к вектору b происходит против часовой стрелки (Рис. 2.2.2).

Пример правой тройки: орты i ,			j , k	(Рис. 2.2.3).
c
			z			c
			k
a	b				y
a		x	i	j		b	a
		x	i	j		b	a
РИС. 2.2.2			РИС. 2.2.3			РИС. 2.2.4

Тройка a , b , c – левая, если поворот от a к b виден из конца вектора c

по часовой стрелке (Рис. 2.2.4).

b = ( x2 , y2 , z2 )

Векторным произведением векторов a и b называется вектор c (Рис. 2.2.5), удовлетворяющий трем условиям:

c a , c b ,

sin (a,b ),

c = a × b

3) a , b , c – правая тройка.		a
3) a , b , c – правая тройка.		b × a
	.	b × a
Обозначения векторного произведения: a × b , a,b	.
		РИС. 2.2.5
		РИС. 2.2.5

2.2.2.2. Свойства векторного произведения

1.a × b = −b × a . Смену знака легко увидеть из Рис. 2.2.4.

2.(la ) ´ b = l(a ´ b ).

3.(a + b )´ c = a ´ c + b ´ c .

4.a × a = 0 для любого вектора a , так как sin (a, a ) = sin 0° = 0 длина

вектора a × a равна нулю.

5.Векторное произведение двух ненулевых векторов равно нулю 0, тогда

итолько тогда, когда векторы коллинеарны

					.

	a	´ b	= 0 Û a	b
Условие a × b = 0 является условием коллинеарности векторов a и b .
2.2.2.3. Выражение векторного			произведения векторов a = ( x , y , z					) ,
				1		1	1

в координатах.

Учитывая определение и свойства векторного произведения, составим таблицу векторных произведений единичных векторов i , j , k (Рис. 6).

k			i	j	k
k

0		i	0	k	− j
i	j
i	j	j	−k	0	i
		j	−k	0	i

РИС. 2.2.6		k	j	−i	0

Стрелки показывают кратчайшее движение против часовой стрелки. Отсюда имеем

a × b = (x1i + y1 j + z1k ) × (x2i + y2 j + z2 k ) =


= x1x2i	× i + y1x2 j × i + z1x2k × i					+ x1 y2i	× j + y1 y2 j		× j +
			× k		× k + z1z2 k × k			= − y1x2k +
+ z1 y2 k × j		+ x1z2i	× k	+ y1z2 j	× k + z1z2 k × k			= − y1x2k +
							( y1z2
+z1x2 j	+ x1 y2k − z1 y2i			− x1z2 j	+ y1z2i =		( y1z2	− z1 y2 )i −

−( x1z2 − z1x2 ) j + ( x1 y2 − y1x2 )k .

Таким образом, имеем,

, −

a × b

Или, учитывая свойство разложения определителя по элементам строки, можно записать

× b

x2 y2 z2

Даны

Пример 16.

векторы: a = (2,0, −1), b = (1,1,3)

Найти: векторные произведения: a × b,

a × (a − 2b ).

Решение.

0 −1

, −

2 −1

2 0

= (1, −7, 2) ;

× b

1 1

a × (a −

−4) .

2b ) = a × a

− 2a × b

= 0 − 2a × b = (−2,14,

2.2.2.4. Приложения векторного произведения

1. Площадь треугольника ABC

Из геометрии известно, что

SABC

AB × AC × sin j (Рис. 2.2.7).

Переходя к векторам, получим

РИС. 2.2.7

(

)

SABC =

sin

AB, AC

AB ´ AC

2. Площадь параллелограмма

SABDC = 2SABC =

AB ´ AC

РИС. 2.2.8

3. Нахождение вектора, перпендикулярного двум данным

Даны векторы a , b .

Найти такой вектор c , чтобы c a , c b .

В силу определения векторного произведения в качестве вектора c

мож-

но взять вектор c = a × b .

4. Угол между векторами a и b

a ´ b

sin (a,b ) =

2.3.Комплексные числа

2.3.1.Комплексные числа, их изображение на плоскости. Модуль и аргумент комплексного числа

Введение комплексных чисел связано с развитием алгебры. Они возникли

всвязи с решением кубических уравнений и долгое время не находили приложений. Поэтому появились названия «мнимая единица», мнимое число» и т.п.

В настоящее время комплексные числа нашли широкое применение во многих науках.

2.3.1.1. Определения

Комплексным числом называется выражение z = x + iy , где x, y – дей-

ствительные числа, а i – новое число, обладающее свойством i2 = −1 и называ-

емое мнимой единицей. Число x называется действительной частью, y –

мнимой частью комплексного числа z . Они обозначаются x = Re z , y = Im z .

Множество комплексных чисел обозначается буквой .

Выражение z = x + iy называется алгебраической формой записи ком-

плексного числа. В дальнейшем мы познакомимся и с другими формами запи-

си.
Два комплексных числа z1 = x1 + iy1 и z2 = x2 + iy2					называются равными,
если равны их действительные и мнимые части,		то есть x1 = x2 и y1 = y2 . В
частности z = 0 , если x = y = 0 . Числа z = x + iy	и			= x − iy называются ком-
частности z = 0 , если x = y = 0 . Числа z = x + iy	и		z	= x − iy называются ком-
плексно-сопряженными.
2.3.1.2. Изображение комплексных чисел на плоскости
Комплексные числа изображаются точ-	y
Комплексные числа изображаются точ-	y
ками или векторами на плоскости. В декарто-	y					M (x, y)
вой системе координат каждому комплексному	y					M (x, y)
вой системе координат каждому комплексному					r
числу z = x + iy ставится в соответствие точка					r
числу z = x + iy ставится в соответствие точка					ϕ
M (x, y) или радиус-вектор OM = (x, y) с теми					ϕ

	O				x	x
же координатами.	O				x	x
же координатами.					РИС. 2.3.1

Обычные действительные числа можно рассматривать как частный случай комплексных чисел, у которых мнимая часть равна нулю Im z = 0 . Все точки, изображающие действительные числа, будут лежать на оси Ox . Поэтому ось Ox называют действительной осью.

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

Соседние файлы в папке МатАн_ЛинАлг_080100

#
26.02.2016483.32 Кб41ЗаданияСР_ЛА_080100.pdf
#
26.02.2016690.03 Кб41ЗаданияСР_МА_080100.pdf
#
26.02.2016869.89 Кб49ЛА_экз_1курс_экономика_заочн.doc
#
26.02.2016454.39 Кб44Лекции_Математика_1_Линейная_алгебра.pdf
#
26.02.2016494.69 Кб51Лекции_Математика_2_Дифференциальное исчисление.pdf
#
26.02.2016573.11 Кб48Лекции_Математика_3_Интегральное исчисление.pdf
#
26.02.20161.52 Mб59МА_экз_1курс_экономика_заочн.doc
#
26.02.2016855.38 Кб43Математика_Словарь терминов.pdf
#
26.02.2016630.28 Кб47ПланыПЗ_ЛА_080100.pdf