МатАн_ЛинАлг_080100 / Лекции_Математика_1_Линейная_алгебра

1.3.Системы линейных алгебраических уравнений

1.3.1.Системы линейных алгебраических уравнений

1.3.1.1.Определения

Зададим систему из n линейных уравнений с n неизвестными

ее коэффициентов.

Нас будет интересовать вопрос о разрешимости системы (3) для каждой системы чисел (h1,..., hn ) .

Система чисел (x1,..., xn ) называется решением системы уравнений (3),

если числа xi удовлетворяют этим уравнениям.

1.3.2.Метод Крамера решения систем линейных уравнений

1.3.2.1.Метод Крамера

Если определитель матрицы A не равен нулю:

то система (3) для любой системы чисел (h1,..., hn ) имеет единственное реше-

ние, вычисляемое по формулам Крамера2:

1.3.3. Матричный метод решения систем линейных уравнений

Существует метод решения системы линейных уравнений

основанный на использовании обратной матрицы. Этот метод называется мат-

ричным методом.

Рассмотрим этот метод на примере системы трех уравнений

Данный метод состоит из следующих этапов: 1. Составим три матрицы

Назовем A – матрицей системы, H – матрицей свободных членов, X – матрицей решений.

Система уравнений запишется в матричном виде

A × X = H .

2. Пусть A – невырожденная матрица. Тогда найдем обратную матрицу

A−1 .

3. Найдем матрицу решений по формуле

X = A−1 × H .

Эта формула следует из рассуждений

AX = H A−1 AX = A−1H EX = A−1H X = A−1H .

Пример 9. Решить матричным методом систему

Решение.

1. Составим три матрицы

изапишем систему в виде AX = H.

2.Найдем обратную матрицу (см. пример из прошлой лекции): а) Найдем определитель матрицы

1 0 2

A = 2 −1 3 = −2 + 4 − 3 = −1.

0 1 2

б) Найдем алгебраические дополнения

13

и составим матрицу

в) Найдем транспонированную матрицу

г) Найдем обратную матрицу

1.3.4. Метод Гаусса решения систем линейных уравнений

Рассмотрим еще один метод решения систем линейных уравнений, основанный на использовании матриц – метод Гаусса (метод исключения неизвестных). Рассмотрим его на примере системы трех уравнений.

Метод Гаусса решения системы

состоит из следующих этапов:

1. Составим расширенную матрицу системы, добавив столбец свободных членов

14

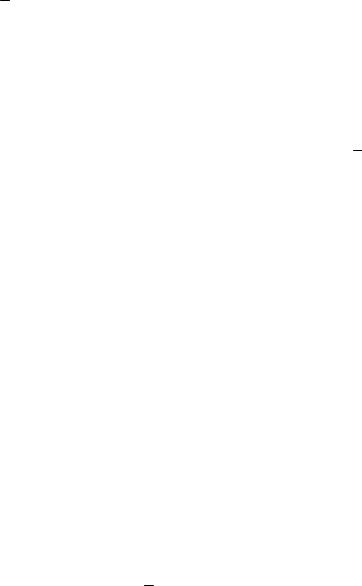
2. Преобразуем матрицу A к треугольному виду с помощью элементарных преобразований строк

3. Запишем систему линейных уравнений, соответствующих матрице B

и решим ее. Решение этой системы является также решением заданной системы.

Пример 10. Решить методом Гаусса систему уравнений

x + 2z = −5,

2x − y + 3z = −10,

Решение. Составим расширенную матрицу и преобразуем ее к треугольному виду

Запишем систему с расширенной матрицей B и решим ее

15

Тема 2. Векторная алгебра

2.1. Векторы. Линейные операции над векторами

Понятие вектора возникло в XIX в. в связи с потребностями механики и физики. Основы векторного исчисления заложены английским математиком Гамильтоном и немецким математиком Грассманом.

2.1.1. Векторы. Линейные операции над векторами. Проекция вектора на ось

2.1.1.1. Определения

Вектором называется отрезок, которому приписано определенное направление, т.е. указаны начало и конец отрезка.

B

a

Обозначается: a или AB , где

A – начало, B – конец вектора.

A

РИС. 2.1.1

Модулем (длиной) вектора называется длина отрезка и обозначается

a , AB

Вектор, модуль которого равен нулю, называется нулевым вектором 0 . Нулевой вектор направления не имеет.

Вектор, модуль которого равен единице, называется единичным векто-

ром или ортом e направления, указанного этим вектором.

Векторы называются компланарными, если они лежат в одной плоскости или параллельны ей.

Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Обозначается a b .

16

При этом коллинеарные векторы могут быть одинаково направленны-

Из этого определения следует, что при параллельном переносе вектора, получается вектор, равный исходному. Поэтому начало вектора можно помещать в любую точку пространства, а вектор называют свободным.

В некоторых науках рассматриваются также скользящие векторы, которые можно перемещать вдоль прямой и связанные векторы, начало которых фиксировано.

2.1.1.2. Линейные операции над векторами

Введем линейные операции над векторами.

1. Суммой векторов a и b называется вектор a + b, для построения ко-

торого существует два правила:

а) правило треугольника: a + b лежит на стороне треугольника, постро-

енного на векторах a, b , имеет начало, совпадающее с началом вектора a, а

конец в конце вектора b (Рис. 2.1.4);

б) правило параллелограмма: a + b – диагональ параллелограмма, по-

строенного на векторах a, b , как на сторонах (Рис. 2.1.5).

17

b

a

Свойства:

a + b = b + a ,

(a + b ) + c = a + (b + c ) .

2. Суммой нескольких векторов a + b + c + d называется вектор, который строится по правилу многоугольника: это вектор, замыкающий ломаную линию, составленную из слагаемых векторов.

b

c

a

a + b + c + d d

РИС. 2.1.6

3. Разностью векторов a и b называется вектор a − b = a + (−1)b, кото-

рый можно построить следующим образом:

a − b

b

a

РИС. 2.1.7

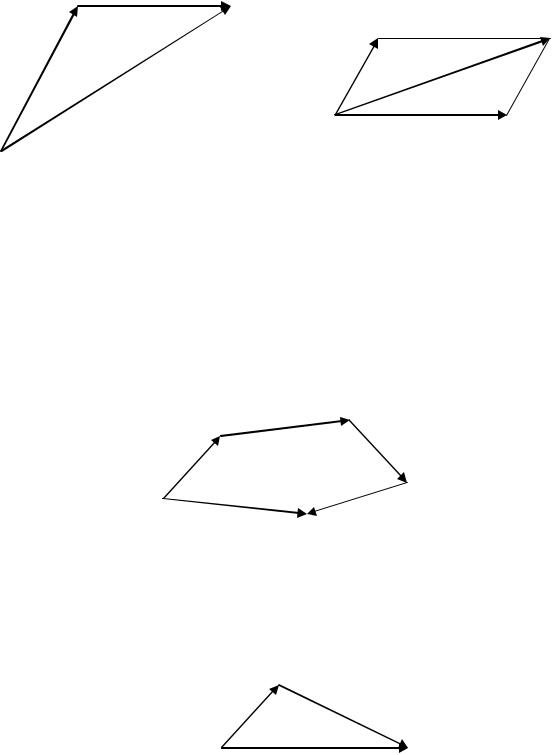
4. Произведением вектора a на число λ называется вектор, удовлетворяющий условиям:

18

1)l a = l × a

2)l a -- a если λ > 0 , l a -¯ a если λ < 0 .

Пример 11.

Свойства:

l(a + b ) = la + lb , (l + m)a = la + ma , l(ma ) = (lm)a .

2.1.1.3. Проекция вектора

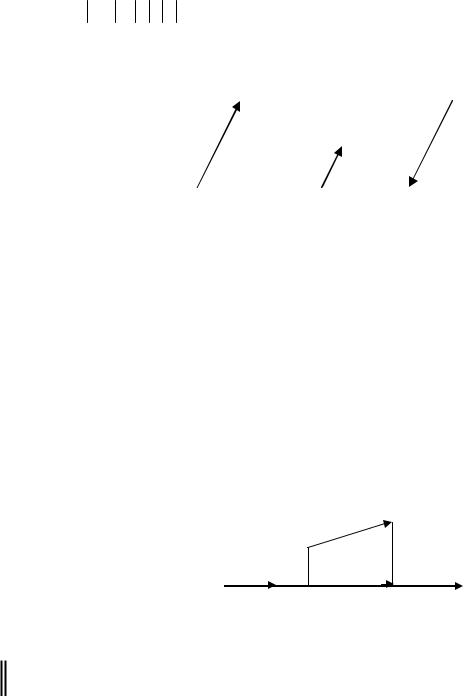
Пусть дан вектор AB и ось Ou (прямая с направлением, заданным ортом e и началом координат O ) (Рис. 2.1.9).

Найдем проекции точек A и B на ось Ou - это точки A′, B′.

Построим вектор A¢B¢ .

Проекцией вектора AB на ось Ou называется число

19

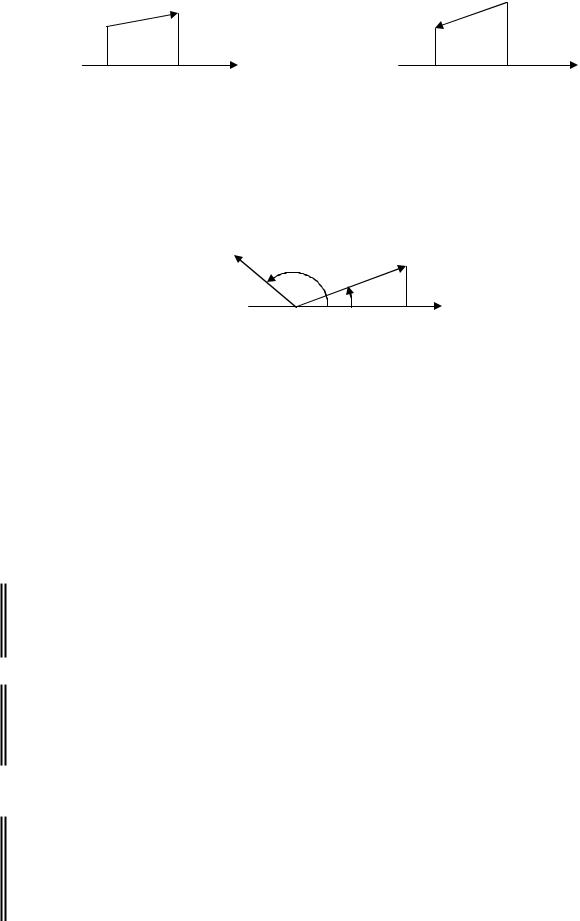
Пример 12.

РИС. 2.1.12

2.ПрOu (a ± b ) = ПрOu a ± ПрOub .

3.ПрOu λa = λПрOu a .

2.1.2. Линейная зависимость и независимость векторов. Базис. Разло-

жение вектора по базису. Координаты вектора

2.1.2.1. Линейная зависимость и независимость векторов

Система векторов a, b , c называется линейно зависимой, если один век-

тор можно выразить как линейную комбинацию других.

a = λ1b + λ2c.

Система векторов a, b , c называется линейно независимой, если равен-

ство λ1a + λ2b + λ3c = 0 выполняется только при λ1 = λ2 = λ3 = 0.

2.1.2.2. Базис. Разложение вектора по базису. Координаты вектора

Базисом в пространстве 3 называются любые 3 некомпланарные вектора, взятые в определенном порядке.

Базисом на плоскости 2 называются любые 2 неколлинеарные вектора, 20