
МатАн_ЛинАлг_080100 / Лекции_Математика_2_Дифференциальное исчисление
.pdf
Если f ′(x) < 0 при x (a,b) , то функция f (x) убывает на интервале
(a,b) .
Доказать самостоятельно.
2.3.2. Точки экстремума. Необходимое условие экстремума
Определения.
1) Точка x0 называется точкой максимума функции f (x) , если для всех точек x из некоторой окрестности точки x0 выполняется неравенство
f(x0 ) > f (x) (Рис. 2.3.3).
2)Точка x0 называется точкой минимума функции f (x) , если для
всех точек x из некоторой окрестности точки
f (x0 ) < f (x) (Рис. 2.3.4).
y |
|
|
|
y |
|
|
|
y = f (x) |
|
|
|
f (x0 ) |
|
|
|
|
f (x) |
|
|
0 |
x |
x0 |
x |
0 |
|
|
f (x0 ) > f (x) |
|
|
x0 выполняется неравенство
y = f (x)
f (x) f (x0 )
x |
x0 |
x |
f (x0 ) < f (x)
РИС. 2.3.3 |
РИС. 2.3.4 |
Значение функции |
f (x0 ) в точке максимума (минимума) называется мак- |
симумом (минимумом) функции и обозначается max f (x) ( min f (x) ).
Точки максимума и минимума называются точками экстремума функции f (x) , а значение функции в них называется экстремумом функции extr f (x) .
31
y |
|
|
y = x3 |
0 |
x |
РИС. 2.3.5 |
|
Теорема (необходимое условие экстремума)
Если x0 - точка экстремума дифференцируемой
функции f (x) , то f ′(x0 ) = 0 .
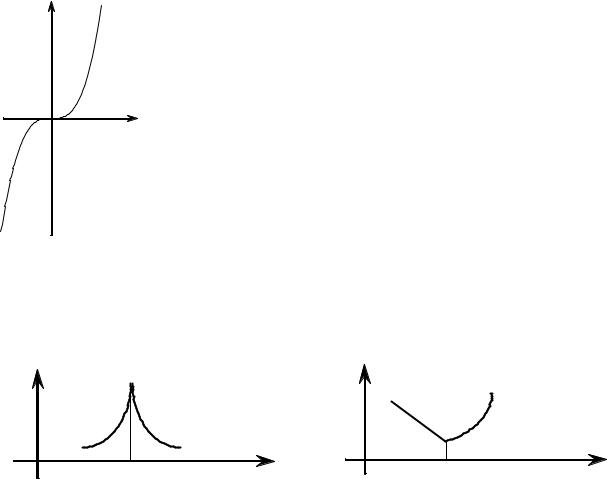
Замечание 1. Данное необходимое условие не является достаточным. То есть, из условия f ′(x0 ) = 0 не
следует, |
что x0 - точка экстремума функции. Например, |
функция |
f (x) = x3 имеет производную f ′(x) = 3 x2 . При |
x = 0, f ′(0) = 0 . Но точка x = 0 , как видно из графика функции f (x) (Рис. 2.3.5) не является точкой экстрему-
ма.
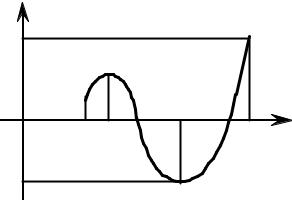
Замечание 2. Функция f (x) может принимать экстремальное значение в точках, где f ′(x) не существует (Рис. 2.3.6, Рис. 2.3.7).
y |
y |
y = f (x)
y = f (x)
0 |
x |
x |
0 |
x |
2 |
x |
1 |
|
|
||||
|
f ′(x1 ) = ∞ |
|
|
f ′(x2 ) - не существует |
|
|
|
РИС. 2.3.6 |
|
|
РИС. 2.3.7 |
|
|
Такие экстремальные точки называются точками острого экстремума (в |
||||||
отличие от точек гладкого экстремума, где f ′(x) = 0 ). |
|
|
||||
Поэтому необходимое условие экстремума можно сформулировать так: |
||||||
если x0 |
- точка экстремума функции |
f (x) , то |
f ′(x0 ) равна нулю или не суще- |
|||
ствует.
Определение. Точка x0 , в которой f ′(x0 ) равна нулю или не существу-
ет, называется критической точкой функции f (x) .
Итак, если x0 - точка экстремума, то x0 - критическая точка, но не наобо-
рот. Если x0 - критическая точка, то она не обязательно точка экстремума.
32
2.3.3. Достаточный признак существования экстремума |
|
Теорема. Если x0 - критическая точка функции f (x) |
и производная |
f ′(x) при переходе аргумента через эту точку меняет знак, |
то x0 - точка |
экстремума функции f (x) . |
|
Причем, если при переходе слева направо знак меняется с плюса на минус,
то x0 - точка максимума, если с минуса на плюс, то точка минимума.
2.3.3.1. Схема исследования функции на возрастание, убывание и экстре-
мумы
Задача.
Дана функция f (x) . Найти интервалы монотонности и экстремумы
функции.
Схема решения задачи:
1.Найти область определения Dy функции f (x) .
2.Найти f ′(x) , найти критические точки, решив уравнение f ′(x) = 0 и
выделив точки, где f ′(x) не существует.
3.Разбить область определения на интервалы критическими точками и точками разрыва и определить знак производной в каждом из них. Сделать вывод: по знаку производной определить интервалы монотонности и точки экстремума.
4.Найти экстремумы функции.
Пример. Найти интервалы монотонности и экстремумы функции
y = x2 e− x .
Решение.
1.Dy = (−∞ , ∞) .
2.y′ = 2x × e− x - x2 × e− x = x × (2 - x) × e− x ,
y′ = 0 x × (2 - x) × e− x = 0 x1 = 0, x2 = 2 - критические точки.
33
3.
|
x |
(−∞, 0) |
|
0 |
(0, 2) |
|
2 |
(2, ∞) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ′(x) |
− |
|
0 |
+ |
|
0 |
− |
||
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
|
|
min |
|
|
max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На интервалах (−∞, 0), (2, ∞) |
функция убывает, на интервале (0, 2) функ- |
|||||||||
ция возрастает. Точки x1 = 0 - точка минимума, |
x2 = 2 - точка максимума. |
|||||||||
4. min f (x) = f (0) = 0 , max f (x) = f (2) = |
4 |
. |
|
|
||||||
|
|
|
||||||||
|
|
|
|
|
|
e2 |
|
|
||
2.3.3.2. Наибольшее и наименьшее значение функции на отрезке.
Экстремумы функции носят локальный характер, т.е. max f (x) , min f (x) -
это наибольшее и наименьшее значения функции в некоторой окрестности точки экстремума. Функция может иметь несколько максимумов и минимумов.
Рассмотрим глобальную задачу о нахождении наибольшего и наименьшего значения непрерывной функции на отрезке (замкнутом интервале).
Задача. Дана непрерывная на [a, b] функция f (x) . Требуется найти наибольшее M и наименьшее m значения функции f (x) на этом отрезке.
Решение. Из чертежа (Рис. 2.3.8) видно, что наибольшее и наименьшее значения функция принимает либо в точках экстремума, либо на концах отрезка.
y
M
y = f (x)
x 2
0 |
а x1 |
b x |
m
РИС. 2.3.8
Отсюда вытекает схема решения задачи:
1. Найти y′ , решить уравнение y′ = 0 , найти критические точки, лежащие
внутри отрезка [a, b] .
34
2.Найти значение функции в этих точках и на концах интервала.
3.Выделить среди этих значений наибольшее и наименьшее.
Пример. Найти наибольшее и наименьшее значения функции
y = x5 - 5x4 + 5x3 + 3 на отрезке [−1, 2] .
Решение.
1. y′ = 5x4 - 20x3 + 15x2 = 5x2 × (x2 - 4x + 3) ,
y′ = 0 5x2 × (x2 - 4x + 3) = 0 x1 = 0, x2 = 1, x3 = 3 ,
точку x3 = 3 не рассматриваем, т.к. 3 [−1, 2].
2. Находим: f (0) = 3, f (1) = 4, f (−1) = −8, f (2) = −5 .
3. Сравнивая полученные значения функции делаем вывод: наибольшее значение M = 4 = f (1) ,
наименьшее значение m = −8 = f (−1) .
2.3.4. Исследование функции на выпуклость, вогнутость, точки перегиба
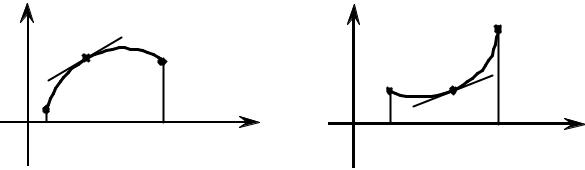
1) График функции f (x) называется выпуклым на интервале (a,b) , если он лежит под касательной, проведенной к графику в любой точке интервала
(a,b) (Рис. 2.3.9).
2) График функции f (x) называется вогнутым на интервале (a,b) , если он лежит над касательной, проведенной к графику в любой точке интервала
(a,b) (Рис. 2.3.10).
35
y |
y |
y = f ( x) |
y = f (x) |
0 а |
b |
x |
0 |
а |
b |
x |
РИС. 2.3.9 |
РИС. 2.3.10 |
Теорема. (Достаточное условие выпуклости, вогнутости графика функ-
ции).
1)Если f ′′(x) < 0 на (a,b) , то график функции f (x) выпуклый на (a,b) ;
2)Если f ′′(x) > 0 на (a,b) , то график функции f (x) вогнутый на (a,b) .
2.3.4.1. Точки перегиба
Определение. Точка M (x0 , y0 ) , лежащая на графике функции, называет-
ся точкой перегиба, если она разделяет выпуклую и вогнутую части графика
(рис.6.).
Теорема 1 (необходимое условие перегиба).
Если M 0 (x0 , y0 ) - точка перегиба графика функции f (x) , то f ′′(x0 ) либо равна нулю, либо не существует.
Теорема 2 (достаточное условие перегиба)
Если f ′′(x0 ) = 0 или f ′′(x0 ) не существует и при переходе x через точку x0 вторая производная f ′′(x) меняет знак, то точка M 0 (x0 , y0 ) , y0 = f (x0 ) яв-
ляется точкой перегиба графика непрерывной функции f (x) .
2.3.4.2. Схема исследования графика функции на выпуклость, вогну-
тость, точки перегиба
Задача. Дана функция f (x) . Найти интервалы выпуклости и вогнутости графика функции, точки перегиба.
Схема решения задачи:
36
1. Найти область определения Dy функции f (x) .
2. Найти f ′(x), f ′′(x) , решить уравнение f ′′(x) = 0 и выделить точки, где
f ′′(x) не существует. Найти критические на перегиб точки.
3. Разбить область определения функции критическими точками и точками разрыва на интервалы и найти знак f ′′(x) в каждом интервале. Сделать вы-
вод: найти интервалы выпуклости, вогнутости.
4. Найти вторые координаты точек перегиба, записать эти точки.
Пример. |
Найти интервалы выпуклости, |
|
вогнутости и точки перегиба |
|||||||
графика функции y = x4 - 6x2 + 5 . |
|
|
|
|
|
|
||||
Решение. |
|
|
|
|
|
|
|
|
|
|
1. Dy = (−∞, ∞) . |
|
|
|
|
|
|
|
|||
2. y′ = 4x3 - 12x , y′′ = 12x2 - 12 |
|
|
|
|
|
|
||||
|
y′′ = 0 12 × (x2 - 1) = 0 x1 = -1, x2 = 1 - критические |
на перегиб |
||||||||
точки. |
|
|
|
|
|
|
|
|
|
|
3. |
|
|
|
|
|
|
|
|
|
|
|
x |
(-¥, -1) |
|
-1 |
(-1, 1) |
|
1 |
(1, ¥) |
|
|
|
f ′′(x) |
+ |
|
0 |
− |
|
0 |
|
+ |
|
|
f (x) |
вогнут. |
т. перегиба |
выпукл. |
|
т. перегиба. |
вогнут. |
|
||
|
|
|
|
|
|
|
|
|||
График вогнутый на (-¥, -1) , (1, ¥) , график выпуклый на (-1, 1). |
||||||||||
4. f (−1) = 0, f (1) = 0, |
M1 (−1, 0), M 2 (1, 0) |
- точки перегиба. |
|
|
||||||
2.4.Частные производные функции двух переменных. Градиент
Впрактике часто встречаются функциональные зависимости от нескольких переменных величин. Например, площадь S прямоугольника со сторонами x, y зависит от двух переменных S = x × y.
2.4.1. Функции двух переменных, область определения
В терминах переменных величин определение функции двух переменных можно сформулировать следующим образом:
Переменная z называется функцией двух независимых переменных x, y если каждой паре ( x, y ) значений этих переменных из некоторого заданно-
37
го множества пар D по определенному правилу ставится в соответствие некоторое действительное число z.
Обозначение функции двух переменных z = f ( x, y ).
Пара значений независимых переменных ( x, y ) определяет некоторую
точку плоскости XOY . Поэтому D − область определения функции двух переменных – это некоторое множество точек плоскости XOY . Обычно областью определения является часть плоскости XOY , ограниченная одной или несколь-
кими линиями.
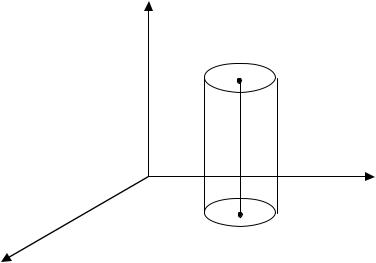
Для геометрической интерпретации функции z = f ( x, y ) рассматрива-
ется система координат Oxyz. Каждой точке M ( x, y ) D ставится в соответ-
ствие точка пространства N ( x, y, f ( x, y )) .
Обычно графиком функции двух переменных является некоторая по-
верхность.
Поверхность является графиком тогда, когда каждая прямая, параллельная оси Oz пересекает поверхность на более, чем в одной точке.
z
|
N |
|
z = f ( x, y ) |
0 |
y |
x |
D M ( x, y ) |
РИС. 2.4.1
2.4.2. Частные производные функции двух переменных
Если у функции двух переменных z = f ( x, y ) зафиксировать переменную y ( y = y0 ), то z станет функцией одной переменной z = f ( x, y0 ) .
38

Определение. |
Производная функции z = f ( x, y ) |
по переменной x при |
|||||||||||
условии, |
что |
y |
- |
постоянная |
величина, |
называется |
частной производной |
||||||
|
f ( x, y ) |
|
|
|
|
|
∂z |
∂f |
′ |
′ |
|||
|
|
|
|
|
|
|
|
|
|||||
функции |
по x и обозначается |
; |
|
||||||||||
; zx ( x, y); fx ( x, y ). |
|||||||||||||
|
|
|
|
|
|
|
|
∂y |
∂y |
|
|
|
|
Аналогичным образом вводится понятие частной производной функции |
|||||||||||||
z = f ( x, y ) по y. |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
∂z |
∂f |
′ |
|
′ |
|
|||
|
|
|
|
|
|
|
|
|
|
||||
Условное обозначение |
; |
|
|
|
|||||||||
; zy ( x, y ); |
f y ( x, y ). |
|
|||||||||||
|
|
|
|
|
∂y |
∂y |
|
|
|
|
|
|
|
Пример. |
z = x2 + y2 + xy |
∂z = 2x + y , |
∂z |
= 2 y + x. |
|||||||||
|
|||||||||||||
|
|
|
|
|
|
|
∂x |
|
|
|
∂y |
|
|
Аналогично можно рассматривать функции большего числа переменных.
2.4.3. Частные производные высших порядков
Частные производные |
∂z и |
∂z функции двух переменных z = f ( x, y ) |
|
∂x |
∂y |
также являются функциями двух переменных и их можно продифференцировать по x и по y. Тогда получаются 4 производных второго порядка.
∂ |
∂z |
= |
∂2 z |
||
|
|
|
|
∂x2 |
|
|
|||||
∂x |
∂x |
|
|||
¶ |
¶z = ¶ z |
||||
|
|
|
|
|
2 |
|
|
|
|
|
|
¶y |
¶y |
|
¶y2 |
||
Производные
= z′′
xx
= z¢¢
yy
∂2 z
∂x∂y
|
∂ |
∂z |
= |
|
∂2 z |
= z′′ . |
|||
|
|
|
|
|
|
|
|||
|
|
|
|
∂y∂x |
yx |
||||
∂y |
∂x |
|
|
||||||
|
¶ |
¶z |
= |
|
¶2 z |
= z¢¢ . |
|||
|
|
|
|
|
|
||||
|
|
|
|
|
¶x¶y |
xy |
|||
|
¶x |
¶y |
|
|
|
||||
∂2 z
и∂y∂z называются смешанными.
Теорема. Если смешанные производные второго порядка непрерывны, то
они равны. |
|
|
|
|
|
|
|
|
|
Пример. |
|
|
|
|
|
|
|
|
|
z = exy ; |
∂z = yexy ; |
∂z |
= xexy ; |
|
|
||||
|
|
|
|||||||
|
∂x |
|
|
∂y |
|
|
|
|
|
¶2 z = y2exy ; |
¶2 z |
= x2 × exy ; |
∂2 z |
= exy + xyexy ; |
∂2 z |
= exy + xyexy . |
|||
¶y2 |
|
|
|||||||
¶x2 |
|
|
|
|
∂x∂y |
∂y∂x |
|||
|
|
|
|
|
|
39 |
|
|
|
Далее дифференцируя производные второго порядка получаются производные третьего порядка и т.д.
Разных производных n -го порядка будет (n + 1).
2.4.4. Производная функции по направлению
Рассмотрим функцию трех переменных u ( x, y, z ) . Возьмем в пространстве точку M и исходящий из нее луч ℓ. На луче ℓ выберем точку M1 . Обозначим
MM1 = ℓ.
ℓ
M1
ℓ
M
РИС. 2.4.2
Определение: Производной по направлению ℓ от функции
u = u ( x, y, z ) называется предел |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
∂u |
= lim |
u (M1 ) − u (M ) |
. |
|
|
|
|
|
|||
|
|
|
|
∂ℓ |
|
|
|
|
|
||||||
|
|
|
|
ℓ→0 |
|
ℓ |
|
|
∂u |
|
|
|
|
||
Обозначение производной по направлению |
. |
|
|
|
|||||||||||
∂ℓ |
|
|
|
||||||||||||
Производная |
∂u |
|
- это скорость изменения функции u в точке M по |
||||||||||||
∂ℓ |
|||||||||||||||
направлению l . |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Если направление ℓ совпадает с положительным направлением коорди- |
|||||||||||||||
|
∂u |
|
|
|
|
|
|
|
|
|
∂u |
|
|
||
натной оси |
Ox , то ∂ℓ |
совпадают с частной производной |
∂x |
и т.п. |
|
||||||||||
Пусть |
направление |
ℓ характеризуется направляющими |
косинусами |
||||||||||||
cos α, cosβ, |
cos γ . Тогда можно показать, что |
|
|
|
|
|
|
|
|||||||
|
|
∂ u = ∂ u cos α + |
∂ u |
cosβ + |
∂ u cos γ . |
|
|
(5) |
|||||||
|
|
|
|
|
|||||||||||
|
|
∂ l |
∂ x |
|
|
∂ y |
∂ l |
|
|
|
|||||
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
|
|
