
МатАн_ЛинАлг_080100 / Лекции_Математика_2_Дифференциальное исчисление
.pdf
1.3.3. Функция непрерывная на интервале
Функция называется непрерывной на интервале, если она непрерывна в каждой точке этого интервала.
Тема 2. Дифференциальное исчисление
2.1. Основы дифференциального исчисления
Производная – основное понятие высшей математики, характеризующее скорость изменения функции. Раздел математики, в котором изучаются производные и их применение к исследованию функций, называется дифференциальным исчислением. Основные положения его были сформулированы И. Ньютоном и Г. Лейбницем. С открытием дифференциального исчисления сильно расширилась область применения математики, началась новая эпоха ее развития.
Исторически понятие производной возникло из задач естествознания и математики, приводящих к вычислению пределов одного и того же вида – скорость прямолинейного движения точки и построение касательной к кривой.
Основные понятия дифференциального исчисления изучаются в средней школе, и это будет учитываться при изложении материала. Дифференциальное исчисление излагается в училище в большом объеме на более высоком уровне.
2.2.Учебные вопросы лекции:
2.2.1.Определение производной
2.2.1.1.Определение и вычисление производной.
Рассмотрим функцию y = f (x) . Фиксируем значение x.
Производной функции y = f (x) в точке x называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Обозначение производной: y′, y′ , f ′(x), dy .
x
dx
Таким образом:
21

y′ = lim y
x→0 x
Замечание. Производная в фиксированной точке – это число, если x D( y) – переменная величина, то производная y′ – это функция от x .
Операция отыскания производной называется дифференцированием
функции.
Пример. y = x2 . Найти y′
Решение.
1)f (x + x) = (x + x)2 = x2 + 2x × x + ( x)2 ,
2)y = x2 + 2x × x + ( x)2 - x2 = 2x × x + ( x)2 ,
3)y = 2x + x,
x
4)y′ = lim (2x + x) = 2x.
x→0
Итак, y = x2 y¢ = 2x.
Значение производной в фиксированной точке x0 обозначается:
y′ |
|
f ′(x0 ), |
dy |
x = x0 |
||
x |
|
|
||||
dx |
||||||
|
= x0 , |
|||||
2.2.1.2. Механический смысл производной. |
||||||
Рассмотрим функцию s = s (t) , где s |
– путь пройденный телом, t – время. |
|||||
Тогда s′(t) = v – скорость движения.
2.2.1.3. Геометрический смысл производной
|
T |
N |
y = f ( x) |
|
|
|
|
M 0 |
α |
β |
y |
|
|
|
|
22

Пусть |
линии |
– |
график |
функции |
y = f (x) , |
а |
точки |
||||
M 0 (x0 , y0 ), N (x0 + x, y0 + y) лежат на линии. |
|
|
|
||||||||
Пусть: β - угол наклона секущей M 0 N к оси Ox; |
α - угол наклона каса- |
||||||||||
тельной к оси Ox. |
|
|
|
|
|
|
|
|
|||
Тогда tgβ = |
y |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
Если N → M0, то x → 0, |
β → α . Следовательно, |
|
|
|
|||||||
|
|
|
|
tgα = lim tgβ = lim |
y |
. |
|
|
|
||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
β→α |
x→0 |
x |
|
|
|
|
Так как tgα называется угловым коэффициентом касательной, то получа-
ем геометрический смысл производной функции y = f (x) в точке x0 :
f ′(x0 ) = kкас – угловой коэффициент касательной к графику функции в точке M 0 .
Используя уравнение прямой, проходящей через точку M 0 (x0 , y0 ) с угло-
вым коэффициентом
y - y0 = k (x - x0 )
получим уравнение касательной
y − y0 = f ′(x0 )(x − x0 ) .
2.2.2.Правила дифференцирования. Таблица производных
2.2.2.1.Производная суммы, произведения и частного
Из школьного курса математики известны следующие формулы
1)C′ = 0, где C - постоянная;
2)(u + v)′ = u′ ± v′
3)(u × v)′ = u′v + uv′
4)u ′ = u′v − uv′v v2
где u = u(x), v = v(x) – дифференцируемые функции.
Все формулы выводятся по шагам.
23

Следствия.
1)(cu )¢ = cu¢,
2)(u × v × w)¢ = u¢ × v × w + u × v¢ × w + u × v × w¢,
3)u ¢ = 1 × u¢ = u¢.c c c
2.2.2.2. Производные основных элементарных функций: тригонометриче-
ских, логарифмической.
а) Производные тригонометрических функций Теорема. Формулы производных четырех тригонометрических функций
имеют вид:
|
|
|
|
1) y = sin x, |
y′ = cos x; |
|
|
2) y = cos x, |
y′ = −sin x; |
|||||||||||||||||||
|
|
|
|
3) y = tgx, |
y¢ = |
|
1 |
|
; |
4) y = ctgx, |
y¢ = - |
1 |
. |
|||||||||||||||
|
|
|
|
cos2 x |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin2 |
x |
|||||||
б) Производная логарифмической функции |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Найдем производную функции y = loga x : |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1. y = loga ( x + x) - loga x = loga |
|
x + x |
|
|
|
|
x |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
= loga |
1 + |
|
; |
|
|
|
|
|
|
|||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|||
|
y |
|
1 |
|
x |
|
1 |
|
|
x |
|
|
|
|
|
x |
1 |
|
|
|
x |
x |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|||||||||||||||||
2. |
|
= |
|
loga 1 + |
|
|
= |
|
|
× |
|
loga 1 |
+ |
|
|
= |
|
loga 1 + |
|
|
|
; |
||||||
x |
x |
|
x |
x |
|
x |
|
|
||||||||||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
x |
|
|
x |
|
|
|
||||||||||
3.y¢ = lim y =
x→0 x
Частный случай
1 |
|
|
|
|
|
x |
|
x |
|
|
1 |
|
|
|
|
|
|
+ |
x |
= |
|
|
|
||||||
|
lim loga 1 |
|
|
|
|
|
loga |
lim |
||||||
|
x |
|
|
|||||||||||
x x→0 |
|
|
|
|
|
|
|
|
x |
x→0 |
||||
|
|
= |
1 |
loga e = |
|
|
1 |
. |
|
|
||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
x |
|
|
|
x ln a |
|
|
|
||||
(a = e, ln e =1) :
y = ln x, y¢ = 1 x
|
|
x |
x |
|
|
+ |
x |
= |
|||
1 |
|
|
|
||
|
|
||||
|
|
x |
|
|
|
24
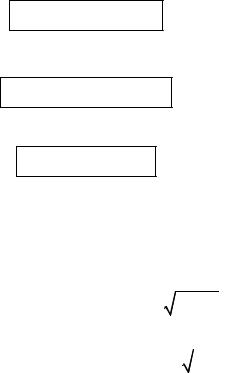
2.2.2.3. Производная степенной и показательной функций.
а) Степенная функция y = xn
y = xn y′ = nxn−1
б) Показательная функция y = a x .
y = a x y′ = ax ln a
Частный случай
y = ex y′ = ex
2.2.2.4. Производные обратных тригонометрических функций.
Производные этих функций имеют вид:
1) y = arcsin x, |
y′ = |
|
|
1 |
|
|
; |
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 − x2 |
||||||||||
2) y = arccos x, |
y′ = − |
|
|
1 |
|
|
|
|
; |
||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
1 − x2 |
|||||||
3) y = arctgx, y′ = |
1 |
|
; |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||||
1 + x2 |
|
|
|
|
|
||||||||
4) y = arcctgx, |
y′ = − |
1 |
|
|
. |
||||||||
|
|||||||||||||
1 + x2 |
|||||||||||||
2.2.3. Производная сложной функции.
Определение:
Функция y называется сложной функцией переменной x , если
y = f (u ), u = g ( x) y = f g ( x) ,
а u называется промежуточной переменной. Примеры:
1)y = u2 , u = tg x y = tg2 x;
2)y = ln u, u = sin x y = ln sin x.
Функции y = f (u ), u = g ( x) называются звеньями сложной функции. Го-
ворят, что сложная функция состоит из двух звеньев. Сложная функция может состоять из большего числа звеньев. Например, функция
25
y = f g (j( x)) состоит из трех звеньев.
Например:
y = u2 , u = cos v, v = ln x y = cos2 (ln x)
При дифференцировании сложной функции важно уметь представить ее в виде цепочки звеньев.
Например. y = ctg ln x2 y = ctg u, |
u = ln v, v = x2 . |
||||||||||
Теорема. |
|
|
|
|
|
|
|
|
|
|
|
Если функции y = f (u ), |
u = g ( x) |
|
дифференцируемы, то производная |
||||||||
сложной функции y = f g ( x) |
находится по формуле |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
y¢ |
= y¢ × u¢ |
|
||
|
|
|
|
|
|
|
|
x |
u |
x |
|
(правило цепочки). |
|
|
|
|
|
|
|
||||
Доказательство: |
|
|
|
|
|
|
|
||||
Примеры: |
) |
|
|
|
|
|
|
|
|
||
1) y = sin |
( |
x2 |
|
|
|
|
|
|
u |
x |
|
|
|
y = sin u, u = x2 y¢ |
= cosu, u¢ = 2x, |
||||||||
x |
|
|
|
x |
( |
x2 |
) |
× 2x. |
|
|
|
y¢ = cosu |
× 2x y¢ = cos |
|
|
|
|
||||||
При решении задач промежуточные переменные стараются не вводить.
2) y = tg (2x + 1) y¢ |
1 |
× ( |
2x + 1)¢ = |
|
2 |
|
|
|
|
|
= |
|
|
. |
|
||||||
cos2 (2x + 1) |
cos2 (2x + 1) |
|
||||||||
Замечание. Если y = f (u ), u = g (v), |
v = j( x), то |
′ |
′ |
|
′ |
′ |
||||
yx |
= yu |
× uv |
× vx . |
|||||||
2.2.4.Производные неявных функций
2.2.4.1.Неявные функции одной и двух переменных
Пусть значения двух переменных x и y связаны между собой уравнени-
ем
F ( x, y) = 0 . |
(4) |
Такой способ задания зависимости между x и y называется неявной функци-
ей
26
Интересно было бы получить формулы дифференцирования неявной функции, которые можно было бы применять, не выражая y из уравнения.
Пусть уравнение F ( x, y ) = 0 определяет неявную функцию y = y ( x) . Для отыскания производной y′(x) можно поступить следующим образом:
1)Найдем производную функции F ( x, y ) , помня, что y = y ( x) .
2)Из полученного равенства найдем выражение производной y′(x) .
Пример 5.
Найти производную неявной функции x2 + y2 = 4 в точке M (
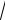 2,
2, 
 2 ) .
2 ) .
Решение. Чтобы найти функцию F ( x, y ) перенесем число 4 в левую
часть уравнения. Тогда x2 + y2 − 4 = 0.
Найдем производные обеих частей равенства
2x + 2 y × y′ = 0 .
Отсюда найдем
y′ = − x .
|
|
|
|
|
y |
Следовательно, |
|
|
|
|
|
y′ |
|
x= |
|
= −1. |
|
|
2 |
||||
|
|
|
y= |
2 |
|
2.2.5. Производные высших порядков |
|||||
Производная y′ функции |
y = f (x) называется производной первого по- |
||||
рядка или первой производной. |
Она является функцией от x , а значит, тоже |
||||
имеет производную. |
|
|
|
|
|
Производная от первой производной ( y′)′ называется производной вто-
рого порядка (второй производной) и обозначается
2
y′′, f ′′(x), d y , d x2
то есть y′′ = ( y′)′ .
27

Аналогично, производная третьего порядка y′′′ = ( y′′)′ обозначается так-
3
же f ′′′(x), d y . d x3
В общем случае, производная n -го порядка – это производная от производной (n − 1) -го порядка
y(n) = ( y(n−1) )′ .
Механический смысл второй производной. Если функция s = s (t) –
уравнение прямолинейного движения точки, а s′(t) = v(t) – скорость движения,
то s′′(t) – это скорость изменения скорости, то есть ускорение a (t) . Таким об-
|
′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
разом, s (t) = a (t) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Пример. y = ln (1 + sin t) , |
|
y′′ = ? |
|
|
|
|
|
|
|
|
|
|
||||||
|
Решение. y′ = |
|
cost |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
+ sin t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y′′ = -sin t × (1 + sin t) - cost × cost = |
|
-sin t -1 |
= |
|
-1 |
. |
|
|
||||||||||
|
(1 + sin t)2 |
|
|||||||||||||||||
|
|
|
(1 + sin t)2 |
|
|
|
1 + sin t |
||||||||||||
|
2.2.6. Правило Лопиталя |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Теорема. Пусть функции f (x) |
и g(x) |
|
определены и непрерывны в неко- |
|||||||||||||||
торой окрестности точки x0 , причем |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
lim |
f (x) = lim g(x) = 0 |
|
|
|
|
|
|
|||||||||
|
′ |
x→x0 |
|
|
|
x→x0 |
|
|
|
|
|
|
|
|
|
|
|||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
g (x) ¹ 0 в данной окрестности. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Тогда, если существует предел отношения производных lim |
f ′(x) |
, то |
||||||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→x0 g′(x) |
||
существует предел отношения функций lim |
|
f (x) |
и эти пределы равны |
||||||||||||||||
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
x→x0 g(x) |
|
|
|
|
|
|
|||||
|
|
|
lim |
|
f (x) |
= lim |
f ′(x) |
. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
x→x0 g(x) |
x→x0 g′(x) |
|
|
|
|
|
|
|||||||||
Замечания:
28

1. В формулировке теоремы условие x → x0 можно заменить на условие
x→ ∞ .
2.Правило Лопиталя можно применить несколько раз.
3.Утверждение теоремы остается справедливым, если в условии выполняется равенство
|
|
|
|
|
|
lim |
f (x) = lim g(x) = ∞ . |
|
|
|
|
|
|
x→x0 |
x→x0 |
|
|
|
|
Таким образом, правило Лопиталя позволяет раскрыть неопределенности |
|||
|
0 |
|
, |
|
¥ |
. С помощью правила Лопиталя можно раскрыть неопределенности |
|
|
|
|
|
|
|||
|
|||||||
|
0 |
|
|
|
¥ |
|
|
|
0 |
|
¥ |
||
(0 × ¥), (¥ - ¥) , если их предварительно преобразовать к виду |
|
|
или |
¥ |
. |
|
|||||
|
0 |
|
|
||
|
ex -1 |
|
0 |
Л |
(ex -1)′ |
|
ex |
2 |
||
lim |
|
|
= |
|
|
= lim |
( x)¢ |
= lim |
|
=1. |
|
|
|
||||||||
x→0 x |
|
0 |
x→0 |
x→0 1 |
|
|||||
2.3. Приложение производной для исследования функций
При решении многих задач техники и экономики возникает проблема выбора оптимального варианта среди множества возможных решений. Например, требуется найти решение экономической задачи, обеспечивающее наибольшую прибыль или наименьшие издержки производства. В первом случае нам нужно найти точку, в которой достигается наибольшее значение функции прибыли, во втором – наименьшее значение функции издержек. Простейшие задачи оптимизации сводятся к задачам исследования функции одной переменной на экстремум. Поэтому данная тема имеет важное прикладное значение.
На данной лекции мы познакомимся с понятиями возрастающей и убывающей функций, точки максимума и точки минимума, рассмотрим методы исследования на возрастание, убывание и точки экстремума.
Л
2 Знак = означает использование правила Лопиталя.
29
2.3.1. Условия возрастания и убывания функции
Определения.
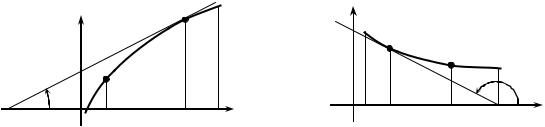
1)Функция y = f (x) называется возрастающей на интервале (a,b) , если большему значению аргумента x2 > x1 , x1, x2 (a,b) соответствует большее значение функции f (x2 ) > f (x1 ) (Рис. 2.3.1).
2)Функция y = f (x) называется убывающей на интервале (a,b) , если большему значению аргумента x2 > x1 , x1, x2 (a,b) соответствует меньшее значение функции (Рис. 2.3.2).
y |
|
|
|
|
|
|
|
|
|
f(x2) |
|
α |
f(x1) |
||
O a x1 |
|
x2 b x |
|
x1 < x2 f (x1 ) < f (x2 )
РИС. 2.3.1
y |
|
|
|
||
|
|
|
|
|
|
|
f(x1) |
|
f(x2) |
|
α |
|
|
|
|
||
O a x1 |
x2 |
b |
x |
||
x1 < x2 f (x2 ) < f (x1 )
РИС. 2.3.2
Теорема 1. (Достаточное условие возрастания)
Если |
′ |
при x (a,b) , то функция f (x) |
возрастает на интервале |
f (x) > 0 |
|||
(a,b) . |
|
|
|
Доказательство. |
Пусть x1, x2 - произвольные точки из интервала (a,b) и |
||
x1 < x2 . Запишем формулу Лагранжа для функции f (x) |
на отрезке [x1, x2 ] |
||
f (x2 ) - f (x1 ) = |
′ |
|
|
f (x0 ) × (x2 - x1 ) , x0 Î(x1, x2 ) . |
|||
′ |
при любых |
′ |
> 0 , так как x0 Î(x1, x2 ) , |
Так как f (x) > 0 |
x (a,b) , то f (x0 ) |
||
а значит x0 Î(a, b) . По выбору x1 < x2 , следовательно x2 - x1 > 0 . Таким обра-
зом,
f ′(x0 ) × (x2 - x1 ) > 0 f (x2 ) - f (x1 ) > 0 f (x2 ) > f (x1 ) ,
то есть, согласно определению 1), функция f (x) возрастает.
Теорема 2. (Достаточное условие убывания).
30
