
МатАн_ЛинАлг_080100 / Лекции_Математика_2_Дифференциальное исчисление
.pdf1.1.3.7. Эквивалентность высказываний |
|
|
|
|
|
Таблица истин- |
|||
Эквивалентностью высказываний A и B называется |
|
|||
высказывание A B (« A тогда и только тогда, когда B |
|
|
ности |
|
»), которое истинно, если A и B оба истинны или оба лож- |
|
|
|
|
|
A |
B |
A B |
|
ны. |
|
|
|
|
1 |
1 |
1 |
||
Эквивалентность A B соответствует логической |
|
|
|
|
1 |
0 |
0 |
||
связке A «… тогда и только тогда, когда … ». |
|
|
|
|
0 |
1 |
0 |
||
|
|
|
|
|
|
|
0 |
0 |
1 |
|
|
|
|
|
1.1.4. Кванторные операции
Для предикатов можно ввести операции, не имеющие аналогов среди операций над высказываниями. Это – кванторные операции. Применение этих операций превращает предикат в высказывание.
Выражение «для любого x » (для всякого x , для каждого x ) называется
квантором общности по переменной x и обозначается x (английское слово
ALL – все).
« "x : Ф ( x) » – для любого x верно Ф( x) .
Выражение «существует x » (есть x , найдется x ) называется квантором существования по переменной x и обозначается x (английское слово Existence – существование).
Примеры:
1)« x : sin2 x + cos2 x = 1» – истинно.
2)« x : x2 − 4 = 0 » – истинно.
При использовании кванторов часто указывается множество, из которого берется переменная x .
Например:
1)« x : x + 10 = 2 » – ложно.
2)« x : x + 10 = 2 » – истинно.
1.1.5. Кванторы общности, существования и единственности
В математике часто используется символическая форма записи. Ранее
уже были введены такие символы, как , , , , \ , , , ∩, : , ¾¾f ®.
11
Кроме них при записи определений и формулировок теорем будут также использоваться и другие символы, в частности, символы логических операций (
; ; , ).
Также в математике используются операции, которые называются кван-
торными1 операциями.
Квантором общности по переменной x называется выражение «для любого x » (для всякого x , для каждого x ) и обозначается "x (английское сло-
во All – все).
« x : G ( x) » – для любого x верно G ( x) .
Квантором существования по переменной x называется выражение
«существует x » («есть x », «найдется x ») и обозначается $x (английское слово Existence – существование).
Из других кванторов можно указать квантор единственности, обознача-
емый !x |
(«для одного и только одного |
x »). Обычно квантор единственности |
|||||||||||
используется совместно с квантором существования: $!x . |
|
|
|
||||||||||
|
Примеры: |
|
|
|
|
|
|
||||||
1. |
|
« "x : sin 2x = 2sin x × cos x » – |
для |
любого x |
верно |
равенство |
|||||||
sin 2x = 2sin x × cos x ; |
|
|
|
|
|
|
|||||||
|
|
|
« x : |
|
|
= 5 » |
|
|
|
|
|||
2. |
|
x2 − 9 |
– существует x , |
для которого |
верно |
равенство |
|||||||
|
|
= 5; |
|
|
|
|
|
|
|
|
|||
|
x2 − 9 |
|
|
|
|
|
|
||||||
3. |
|
« !x : |
x − 3 |
= 0 » – |
для одного и только для одного |
x |
верно равенство |
||||||
|
|
||||||||||||
|
|
|
|
x + 3 |
|
|
|
|
|
|
|||
x − 3 =
x + 3
0 .
1 Термин «квантор» ввёл Ч. Пирс в 1885 г.
12
1.2.Теория пределов
1.2.1.Числовые последовательности
1.2.1.1.Числовые последовательности
Числовой последовательностью называется функция, определенная на множестве натуральных чисел.
Обозначение: yn = f (n), n = 1, 2,3,...
Определенная таким образом функция каждому натуральному числу n ставит в соответствие действительное число yn . Числовая последовательность записывается в виде y1, y2 , y3 , ..., yn , ... или кратко { yn } .
Числа y1, y2 , ... yn , называются членами последовательности, yn - об-
щим или |
|
n -м |
членом. |
Каждый член |
последовательности характеризуется |
||||||||||||||||
натуральным числом – |
своим номером в последовательности. |
||||||||||||||||||||
Примеры. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1) |
y |
|
= |
|
1 |
|
или |
y |
|
: |
1 |
; |
1 |
; |
1 |
; ... |
|
1 |
|
; ... |
|
|
|
n + 1 |
|
|
|
|
|
|
|
||||||||||||
|
|
n |
|
|
|
|
|
n |
|
2 3 4 n + 1 |
|
||||||||||
2) |
yn = (−1)n + 1 |
или |
|
|
yn : 0; 2; 0; 2,... |
|
|||||||||||||||
3) |
yn = n2 |
или |
|
yn :1, 4, 9, ... |
|
|
|
||||||||||||||
4) |
y1 = a1, |
yn = yn−1 + d - арифметическая прогрессия. |
|||||||||||||||||||
Числовая последовательность может быть определена формулой общего |
|||||||||||||||||||||
члена yn (примеры 1, |
2, |
3), а может быть задана с помощью рекуррентной |
|||||||||||||||||||
формулы (пример 4). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1.2.1.2. Ограниченные и неограниченные последовательности
Последовательность { yn } называется ограниченной сверху (снизу), если существует число M (число m ) такое, что каждый элемент этой последовательности yn удовлетворяет неравенству
yn £ M ( yn ³ m ). |
(1) |
13 |
|

При этом число M (число m ) называется верхней гранью (нижней гра-
нью) последовательности { yn } .
Последовательность { yn } называется ограниченной с обеих сторон (или просто ограниченной), если она ограничена и сверху, и снизу, т.е. если существуют два вещественных числа M и m такие, что каждый элемент этой по-
следовательности yn удовлетворяет неравенствам |
|
|||||
m ≤ yn ≤ M . |
(2) |
|||||
Последовательность { yn } называется неограниченной, если для любого |
||||||
положительного числа A найдется хотя бы один элемент последовательности |
||||||
yn , удовлетворяющий неравенству |
|
|||||
|
yn |
|
> A . |
(3) |
||
|
|
|||||
Пример 1. Последовательность |
|
|
{ |
1 |
}, очевидно, |
является ограниченной: |
|
|
|
||||
|
|
|
|
n |
|
|
каждый элемент этой последовательности удовлетворяет неравенствам
0 < 1 ≤ 1. n
1.2.1.3. Бесконечно большие последовательности. Бесконечно малые по-
следовательности и их свойства.
1.2.1.4. Бесконечно большие и бесконечно малые последовательности
Введем теперь понятия бесконечно большой и бесконечно малой последовательностей.
Последовательность { yn } называется бесконечно большой, если для лю-
бого положительного числа A найдется номер N такой, что при всех n ³ N элементы yn этой последовательности удовлетворяют неравенству (3).
Последовательность {αn } называется бесконечно малой, если для любо-
го положительного числа ε найдется номер N такой, что при всех n ³ N элементы αn , этой последовательности удовлетворяют неравенству
αn ≤ ε .
14
1.2.2. Предел последовательности
Последовательность { yn } называется сходящейся, если существует такое вещественное число a , что последовательность { yn − a} является бесконечно малой.
При этом вещественное число a называется пределом последовательно-
сти { yn } .
Символически это записывают так:
lim yn = a или yn → a при n → ∞ .
n→∞
Замечание 1. Последовательности, не являющиеся сходящимися, принято называть расходящимися.
Замечание 2. Иногда формально договариваются трактовать бесконечно большие последовательности как последовательности, сходящиеся к пределу ∞
:
lim yn = ∞ .
n→∞
1.2.2.1. Свойства сходящихся последовательностей
Перейдем к свойствам произвольных сходящихся последовательностей.
Теорема 1. Сходящаяся последовательность имеет только один пре-
дел.
Теорема 2. Всякая сходящаяся последовательность является ограниченной.
Замечание 4. Не всякая ограниченная последовательность является сходящейся. Так, например, последовательность 0, 1, 0, 1, ..., 0, 1, ... является ограниченной, но не является сходящейся.
Теорема 3. |
Сумма сходящихся последовательностей |
{ xn } и |
{ yn } |
представляет собой |
сходящуюся последовательность, предел |
которой |
равен |
сумме пределов последовательностей { xn } и { yn } .
Аналогично можно сказать и про разность, произведение и частное сходящихся последовательностей. При этом предел последовательности, стоящей в знаменателе не должен равняться нулю.
15
1.2.3. Предел функции в точке. Бесконечно малые и бесконечно большие функции
1.2.3.1. Проколотая окрестность
Перейдем к изучению свойств функции вблизи некоторой точки.
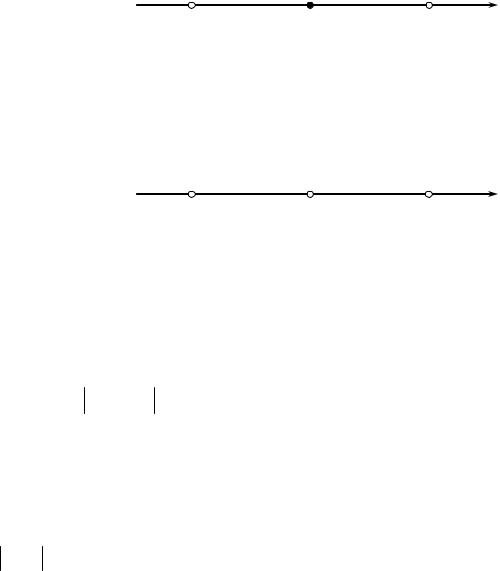
Вспомним, что окрестностью U r |
точки a называется интервал |
a |
|
(a − r, a + r ) , r − радиус окрестности. |
|
a − r |
a |
a + r |
x |
РИС. 1.2.1
Определение 1.1.1. Проколотой окрестностью Uɺar точки a называется ее окрестность, из которой удалена сама точка a .
a − r |
a |
a + r |
x |
|
РИС. 1.2.2 |
|
|
1.2.3.2. Предел функции в точке. Бесконечно малая функция
Число b является пределом функции f ( x) при x → a, если для любого
ε > 0 существует проколотая окрестность точки a , в которой выполняется неравенство f ( x) − b < ε.
Обозначение lim f ( x) = b .
x→a
Функция α ( x ) называется бесконечно малой функцией (б.м.ф.) при
x → a , если для любого ε > 0 в окрестности точки a выполняется неравенство
α ( x) < ε .
Тогда определение предела функции f ( x) при x → a можно записать та-
ким образом
lim f ( x) = b f ( x) = b + α( x), где α ( x ) – б.м.ф. при x → a .
x→a
16

Замечание. Теорема о единственности предела, которую мы рассматривали для последовательностей, справедлива и для функций.
1.2.3.3. Бесконечно большие функции
Функция f ( x) называется бесконечно большой функцией (б.б.ф.) при
x ® a ( x ® ± ¥) , |
если функция |
|
1 |
|
бесконечно малая при x ® a ( x ® ± ¥), |
||||
|
f ( x) |
|
|||||||
1 |
|
|
1 |
|
|
|
|||
то есть lim |
|
|
= 0 |
lim |
|
= 0 . |
|
||
|
|
|
|||||||
x→a f ( x) |
x→±∞ f ( x) |
|
|
||||||
Обозначения: lim f ( x) = ± ¥( lim |
f ( x) = ± ¥). |
||||||||
|
|
|
x→a |
|
|
|
x→±∞ |
||
В символической форме определение и свойства б.б.ф. можно записать
так:
1)¥1 = 0 ;
2)1 = ¥ ;
0
3)¥ × ¥ = ¥ ;
4) |
¥ × A = ¥, A - число; |
5) |
∞ + ∞ = ∞, если б.б.ф. имеет одинаковые знаки. |
1.2.4.Основные теоремы о пределах
1.2.4.1.Теоремы о пределах
Пусть lim f ( x) = b, |
lim g ( x) = c . Тогда справедливы следующие теоре- |
x→a |
x→a |
мы. |
|
Теорема 4. |
Предел суммы двух функций равен сумме их пределов, т.е. |
||
lim ( f ( x) + g ( x)) = lim f ( x) + lim g ( x) = b + c. |
|||
x→a |
x→a |
x→a |
|
Теорема 5. |
Предел произведений двух функций равен произведению их |
||
пределов, то есть |
|
|
|
|
lim f ( x) × g ( x) = lim f ( x) × lim g ( x) = b × c |
||
|
x→a |
x→a |
x→a |
|
|
|
17 |

Теорема 6. Предел частного двух функций равен частному их пределов, если предел знаменателя не равен нулю, то есть
|
f ( x) |
|
lim f ( x) |
|
b |
|
lim g ( x) = c ¹ 0 |
lim |
= |
x→a |
= |
, |
|||
|
lim g ( x) |
|
|||||
x→a g ( x) |
|
|
c |
x→a |
|||
|
|
|
x→a |
|
|
|
|
Следствия.
1) Предел постоянный равен самой постоянной
lim C = C, C = const .
x→a
2) Постоянный множитель можно вынести за знак предела
lim C × f ( x) = C × lim f ( x). |
|
x→a |
x→a |
Замечание. Рассмотренные теоремы справедливы для случаев x → ± ∞.
Пример 2. Вычислить предел lim 2x2 + 5 .
x→2 x2 − 3
Решение:
При решении данного примера воспользуемся теоремами о пределах.
|
2x |
2 |
+ 5 |
|
|
|
lim (2x2 + 5) |
|
2lim( x2 ) + lim 5 |
|
2 × 4 + 5 |
|
|||
lim |
|
= |
x→2 |
|
= |
x→2 |
x→2 |
= |
=13. |
||||||
|
|
|
|
|
( x2 - 3) |
|
( x2 ) - lim 3 |
|
|||||||
x→2 x2 - 3 |
|
|
|
lim |
|
lim |
4 - 3 |
|
|||||||
|
|
|
|
|
|
|
x→2 |
|
|
x→2 |
x→2 |
|
|
|
|
Таким образом, искомое значение предела находится путем подстановки |
|||||||||||||||
x = 2 в выражение |
|
x2 |
+ 5 |
|
. |
|
|
|
|
|
|
||||
|
x2 |
− 3 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
1.2.5.Неопределенности
1.2.5.1.Неопределенности
Теоремы о пределах позволяют осуществлять переход к пределу в арифметических действиях. Однако существуют случаи, когда невозможно предсказать поведение результата арифметических действий. Такие случаи называются неопределенностями. Приведем некоторые виды неопределенностей, используя символическую форму записи.
1)0 - отношение двух б.м.ф.0
18

2)¥ - отношение двух б.б.ф.¥
3)(0 × ¥) - произведение б.м.ф. на б.б.ф.
4)(¥ - ¥) - разность двух б.б.ф. одного знака.
Отыскание предела в этих случаях называется раскрытием неопреде-
ленности.
1.2.5.2. Раскрытие неопределенностей
Рассмотрим раскрытие неопределенностей на конкретных примерах.
Пример 3. Вычислить предел lim x2 -1 .
x→1 x -1
Решение:
Если подставить в выражение функции значение x = 1, то получим, что и числитель и знаменатель дроби обращаются в нуль. Следовательно, имеем не-
|
0 |
|
: |
|
|
|
|
|
|
определенность типа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
− 1 |
|
0 |
|
|
|
|
|
lim |
|
|
|
= |
|
. |
|
|
|
|
− 1 |
0 |
||||
|
|
|
x→1 x |
|
|
||||
Для раскрытия неопределенности следует выделить в числителе и в зна- |
|||||||||
менателе «критический множитель» (то есть множитель, обращающий их в нуль при x = 1) и сократить его.
|
x2 |
− 1 |
|
0 |
|
( x − 1) ( x + 1) |
= lim( x + 1) = 2. |
||
lim |
|
|
|
= |
|
|
= lim |
|
|
|
− 1 |
|
x − 1 |
||||||
x→1 x |
|
0 |
x→1 |
x→1 |
|||||
Пример 4. Вычислить предел lim 2x2 − 1 .
x→∞ x3 + x
Решение:
Видно, что при x → ∞ числитель и знаменатель дроби стремятся к беско-
нечности. Следовательно, имеем неопределенность типа ¥ :¥
|
2x2 |
− 1 |
|
∞ |
||
lim |
|
|
|
|
= |
. |
|
+ x |
|||||
x→∞ x3 |
|
∞ |
||||
19

Для раскрытия такой неопределенности следует вынести из числителя и знаменателя переменную x в старших степенях и, проведя затем сокращения, вычислить предел.
|
|
|
|
|
|
|
|
|
2 |
|
2x2 |
|
− |
1 |
|
|
|
|
2 − |
1 |
|
|
|
|
|
|
|||||||||||
|
|
2 |
− 1 |
|
∞ |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2x |
|
|
|
|
2 |
|
|
|
|
2 |
|
2 |
|
|
2 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
||||||||
lim |
|
|
|
|
= |
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
= |
|
= 0. |
|||||||||
|
+ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
∞ |
||||||||||||||
x→∞ x3 |
|
∞ |
x→∞ |
|
|
|
x |
2 |
|
+ |
x |
|
|
x→∞ |
+ |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
|
|
x |
1 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1.2.5.3. Замечательные пределы
Также как и в случае предела числовой последовательности, для предела функции справедливы замечательные пределы.
Первый замечательный предел в данном случае записывается в виде:
lim sin x = 1,
x→0 x
а второй замечательный предел –
|
|
1 x |
||
lim 1 |
+ |
|
|
= e |
|
||||
x→∞ |
|
x |
|
|
или
1
lim (1 + x) x = e .
x→0
1.3.Непрерывность функции
1.3.1.Первое определение непрерывности
Функция y = f ( x) , определенная в некоторой окрестности точки x0 ,
называется непрерывной в точке x0 , если выполняется равенство:
lim f ( x) = f ( x0 ) .
x→x0
1.3.2. Второе определение непрерывности
Функция y = f ( x) называется непрерывной в точке x0 , если бесконечно малому приращению аргумента x в точке x0 соответствует бесконечно малое приращение функции y .
20
