
080100Экономика(МатАнализ и ЛинАлгебра) / Лекции_Линейная_алгебра
.pdf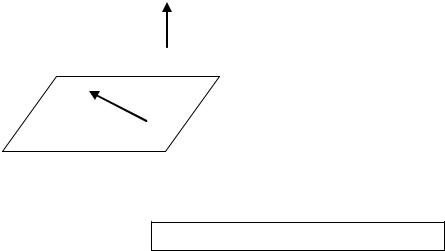
3.2. Плоскость и прямая в пространстве. Основные задачи аналитической геометрии
3.2.1.Уравнения плоскости и прямой в пространстве
3.2.1.1.Уравнение плоскости
Рассмотрим прямоугольную декартову систему координат в пространстве.
Каждая точка в этой системе имеет три координаты |
|
|
|
|
|||
Рассмотрим плоскость в пространстве |
3 . Получим различные виды ее |
||||||
уравнения и отметим их основное свойство. |
|
|
|
|
|
||
1. Вектор N =(A, B, C ), перпендикулярный плоскости, называется нор- |
|||||||
мальным вектором плоскости. |
|
|
|
|
|
||
|
N |
Пусть для данной плоскости известен нор- |
|||||
|
мальный вектор |
N =(A, B, C) |
и |
точка |
|||
|
|
||||||
|
|
M0 (x0 , y0 , z0 ), лежащая на плоскости. |
|
|
|||
M |
|
Пусть также M (x, y, z) |
произвольная точка |
||||
|
|
|
|
|
|
|
|
M0 |
|
плоскости. |
Тогда |
|
M0M N , |
где |
|
РИС. 3.2.1 |
|
M0M =(x − x0, y − y0 , z − z0 ). |
|
|
|
||
Записав условие перпендикулярности векторов, получим уравнение плоскости
A(x − x0 )+ B (y − y0 )+ C (z − z0 )= 0 ,
которое называется уравнением плоскости, проходящей через точку M0 (x0 , y0 , z0 ) с данным нормальным вектором N =(A, B, C).
2) Так же, как для прямой на плоскости можно записать общее уравне-
ние плоскости:
Ax + By +Cz + D =0, (A2 + B2 + C2 ≠ 0).
41
3.2.1.2. Уравнение прямой в пространстве
1. Любую прямую в пространстве можно рассматривать как линию пересечения двух плоскостей, если они не параллельны. Поэтому система двух уравнений
A1x + B1 y + C1z + D1 = 0A2 x + B2 y + C2 z + D2 = 0
задает прямую в пространстве и называется общими уравнениями прямой в пространстве.
2. При решении задач на прямую в пространстве чаще используют другой
способ задания. |
|
|
|
|
|
|
|
|
|
|
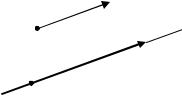
Пусть S =(m, n, p) |
- направляющий, вектор прямой (лежащий на прямой |
|||||||||
или параллельной ей) и M0 (x0 , y0 , z0 ) - данная точка на прямой. |
||||||||||
|
Пусть M (x, |
y, z) – произвольная точка на прямой, то- |
||||||||
S |
гда векторы |
M0M =(x − x0 , y − y0 , z − z0 ) и S колли- |
||||||||
|
неарны. |
|
|
|
|
|
|
|
|
|
M |
Записывая условие коллинеарности векторов, получим |
|||||||||
|
||||||||||
M0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x − x0 |
= |
y − y0 |
= |
z − z0 |
|
. |
|
|
|
|
|
|
||||||
РИС. 3.2.2 |
|
|
|
m |
n |
p |
||||
|
|
|
|
|
|
|||||
Отметим основные свойства уравнений прямой в пространстве:
1)количество уравнений – 2;
2)уравнения линейные, т.е. содержат переменные в первой степени с числовыми коэффициентами.
3.2.2. Основные задачи аналитической геометрии на плоскости
Рассмотрим основные задачи, связанные с уравнением прямой на плоскости в 2 .
1) Проверить принадлежности точки M0 (x0 , y0 ) прямой
Ax + By +C =0.
Если координаты точки M 0 удовлетворяют уравнению прямой
Ax0 + By0 + C = 0
42
то точка лежит на прямой.
2) Найти точку пересечения прямых
A1x + B1 y + C = 0, A2 x + B2 y + C2 = 0
Для этого решаем систему линейных уравнений
A1x + B1 y = −C1A2 x + B2 y = −C2
Если эта система имеет единственное решение (x0 , y0 ), то точка
M (x0 , y0 ) является точкой пересечения прямых.
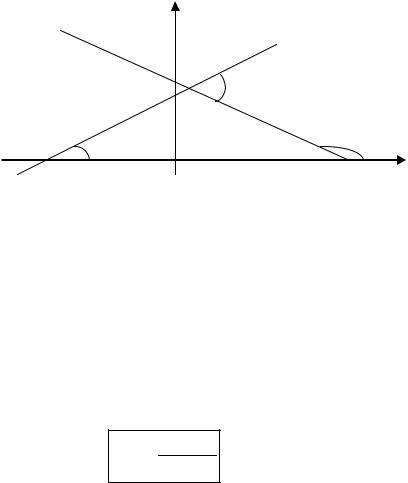
3) Найти угол ϕ между прямыми. При вычислении мы можем найти острый угол ϕ или дополнительный к нему тупой угол π − ϕ.
l2 |
y |
|
l1 |
ϕ
α1 |
|
|
|
|
|
α2 x |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
Для вычисления ϕ получим несколько формул, используемые в зависи- |
||||||
мости от уравнения прямых. |
|
|
|
|
|
|
а) Прямые: y = k1x + b1, y = k2 x + b2 |
|
|||||
Так как α1 + ϕ = α2 , то ϕ = α2 − α1. Отсюда |
|
|||||
tg ϕ = tg(α |
2 |
− α |
)= |
tg α2 − tg α1 |
, |
|
|
||||||
|
1 |
|
1 + tg α2 tg α1 |
|
||
|
|
|
|
|
||
а так как tg α1 = k1, tg α2 = k2 , то
tg ϕ = k2 − k1
1 + k1k2
б) Прямые имеют направляющие векторы S1 =(m1,n1 ), S2 =(m2 ,n2 ).
Тогда ϕ=(S1, S2 ), а значит
43
cosϕ= cos(S1, S2 )= S1 S2
S1 S2
или
cosϕ = |
m1m2 + n1n2 |
|
|||
m2 |
+ n2 |
m2 |
+ n2 |
|
|
|
|
||||
|
1 |
1 |
2 |
2 |
|
в) Прямые имеют нормальные векторы N1 =(A1, B1 ), N2 =(A2 , B2 ).
Тогда ϕ=(N1, N2 ), а значит
cosϕ= cos(N1, N2 )= N1 N2
N1 N2
или
cosϕ = |
A1 A2 + B1B2 |
|
|||
A2 |
+ B2 |
A2 |
+ B2 |
|
|
|
|
||||
|
1 |
1 |
2 |
2 |
|
4) Условие параллельности двух прямых. Прямые параллельны l1 l2
а) S |
S |
2 |
|
|
m1 |
= |
n1 |
|
|||
|
|
|
|
|
|||||||
1 |
|
|
|
m2 |
|
n2 |
|||||
|
|
|
|
|
|
||||||
б) N |
N |
2 |
|
A1 |
= |
B1 |
|||||
|
|
||||||||||
1 |
|
|
|
|
A2 |
|
|
B2 |
|||
|
|
|
|
|
|
|
|
||||
в) ϕ = 0, tgϕ = 0 k1 = k2 .
5) Условие перпендикулярности двух прямых.
Прямые перпендикулярны l1 l2
а) S1 S2 m1m2 + n1n2 = 0 б) N1 N2 A1 A2 + B1B2 = 0
в) ϕ = π tgϕ − не существует 1 + k k |
2 |
= 0 k k |
2 |
= −1. |
|
2 |
1 |
1 |
|
||
|
|
|
|
|
|
3.3. Кривые второго порядка |
|
|
|
|
|
Линией второго порядка на плоскости |
|
2 |
называется множество точек, |
||
координаты которых удовлетворяют уравнению второй степени
44
Ax2 + Bxy +Cy2 + Dx + Ey + F =0 . |
(20) |
Изучим свойства, построим графики линий второго порядка.
3.3.1. Окружность
Окружность – линия второго порядка, каноническое уравнение которой имеет вид
x2 + y2 = R2 .
Окружность – хорошо известная из школы кривая, которая определялась как множество точек на плоскости, равноудаленных от точки, называемой центром окружности. Расстояние от центра до точек окружности называется ради-
усом.
Для окружности, имеющей уравнение
x2 + y2 = R2
центр находится в точке O (0,0), а радиус – R .
Если центр окружности находится в точке M (x0 , y0 ) , а радиус R , то уравнение окружности имеет вид (x − x0 )2 + (y − y0 )2 = R2 .
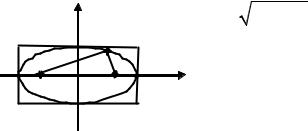
3.3.2. Эллипс
Эллипс – линия второго порядка, каноническое уравнение которой имеет
вид
|
|
|
|
|
|
x2 |
+ |
y2 |
=1 |
|
|
|
|
|
|
|
|
|
|
a2 |
b2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
График |
|
эллипса |
|
Числа a,b – полуоси эллипса. |
|
|||||||
имеет вид |
|
|
|
|
Если |
|
a ≥ b , |
можно |
ввести |
число |
|||
|
y |
|
|
c = |
|
a2 −b2 < a . Точки F (−c,0), |
F (c,0) называют |
||||||
|
b B2 |
M |
|
|
|
|
|
|
|
|
1 |
2 |
|
|
A2 |
фокусами эллипса. |
|
|
|
||||||||
A |
r1 |
r |
|
|
|
||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
F2 |
|
|
|
|
|
|
M (x, y) |
|
|
|
|
-a F1 О |
a |
x |
|
Если |
– произвольная точка эллипса, |
||||||||
|
-b B1 |
|
|
то |
длины |
отрезков |
MF1 = r1, MF2 = r2 называются |
||||||
|
|
|
|
||||||||||
|
РИС. 3.3.1 |
фокальными расстояниями точки M . |
|
||||||||||
|
|
|
|
|
|||||||||
45
Основное свойство эллипса (фокальное свойство): для любой точки эллипса r1 + r2 = 2a (сумма фокальных расстояний равна большой оси).
Замечание. Если b ≥ a , то фокусы лежат на оси 0y и основное свойство
примет вид: r1 + r2 = 2b .
Эксцентриситетом эллипса называется число ε = ac . Для эллипса ε <1 (для окружности a =b c = 0 ε = 0 ).
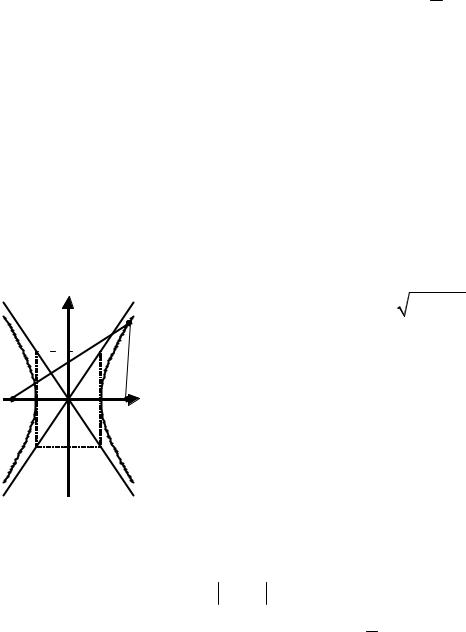
3.3.3. Гипербола
Гипербола – это линия второго порядка, каноническое уравнение которой имеет вид
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
− |
y2 |
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
b2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
График гиперболы имеет |
a – действительная полуось, b – мнимая полу- |
||||||||||||||||||||
|
|
|
|
|
вид |
|
ось. |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
y |
M |
|
|
Введем число c = |
a |
2 |
+b |
2 |
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
b |
|
|
Точки F1 (−c,0), |
F2 (c,0) - называются фо- |
||||||||||||
|
|
|
r1 |
|
r2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
кусами гиперболы. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
-а |
|
|
|
A2 |
|
|
|
|
|
||||||||||||
F1 A1 |
|
О a |
F2x |
|
|
Если M (x, y) - произвольная точка гипер- |
|||||||||||||||
|
|
|
|
|
-b |
|
болы, |
то длины отрезков: |
MF1 = r1 , MF2 = r2 - |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
называются фокальными расстояниями. |
|||||||||
РИС. 3.3.2
Основное (фокальное) свойство гиперболы: r1 − r2 = 2a .
Эксцентриситет гиперболы – это число ε= ac >1.
3.3.4. Парабола
Парабола – это линия второго порядка, каноническое уравнение которой имеет вид
y2 = 2 px . 46
|
|
d |
y |
|
Точка F |
p |
,0 называется фокусом параболы, а |
||||
|
|
|
|
M |
|
|
|||||
|
|
|
|
|
|
|
|
2 |
|
||
|
|
|
|
|
r |
|
|
p |
|
|
|
|
|
O |
|
F |
|
|
|
||||
|
|
|
x |
прямая x = − 2 называется директрисой параболы. Пусть |
|||||||
− |
p |
|
p |
||||||||
|
|
|
|
|
|
M (x, y) - производная точка параболы. |
|||||
2 |
|
2 |
|
|
|||||||
РИС. 3.3.3
Основное свойство параболы: расстояние от любой точки M параболы до фокуса и до директрисы одинаковы: MF = MN r = d .
Эксцентриситет параболы равен единице: ε =1.
47
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
Математика: Учебник для студентов вузов, обучающихся по специальностям экономики и управления (060000) / Б.Т. Кузнецов – 2-е изд., перераб. и доп. – М: ЮНИТИ-ДАНА, 2012. – 719 с. – (Серия «Высшее профессиональное образование: Экономика и управление»).
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
а) основная литература
Высшая математика для экономистов: учебник для студентов вузов, обучающихся по экономическим специальностям / [Н.Ш. Кремер и др.]; под ред. проф. H . Ш. Кремера. – 3-е изд. – М.: ЮНИТИ-ДАНА, 2012. – 479 с. – (Серия «Золотой фонд российских учебников»)
Кузнецов Б.Т. Математика : Учебник для студентов вузов, обучающихся по специальностям экономики и управления (060000) / Б.Т. Кузнецов. – 2-е изд., перераб. и доп . – М.: ЮНИТИ-ДАНА, 2012. – 719 с. – (Серия «Высшее профессиональное образование: Экономика и управление»).
Бурмистрова Е.Б. Математический анализ и дифференциальные уравнения: учеб. / Е.Б. Бурмистрова, С.Г. Лобанов. – М.: Изд. Центр "Академия", 2010.
– 368 с.
Бурмистрова Е.Б. Линейная алгебра, дифференциальное исчисление функций одной переменной: учеб. / Е.Б. Бурмистрова, С.Г. Лобанов. - М.: Изд. Центр "Академия", 2010. - 336 с.
Сборник задач по высшей математике для экономистов: Учебное пособие / Под ред. В.И. Ермакова. – ИНФРА-М, 2007. – 575 с. (Серия «Высшее образование»).
Протасов Ю. М. Математический анализ. Учебное пособие. – М.: Издательство «ФЛИНТА», 2012. – 165 с. – Университетская библиотека онлайн.
Геворкян П. С. Высшая математика. Линейная алгебра и аналитическая геометрия. – М.: Физматлит, 2011. – 207 с. – Университетская библиотека онлайн.
48
б) дополнительная литература
Математика для экономистов: электронный учебник / С.И. Макаров. - М.: КНОРУС, 2009. – Электронный опт. диск.
Математика для экономистов: уч. пособ. / С.И. Макаров. – 2-е изд., стер. –
М.: КНОРУС, 2008. – 264 с.
Красс М.С. Математика для экономического бакалавриата: учеб. / М.С. Красс, Б.П. Чупрынов. – М.: ИНФРА-М, 2012. – 472 с.
Математика для экономистов. Задачник: уч.-практ. пособ. / под ред. С.И. Макарова, М.В. Мищенко. – М.: КНОРУС, 2008. – 360 с.
Математическое моделирование в экономике: учебное пособие/В.И. Мажукин, О.Н. Королева – М.: Изд-во «Флинта», Московский гуманитарный уни-
верситет, 2004. – 232 с.
Шапкин А. С. Шапкин В. А. Математические методы и модели исследования операций. Учебник. – 5-е изд. – М.: Дашков и Ко, 2012. – 397 с. – Университетская библиотека онлайн.
Баврин И.И. Высшая математика. – М. AKADEMA, 2004. – 611с. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.
Высшая школа, 2003. – 479 с.
Шипачев В.С. Высшая математика. – М. Высшая школа, 2005. – 479с. Шипачев В.С. Задачник по высшей математике. – М. Высшая школа,
2004. – 304с.
Математическое программирование в примерах и задачах. /И.Л. Акулич. – М.: Высшая школа, 1986. – 319 с.
Задачи и модели исследования операций: Учебное пособие в 3-х частях/ С.И. Жогаль, И.В. Максимей – Гомель: БелГУТ, 1999. Ч.1 Аналитические модели исследования операций. – 110 с.
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: Учеб. пособие для студентов втузов. В двух частях. Часть I. – 4-е изд.испр. и доп. – М.: Высш. шк., 1986. – 304 с., ил.
49
